

Seminar und Übung
- Physikalische Prozesse in der Ökologie -
Die Nettophotosynthese der Blätter liefert Kohlenhydrate für Wachstum und Erhalt der Waldbäume. In diesem Kurs werden fundamentale Beziehungen angesprochen, die die Netto-Photosynthese von Baumkronen und Kronenschichten steuern. Es werden folgende Themen behandelt:
Die photosynthetisch aktive Strahlung (PAR)
Entsprechend der photochemischen Prozesse bei der Photosynthese wirken vom Blatt absorbierte Photonen innerhalb des Wellenlängenbereiches 400 - 700 nm unabhängig ihres Energiegehaltes, d.h. überschüssige Energie wird über Fluoreszenz abgestrahlt oder führt zur Erwärmung des Blattes. Daher ist es sinnvoll, die Photonenflussdichte (FPAR im englischen auch PPFD, Einheit [µE/(m² s)]) und nicht den Energiegehalt der ankommenden Strahlung zu messen. Dieses wird mit einem PAR-Sensor mittels Filtern dadurch erreicht, dass energiereichere (= kürzere) Wellenlängen entsprechend stärker herab gewichtet werden (Abb. 1). Eine andere Bezeichnung für den PAR-Sensor ist deshalb auch "Lichtquantenzähler" (quantum sensor). Das PAR-Konzept hat in der Pflanzenökophysiologie das Lichtkonzept LUX abgelöst. Die Einheit µE (mikro Einstein) entspricht 10-6 mol Photonen. Sie haben in der Übung 3 bereits ausgerechnet, wie groß der Anteil des PAR-Bereiches an der Globalstrahlung in Energieeinheiten ist. Näherungsweise gilt für Strahlung außerhalb von Baumkronen FPAR ca. = 2·G · µE/(m²·s) · (W/m²)-1.

Abb. 1: Spektrale Filterung der kurzwelligen Strahlung des PAR-Sensors (LI-190, Fa. LI-COR, Lincoln, USA)
Die photosynthetisch nutzbare Strahlung (PUR)
Messungen der Photosyntheseleistung von Blättern in Abhängigkeit vom Spektrum der einfallenden Strahlung zeigten jedoch, dass die Photosyntheseaktivität nicht über den gesamten Wellenbereich des Lichtes konstant ist, sondern vielmehr im Grünbereich (550 nm) ein Minimum aufweist (Abb. 2). Hier ist die Absorption des (grünen!) Chlorophylls minimal. Dies ist von besonderer Bedeutung, weil in diesen Wellenlängenbereich das Intensitätsmaximum der Globalstrahlung fällt. Der PUR-Sensor soll die einfallende Strahlung so wichten, wie es der mittleren spektralen Empfindlichkeit der Photo-synthese grüner Pflanzen entspricht. Die PUR-Strahlung wird hier in Energiestromdichte (W/m²) wie z.B. bei der Globalstrahlung und bei der Strahlungsbilanz angegeben.
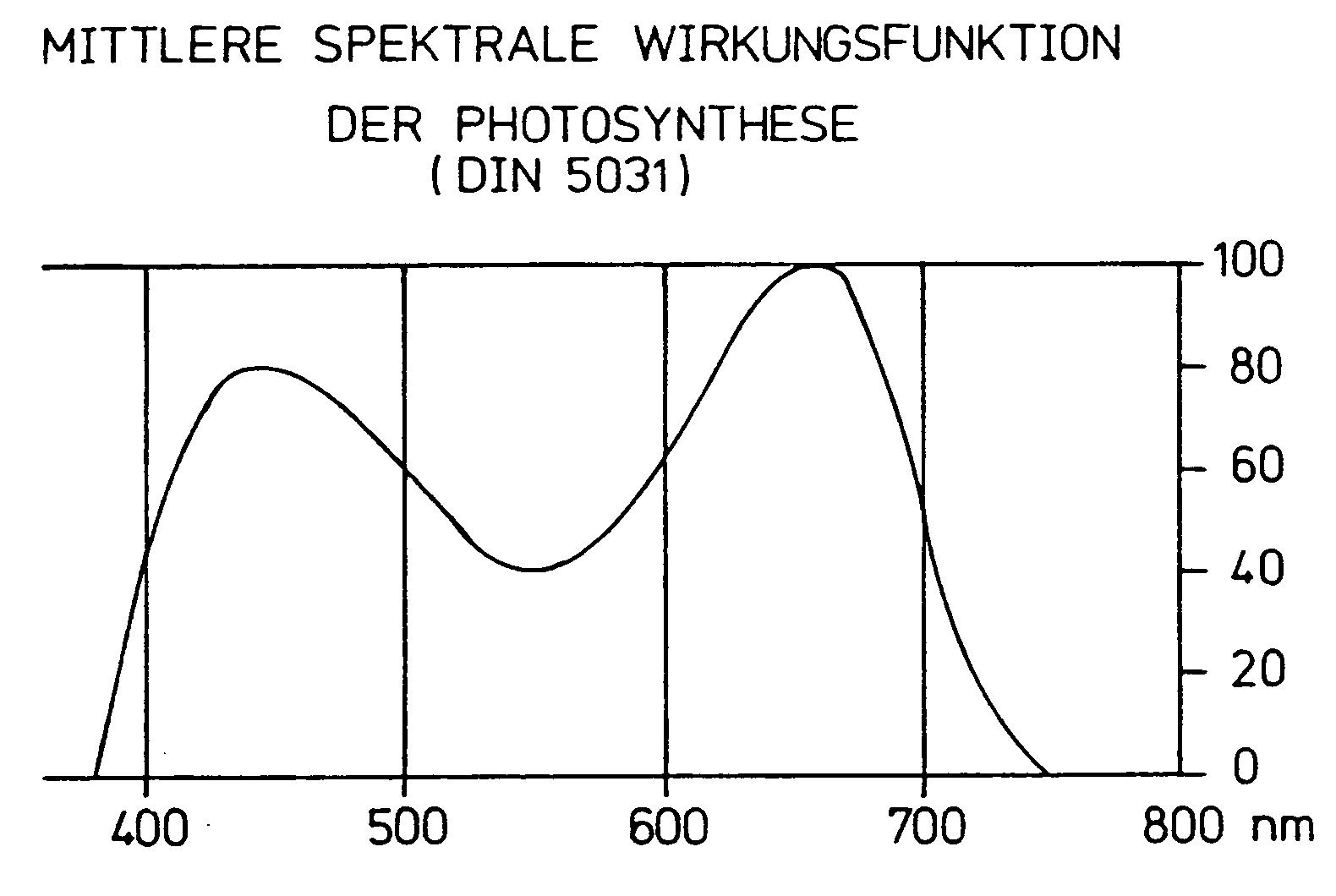
Abb. 2: Die mittlere spektrale Wirkungsfunktion der Photosynthese.
Die wissenschaftliche Entwicklung der letzen 30 Jahre
hat die wesentlichen Grundlagen der Steuerung der Photosynthese- und
Blattgaswechselraten aufgedeckt. Diese Grundlagen sollen hier
nicht behandelt werden. Wir werden uns nur mit ihrer
Lichtabhängigkeit und das nicht kausal sondern nur
phänomenologisch beschäftigen.
Thornley beschrieb das Sättigungsverhalten der Brutto-Photosynthese GPR in Abhängigkeit von der Photonenflussdichte I mit der nicht rechtwinkligen Hyperbel:
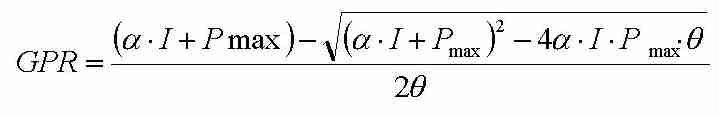 (Gl. 1)
(Gl. 1)mit den Parametern a:
Lichtausnutzungseffizienz, Pmax: maximale Photosyntheserate und
q: Parameter für die Krümmung der
Hyperbel. Die Form dieser Funktion ist in Abb. 3 dargestellt.
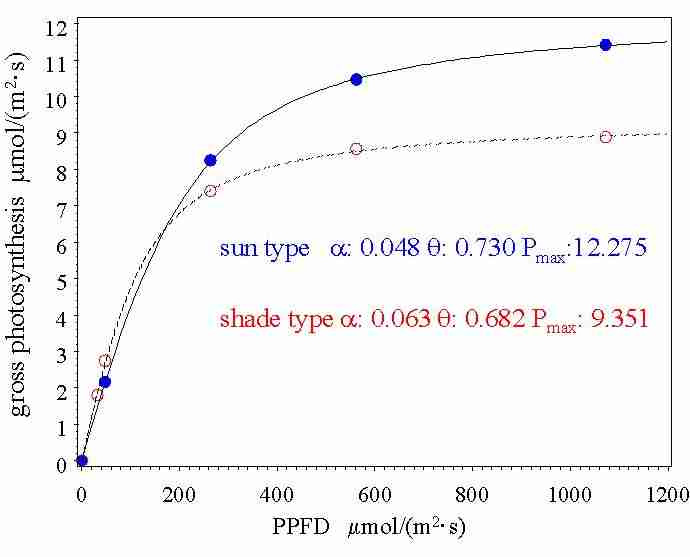
Abb. 3: Lichtabhängigkeit der
Bruttophotosyntheserate von Sitkafichtenzweigen (Leverenz und Jarvis,
1983).
Die Nettophotosynthese NPR ergibt sich durch Berücksichtigung der Atmungsrate Rd nach
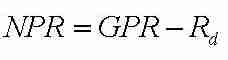 . (Gl. 2)
. (Gl. 2)
Interaktion zwischen Blättern und Strahlung und
optische Blatteigenschaften
Blätter wechselwirken auf verschiedene Weise mit der kurzwelligen Strahlung. Dabei ergeben sich sowohl spektrale Intensitätsunterschiede als auch Richtungsänderungen der Strahlung (Abb. 4 und Abb. 5).
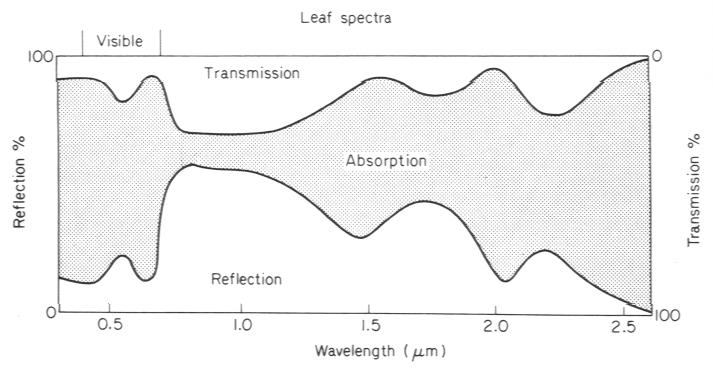
Abb. 4: Reflexion, Transmission und Absorption eines Blattes (generalisiert, nach Monteith und Unsworth, 1990).Diese optischen Blatteigenschaften wollen wir mit τ für die Transmission, α für die Absorption und ρ für die Reflexion bezeichnen (Achtung: Absorption nicht mit der Lichtausnutzungseffizienz verwechseln).
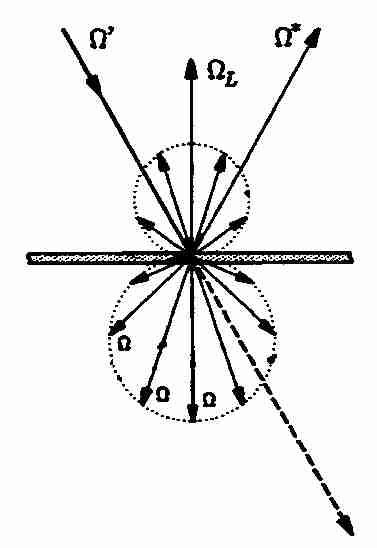
Abb. 5: Richtungsabhängigkeit der Streuung (nach Kranigk, 1994)Die Berücksichtigung all dieser Einflussgrößen mach die Simulation der Strahlung in Kronenräumen numerisch extrem kompliziert und bisher nur für Spezialisten mit dem nötigen mathematischen Background möglich.
Es kann jedoch für unsere Zwecke nach geeigneten Näherungen gesucht werden. Ein erster Schritt ist der, von isotroper Streuung auszugehen (ρ=τ) und die spezielle Richtungsabhängigkeit dann nur in zwei Richtungen zu betrachten (1D-Ansatz), bzw. noch stärker vereinfacht die Blätter in erster Näherung als schwarz anzusehen (ρ=τ=0 und α=1). Wie in Tab. 1 zu erkennen ist, werden damit die optischen Eigenschaften von Fichtennadeln im PAR-Bereich gut angenähert.
| Prozess | VIS (=PAR) | NIR |
| Absorption | 90 | 41 |
| Reflexion | 7 | 26 |
| Transmission | 3 | 33 |
Die Blattskale
Es ist unmittelbar einsehbar, dass die Strahlung nur mit dem Teil der Oberfläche wechselwirkt, der der Strahlungsquelle zugewand ist. Mathematisch gesprochen, heißt diese Fläche die senkrecht zur Strahlungsausbreitungsrichtung projizierte Fläche. Abb. 6 stellt diesen Zusammenhang am Beispiel eines Kollektives von Buchenblättern dar.
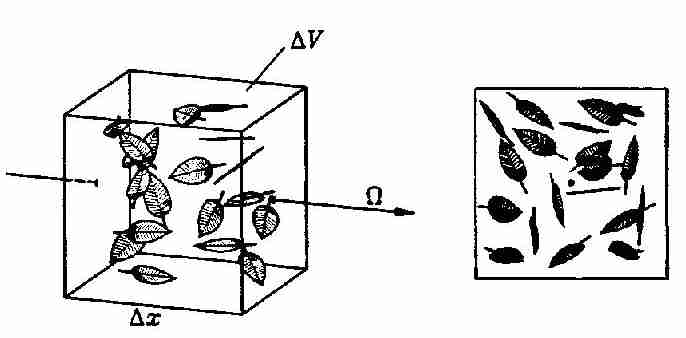
Abb. 6: Ein Kollektiv von Buchenblättern in einem
Volumenelement und ihre projizierte Fläche senkrecht zur
Strahlrichtung Ω (aus Kranigk, 1994).
Die projizierte Fläche Ap ist in der Regel
kleiner als die selten gleich der Gesamtfläche A. Das
Verhältnis Ap/A
wird bei senkrechter Sonneneinstrahlung als Extinktionskoeffizient k
bezeichnet. k
ist eine
Funktion der Blattstellungswinkelverteilung. Wenn wir uns die
verschiedenen
Formen vorstellen, die die Artenvielfalt von Waldbäumen
hervorgebracht
hat, stellen wir leicht fest: Die Blattstellungswinkel sind keineswegs
konstant! Vielmehr variieren sie sowohl in azimutaler Richtung
(Kompassrichtung) als auch in vertikaler Richtung. Häufig reicht
es aus, die azimutale Verteilung der Blattstellungswinkel als
gleichverteilt anzunehmen (jede Richtung kommt mit der gleichen
Wahrscheinlichkeit vor). In der vertikalen Winkelverteilung kommt es
jedoch zu charakteristischen Unterschieden sowohl zwischen
verschiedenen Arten als auch innerhalb der Blattkollektive bestimmter
Kronenbereiche mancher Baumarten (Sonn- Schattenmodifikation).
Für die Strahlungsverteilung in Medien von
schwarzen Blättern hat k eine ganz einfache Konsequenz.
Die Strahlungsabschwächung in einer Schicht ist proportional zu
Ap. Die Strahlungsabschwächung
pro Blattfläche ist dann
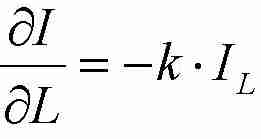 (Gl. 3),
(Gl. 3),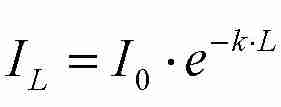 (Gl. 4)
(Gl. 4)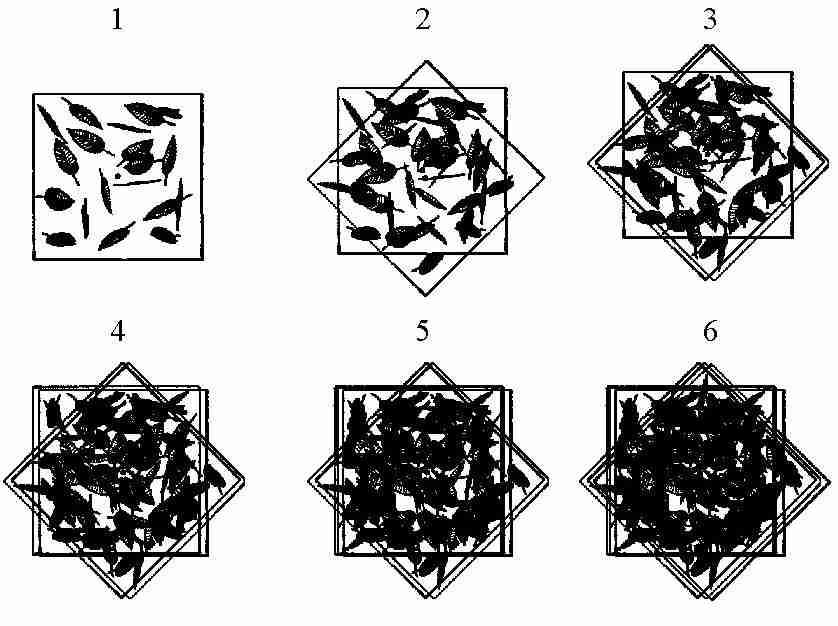
Abb. 7: Überlagerung der Projektionen eines
Blattkollektivs.
Die Blattwinkelverteilungen lassen sich einfach anhand der Oberflächen geometrischer Körper darstellen. Denn, ordnet man die Blattstellungswinkel nach Azimut- und Vertikalwinkel, so kann man daraus Oberflächen einfacher, geometrischer Figuren konstruieren. Unter der Annahme, dass alle Azimutwinkel gleichverteilt sind, bilden senkrecht angeordnete Blätter einen Zylinder, horizontal angeordnete Blätter eine Ebene. Ist neben dem Azimutwinkel auch der Vertikalwinkel gleichverteilt, so lässt sich aus den Blättern eine Kugeloberfläche konstruieren. Eine solche Verteilung heißt sphärisch. Übergänge zwischen senkrechter und sphärischer Verteilung , wir sagen erectophile Winkelverteilung, lassen sich mit einem Ellipsoid, der rotationssymmetrisch zur Vertikalen ist, und dessen Länge a in senkrechter Richtung die von b in horizontaler Richtung überschreitet. Herrschen horizontale Blattstellungen vor, spricht man von einer planophilen Verteilung (Abb. 8).
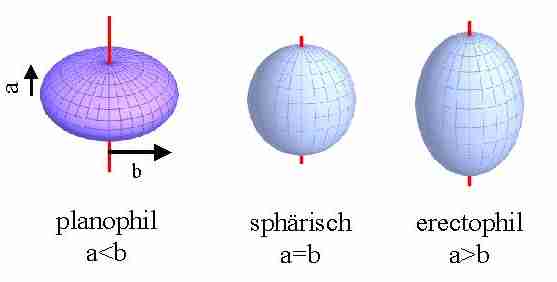
Abb. 8: Geometrische Repräsentation von
Blattstellungswinkelverteilungen (Ellipsoide aus http://www.geometrie.tuwien.ac.at/student/arch/).
Wir kennen alle Übergänge von planophilen (z.B. Helianthus annuus oder die Schattenblätter von Fagus silvatica) bis hin zu erectophilen (Gladiolus, Allium) Blattwinkelverteilungen. Die Nadeloberfläche vieler Koniferen (z.B. Picea abies) ist mit guter Näherung sphärisch.
Wie sich die geometrischen Oberflächen auf verschieden Ebenen projizieren, veranschaulicht Abb. 8 am Beispiel der sphärischen Verteilung.
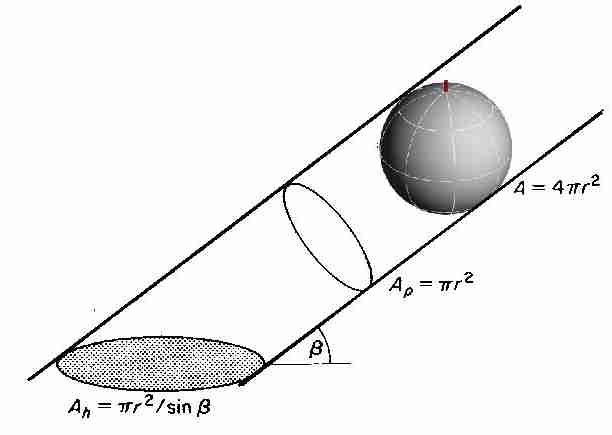
Abb. 9: Projektion der Kugeloberfläche senkrecht
zur Strahlungsrichtung (Ap) und auf die Horizontale (Ah)
aus Monteith und Unsworth (1990).
Ap/A der Kugel ist demnach gleich 0,25
und Ah/A der
Kugel gleich 0,25/sin(β). Die
Projektion wird jedoch nur von einer Hälfte der
Kugeloberfläche beeinflusst, denn die
untere Hälfte der Kugeloberfläche wird von der Oberseite
vollständig beschattet. Hier liegen die
Grenzen
unserer Analogie, da wir die betrachtete Schicht ja so klein
gewählt
haben, dass Selbstbeschattung vernachlässigt werden kann. Demnach
müssen
wir Oberseite und Unterseite der Kugeloberfläche jeweils getrennt
betrachten.
Für die sphärische Verteilung gilt bei senkrechter
Sonneneinstrahlung: ksp=Ap/A=2·0,25=0,5!
Das Verhältnis der Projektionsfläche auf die horizontale
Ebene
zur Gesamtfläche (Ah/A) hängt vom
Inklinationswinkel der Sonne, hier
β,
ab. Dies haben wir schon bei der
Richtungsabhängigkeit der Strahlungsflussdichte kennengelernt . Wie dieser in Abhängigkeit von Ort und Zeit auf der
Erdoberfläche
zu berechnen ist, haben Sie am Beispiel der Berechnung der potenziellen
Globalstrahlung
kennengelernt (vgl. Strahlung
I: Strahlungsgesetze, Achtung: Dort wird
β als ψ bezeichnet!).
In Abb. 10 sind Beispiele für
Extinktionskoeffizienten, nun ksp=Ah/A=0,5/cos(θ), verschiedener
Blattstellungswinkelverteilungen
in Abhängigkeit von
dem Inklinationswinkel der Sonne dargestellt. Mit diesen Werten und dem
Lambert Beer'schen Gesetz (Gl. 4) können Sie nun die
Strahlungsverteilung in einem homogenen Medium aus schwarzen
Blättern berechnen.
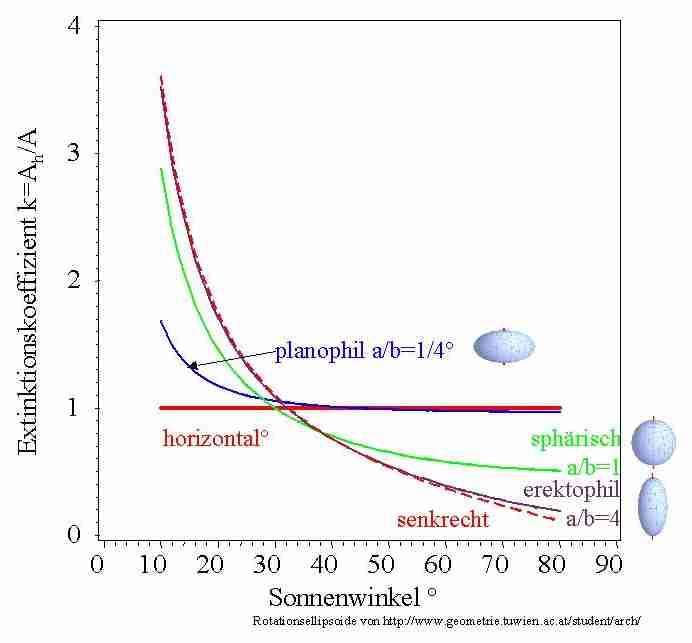
Abb. 10: Beispiele von Extinktionskoeffizienten bei
unterschiedlichem Sonnenvertikalwinkel und
Blattstellungswinkelverteilung.
Effekte der Struktur auf die Strahlungsverteilung auf höheren räumlichen Skalen
In der Realität genügen Baumkronen nur sehr selten dem Kriterium der Homogenität. Die Auswirkungen verdeutlicht Abb. 11.
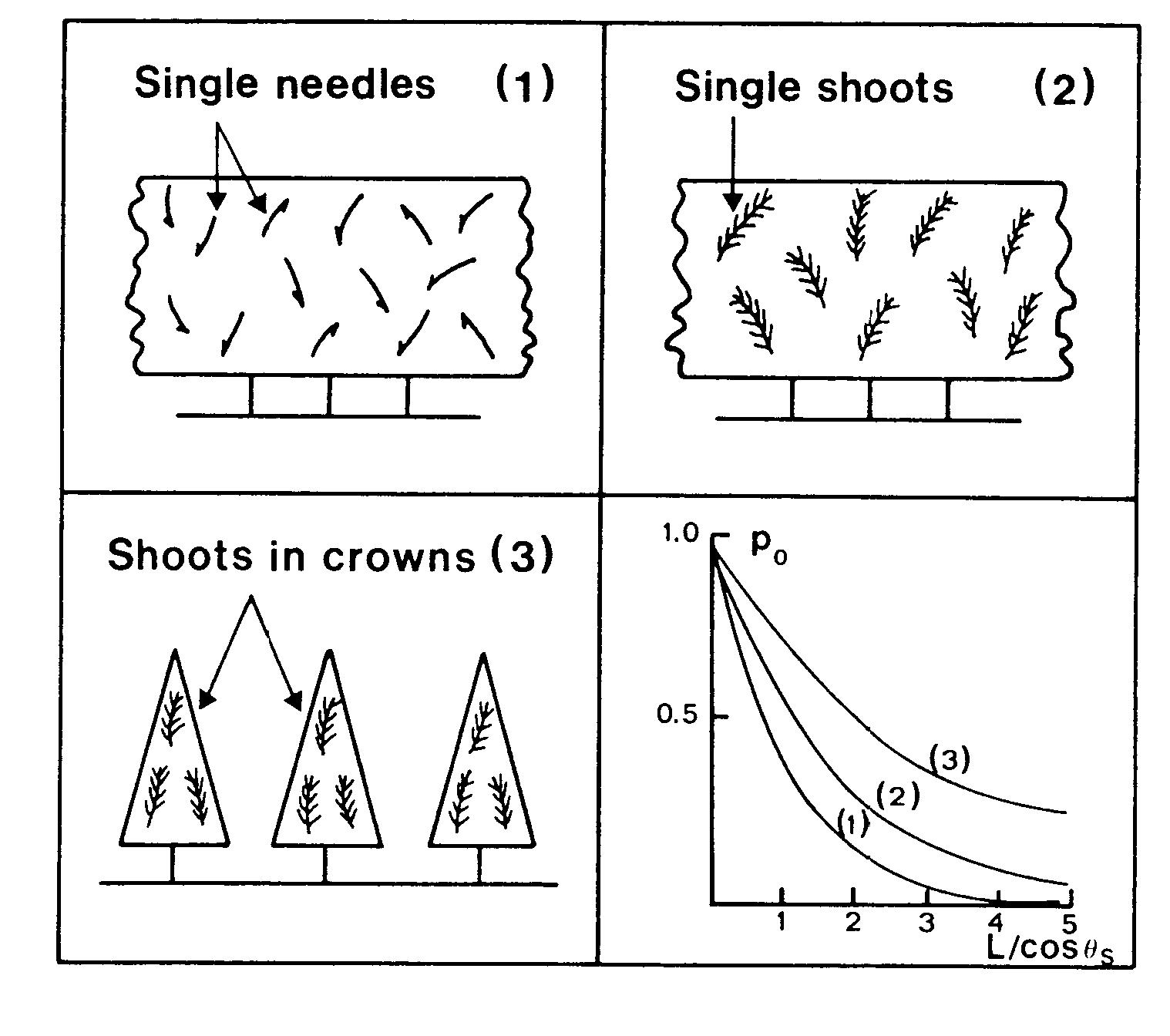
Wir erkennen, dass je stärker der Grad der
Klumpung ist, desto weniger Strahlung wird bei gleichem
Blattflächenindex von dem Kronendach absorbiert, bzw.
desto
mehr Strahlung wird zum Boden transmittiert. Interessanterweise
kann man beobachten, dass die Blattfläche von relativ geklumpt
angeordneten Kronenräumen i.d.R. höhere Blattflächen
aufwiesen als solche mit homogener Verteilung. Dies ist ein Beispiel
für eine Struktur-Funktionsbeziehung, die zu Zugang zum Verstehen
des komplexen Systems Einzelbaum - Baumbestand in seiner Umwelt
vermittelt.
Ist die PAR-Flussdichte bekannt, kann die Photosynthese einfach mit den Gleichungen 1 und 2 berechnet werden. Jedoch ist zu berücksichtigen, dass die Strahlungsflussdichte vom Winkel des Blattes zur Strahlungsrichtung abhängt. Die einfache Mittelung und anschließende Berechnung der Photosynthese ist wegen der Nicht-Linearität von Gl. 1 nicht erlaubt. Daher muss die Photosynthese für einzelne Klassen der Blattwinkelverteilung gesondert berechnet und über die Blattfläche einer Schicht integriert werden.