

- Physikalische Prozesse in der
Ökologie -
Unter Verdunstung versteht man die Phasenumwandlung von flüssigem Wasser in Wasserdampf. Sie ist ein entscheidender Prozess sowohl für den physikalischen Zustand der Atmosphäre (Wetter, Klima) als auch für die Wasserversorgung von Ökosystemen (Pflanzen, Boden).
Ist die Atmosphäre auch nur wenige Prozente
untersättigt, verdunsten feuchte Oberflächen flüssiges
Wasser. Unter Kondensation versteht man die Umkehrung der Verdunstung.
Die Richtung des Transportes hängt von dem Vorzeichen der
Differenz der chemischen Potenziale zwischen Ausgangs- und Endzustand
des Wassers ab, d.h., z.B. als Flüssigwasser in
Lösungen wie Oberflächengewässer,
Apoplastenlösung in den Zellwänden von Blättern
oder Bodenlösung, oder in Form von Wasserdampf in der
Atmosphäre. Im ökologischen Bereich sind wir gewohnt, das chemische
Potenzial des Wassers auch einfach als Wasserpotenzial Ψ, die Differenz vom unter Spannung befindlichen Wasser zum
freien Wasser, zu bezeichnen. Diese Differenz ist negativ und wird als
Druck (=Energie / Volumen) in der Einheit Pa angegeben.
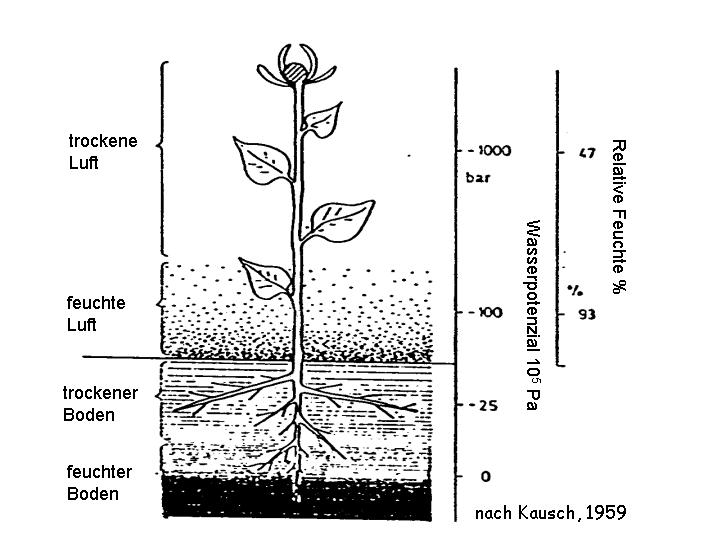
Das chemische Potenzial des Wassers hängt eng mit
der relativen Feuchte zusammen. Bereits wenige %
Untersättigung der Atmosphäre bedeuten schon ein sehr stark
negatives chemisches Potenzial von einigen MPa, also viel höher
als das in der Wurzelzone des Bodens oder auch im pflanzlichen Gewebe.
Im Gleichgewichtsendpunkt ist die Änderung des chemischen
Potenzials gleich Null. Die Atmosphäre erreicht dieses
Gleichgewicht jedoch i.d.R. nicht. Durch Ausregnen bleibt die
Atmosphäre in der Regel m.o.w. stark untersättigt.
Die Flussdichte des Wasserdampfes von
einer Wasseroberfläche E (Evaporationsrate = Rate der
Wasserdampfabgabe pro Quadratmeter pro Zeit) bestimmt jedoch nicht die
Differenz des chemischen Potenzials, sondern die Differenz des
Wasserdampfpartialdruckes zwischen
der Oberfläche und einer Referenzhöhe und die
Leitfähigkeit
der Atmosphäre (g=1/r). Die folgenden Überlegungen
sollen
ihnen das Verständnis für die Steuerung und die quantitative
Beschreibung der Verdunstung vermitteln.
Allgemein gilt für die Verdunstungsrate (Wasserdampfflussdichte)
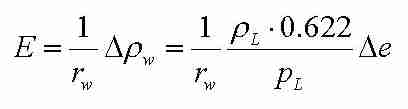 (Gl. 1)
(Gl. 1) (Gl. 1b),
(Gl. 1b),Die Verdunstung von Wasser ist nicht nur ein Stoff- sondern auch ein Energiefluss. Die Energiemenge, die für die Verdunstung verbraucht wird, ist das Produkt aus Verdunstung und Verdampfungswärme λw, oder hier einfach λ, also gilt
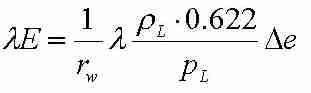 . (Gl. 2)
. (Gl. 2)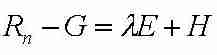 (Gl. 3).
(Gl. 3).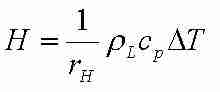 (Gl. 4),
(Gl. 4),
Vorbereitend zur komplizierten Situation im Baumbestand betrachten wir nun die beiden Thermometer eines Psychrometers. Das Psychrometer ist ein leicht verständliches Modell einer adiabatischen Zustandsänderung, bei der Energieflüsse zwischen der Luft und der Oberfläche (Feucht- oder Trockenthermometer) vorkommen können.
Stellen Sie für die folgenden Situationen die Gleichung 3 auf und charakterisieren sie ihre Terme in ihrer Beziehung zu Null (>, = oder < 0).
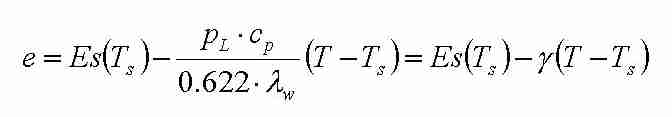 (Gl. 8)
(Gl. 8)Diese Gleichung wird zur Berechnung des aktuellen
Dampfdruckes aus der Temperaturdifferenz zwischen Trocken- und
Feuchtthermometer eines Psychrometers nach Einstellung des
Gleichgewichtes verwendet. Uns besagt sie etwas darüber, in
welchem Maße im adiabatischen Fall durch Verdunstung die
Temperatur an der Oberfläche absinkt und dabei der
aktuelle Dampfdruck zunimmt.
Mit γ
wird die Psychrometerkonstante bezeichnet, sie nimmt bei 20
°C einen Wert von 66 Pa/K an.
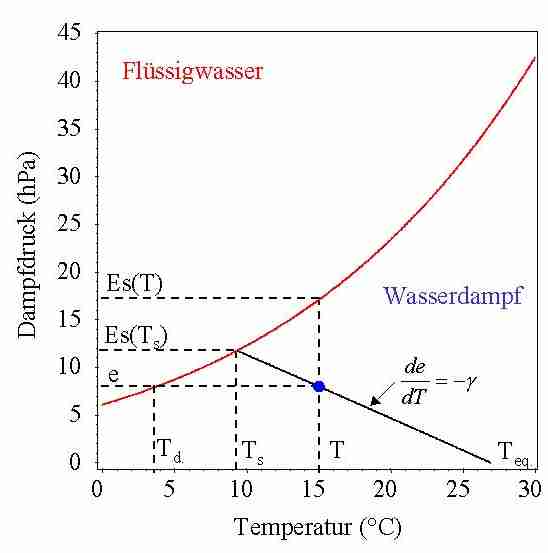
Lassen wir nun Strahlung zu und behandeln damit den
allgemeingültigeren, diabatischen Fall, wie er in der
Natur die Regel ist.
Die Differenz zwischen Netto-Strahlung und
Wärmespeicherung (Rn-G, auch als verfügbare
Strahlungsenergie bezeichnet) steht nun für den latenten und den
fühlbaren Wärmestrom zur Verfügung. Doch wie teilt sich
diese Energie auf?
Stellen Sie die Energiehaushaltsgleichung auf und
machen Sie sich so den Ansatz zur Beantwortung dieser Frage klar.
Rn-G, rH=rw, e
und T sind messbare Größen, bzw. können leicht
aus Messungen abgeleitet werden. Schwieriger ist dies für die
Oberflächentemperatur Ts und der
entsprechende Dampfdruck an der Oberfläche Es(Ts).
Auf Penman (1948) geht ein Ansatz zurück, mit dem
die Oberflächentemperatur angenähert werden kann (Gleichung
in Abb. 3 ).
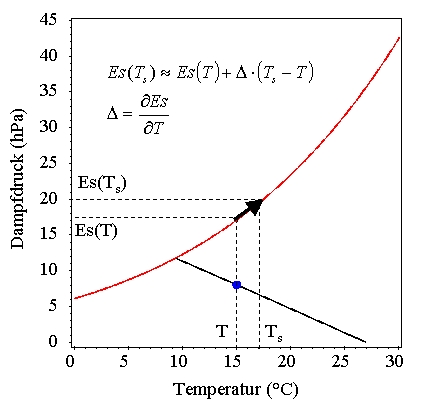
Setzt man diese Näherung für die Oberflächenfeuchte ein und löst die Energiehaushaltsgleichung nach dem latenten Wärmestrom auf, so ergibt sich die sog. Penman-Gleichung als
Mit Gl. 10 können Sie die Verdunstung einer "Freien" Wasseroberfläche, z.B. eines mit Regenwasser bedeckten Waldes bestimmen. Diese Größe wird auch als potenzielle Verdunstung bezeichnet. Die Differenz zwischen Niederschlag und der potenziellen Verdunstung, die sog. atmosphärische Wasserbilanz, wird als ein Indikator für die Wasserversorgung aus allgemeinen Wetterdaten berechnet.
Penman, H.L. (1948): Natural evaporation from open water, bare soil and grass. Proc. Roy. Soc. London A(194), 120-145.
Die aktuelle Verdunstung ist nicht immer gleich der
potenziellen Verdunstung, da Pflanzenbestände die Transpiration
über die Stomata (Schließzellen der Blätter)
regulieren. Monteith (1968) erweiterte Gl. 10 zur modifizierten
Penman-Monteith-Gleichung, indem er den Stomatawiderstand des Bestandes
in die Gleichung integrierte. Dieser Ansatz ist der klassische Fall
eines "big leaf"-Modells: der Bestand wird wie ein einziges
großes Blatt behandelt.
Der Stomatawiderstand ist eine physiologische Größe, für die es empirische Beziehungen zu physikalischen Umweltvariablen gibt, die zuvor aus mikrometeorologischen und ökophysiologischen Feldmessungen abgeleitet wurden.
Als Beispiel für eine Parametrisierung für den rs eines Waldbestandes gibt Wesely et al. (1989) wie folgt an:
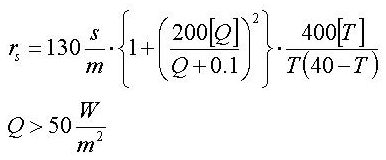 (Gl. 12)
(Gl. 12)Q ist
hier die Globalstrahlung in W/m2 und mit
T die Blatttemperatur in °C. Die beiden Faktoren [Q] und [T] stehen
für die Einheit der Globalstrahlung, bzw. der Blatttemperatur.
Durch die Multiplikation werden diese Terme des empirischen Modells
einheitenlos. Für alle übrigen
Bedingungen (nachts) wird ausschließlich kutikuläre
Verdunstung angenommen (z.B.
rs = 2000 s/m).
Wesely, M.L., Sisteron, D.L. and
Jastrow, J.D., 1989. Parameterisation of surface resistance to gaeous
dry deposition in regional-scale numerical models. Atmospheric
Environment, 23(6): 1293-1304.
Es existieren eine Reihe von anderen
Parametrisierungen, aus denen diese nur aus Gründen der einfachen
Handhabung ausgewählt wurde. Es wird an dieser Stelle
eindrücklich davor gewarnt, diese
Parametrisierung als allgemeingültig anzusehen.
Monteith, J.L.(1965): Evaporation and environment
(Hrsg.): The state and movement of water in living organisms, Symposia
of the Society for Experimental Biology. Cambridge University
Press , 205-234.
Übungen zu dieser Einheit finden sie hier.