

- Wärmetransport und -speicherung-
Temperaturen haben meist eine sehr große Wirkung auf die
physiologischen Prozesse in Organismen und damit auf die biologischen
Stoffumsatzprozesse in Ökosystemen. Ähnliches gilt auch
für rein chemische Reaktionen oder physikalische Prozesse.
Die Temperaturen der in Waldökosystemen im wesentlichen wechselwarmen Organismen und die der unbelebten Ökosystemstrukturen ergeben sich aus den Wärmetransporten zwischen diesen Strukturen und ihrer Umgebung. Ebenso hängen die Temperaturen von der Fähigkeit der Strukturen, Energie aufzunehmen und zu speichern, ab. Diese thermischen Eigenschaften der Strukturen lassen sich direkt auf ihre Materialbeschaffenheit zurückführen.
Als Beispiel soll hier der Wärmetransport, d.h. die Leitung und die Speicherung von Wärme, in Böden behandelt werden.
Der vertikale Wärmestrom, oder besser die Wärmeflussdichte, durch eine Bodenschicht ist proportional zum Vertikalgradienten der Temperatur über dieser Schicht. Die Proportionalitätskonstante k wird als Wärmeleitfähigkeit (thermal conductivity) bezeichnet.Die Wärmeleitfähikeit wird häufig in die allgemeinere Transportgröße, die Wärmediffusivität
(Gl. 1)
κ, umgerechnet (Division von k durchdie Volumenwärme , ρ·c, s.u.) .Wie an Gleichung 2 leicht zu erkennen ist, wird hier nun die Wärmeflussdichte (G in J/(m2 s) := W/m2) proportional zum Vertikalgradienten der Wärmemenge in einem Kubikmeter (in J/m4) gesetzt. (Gl. 2)
Die Wärmediffusivität ist eine reine Transportgröße, d.h. sie enthält, anders als die Wärmeleitfähigkeit, keine Anteile der transportierten Größe mehr und wird in m2/s angegeben. Auf diese Weise lässt sie sich leicht mit anderen Transportkoeffizienten, wie etwa die Diffusivität von Gasen oder der Bewegungsgröße Impuls in Luft vergleichen. Die Wärmediffusivität kann anschaulich, in Analogie zur Elektrik, als ein Transportwiderstand entlang einer Einheitslänge betrachtet werden.
Wie aus der Temperatur, bzw. dem Temperaturgradienten die Wärmemenge, bzw. deren Änderung, berechnet werden kann, sieht man im Zähler der rechten Seite von Gleichung 2. Sie enthält die Volumenwärme, als dem Produkt aus der Dichte ρ und der spezifischen Wärmekapazität c, die beide Materialkonstanten darstellen. Wärmekapazitäten von heterogenen Materialien, ergeben sich aus der Summe der Einzelkapazitäten. Sie finden Werte für Einzelkomponenten und Böden in den Tabellen am Ende dieses Dokumentes (hier). Beachten Sie bitte, dass der Boden ein Drei-Phasensystem ist. Die Dichten etwa der Festsubstanz und des Wassers hängen deshalb sehr stark vom Porenvolumen ab. Bei der Dichteberechnung einer Komponente wird die Masse auf das Gesamtvolumen des Bodens bezogen. Damit sind die Dichten der Bodenkomponenten immer kleiner als die der Reinsubstanzen!
Ändert sich der Wärmeinhalt einer Bodenschicht, so ändert sich auch ihre Temperatur. Die Wärmemenge, die dazu benötigt wird, ergibt sich aus dem Produkt der Wärmekapazität einer Schicht und der Temperaturänderung. Ebenso lässt sich diese Wärmemenge aus der Flussdivergenz, darunter versteht man die Differenz der Wärmeflussdichten an den Rändern der Schicht Go und Gu , ausdrücken. Damit giltDer in der Mitte geklammerte Term ist als negative, infinitesimale Differenz zweier erster Ableitungen per definitionem die zweite Ableitung des Wärmeinhaltes mit der Höhe. Dies wird mit der rechten Seite dieser Differenzialgleichung zum Ausdruck gebracht. . (Gl. 3)
Wenn sich die Dichte und die spezifische Wärmekapazität im Boden nicht ändern, lässt sich aus der obigen Differenzialgleichung für die Wärmeflüsse leicht durch Division beider Seiten durch ρc die Differenzialgleichung für die zeitliche Änderung der Temperatur in einer Schicht
aufschreiben. Die Temperatur wird demnach in einer Schicht größer, wenn die zweite Ableitung positiv ist. Hängt die Temperatur linear von der Tiefe im Boden ab, so ändert sich der Wärmegehalt dieser Schicht nicht mit der Zeit, die zweite Ableitung der Temperatur mit der Tiefe ist Null. Diese Zusammenhänge sind in Abb. 1 illustriert, in der die z-Koordinate nach unten positiv gewertet wird. Dadurch kehrt sich das Vorzeihen gegenüber den obigen Ableitungen um. Im ersten Abschnitt des Profils nimmt die Temperatur konstant mit der Tiefe ab. Danach nimmt die Temperatur weniger stark mit der Tiefe ab. Die Kurve ist nach links gekrümmt, deshalb ist die zweite Ableitung positiv. (Gl. 4)
Abb.1: Ein schematisiertes, vertikales Temperaturprofil in einem homogenen Boden, dessen erste und zweite Ableitungen nach der Tiefe und deren Interpretation hinsichtlich der Wärmeströme (aus Monteith und Unsworth 1990). 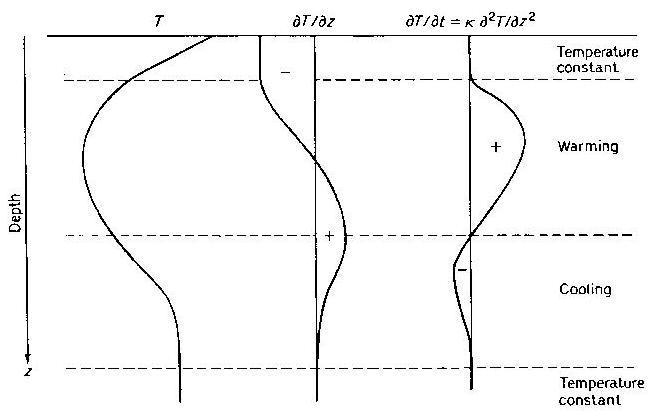
Auf der Basis dieser Differenzialgleichung funktioniert das SAS-Macro waerme in
\\ufobi6\trans\ppoek\ueb5\waermemodell.sas
Benutzen sie dieses Macro, sich über die Bedeutung der thermischen Eigenschaften verschiedener Böden für die Bodentemperaturen im Klaren zu werden. Daten für drei verschiedene Böden mit je drei unterschiedlichen Wassergehalten finden sie ebenfalls hier.
1. Die Wärmeleitfähigkeitsmethode
Ist die Wärmeleitfähigkeit und der vertikale Temperaturgradient der oberen Bodenschicht bekannt, so kann der Wärmestrom durch die Schicht in den Boden mit Gleichung 1 bestimmt werden. Diese Werte liegen in der Regel allerdings nicht vor, so dass diese Methode keine große praktische Bedeutung hat.2. Die Tautochronenmethode
Üblicherweise wird die Wärmeflussdichte in einen Boden mit Hilfe von kontinuierlichen Zeitreihen von in der Regel mehreren Bodentemperatur-Vertikalprofilen bestimmt (Heterogenitätsproblem). Ist die zeitliche Änderung der Temperatur für eine Bodenschicht aus Messungen bekannt, so kann mit Hilfe der Wärmekapazität dieser Schicht der Energiestrom berechnet werden, der die zeitliche Temperaturänderung in dieser Schicht bewirkt hat. Es gilt:
.
Zu beachten ist, dass hier nicht die Volumenwärme, sondern die Wärmekapazität für ein Volumen mit Einheitsfläche und Schichtdicke Verwendung findet. Diese Wärmekapazität hat die Einheit J/(m² K). Die gesamte Wärmeflussdichte durch die Bodenoberfläche, G, ergibt sich in der Summe der Einzelfussdichten über alle Schichten bis hin zu einer Tiefe, in der die zeitlichen Temperaturschwankungen vernachlässigbar klein sind.
Die Übung zu dieser Einheit finden Sie hier.
Table 13.1 in Monteith and
Unsworth (1990): Thermal
properties of soils and their components
(after van Wijk and de Vries.
1963)
| Density | Specific
heat |
Thermal
conductivity |
Thermal
diffusivity |
||
| ρ | c | k | κ | ||
| 103kg | J kg-1 K-1 | W m-1 K-1 | 10-6 m2 s-1 | ||
| Soil components | |||||
| Quartz | 2.66 | 800 | 8.80 | 4.18 | |
| Clay minerals | 2.65 | 900 | 2.92 | 1.22 | |
| Organic matter | 1.30 | 1920 | 0.25 | 0.10 | |
| Water | 1.00 | 4180 | 0.57 | 0.14 | |
| Air(20°C) | 0.0012 | 1010 | 0.025 | 20.50 | |
| Soils |
|||||
| Water content | |||||
| Sandy soil | 0.0 | 1.60 | 800 | 0.30 | 0.24 |
| (40% pore | 0.2 | 1.80 | 1180 | 1.80 | 0.85 |
| space) | 0.4 | 2.00 | 1480 | 2.20 | 0.74 |
| Clay soil | 0.0 | 1.60 | 890 | 0.25 | 0.18 |
| (40% pore | 0.2 | 1.80 | 1250 | 1.18 | 0.53 |
| space) | 0.4 | 2.00 | 1550 | 1.58 | 0.51 |
| Peat soil | 0.0 | 0.30 | 1920 | 0.06 | 0.10 |
| (80% pore | 0.4 | 0.70 | 3300 | 0.29 | 0.13 |
| space) | 0.8 | 1.10 | 3650 | 0.50 | 0.12 |
Tab. -8 (Ibrom 1999): Physikalische Eigenschaften des
Bodens der Fichtenfläche F1.
|
|
cm |
cm |
m |
kJ/(m² K) |
kJ/(m² K) |
|
Mittelpunkt
|
|
|
|||
| Humusauflage |
0;2;5
|
2,8
|
0,06
|
61
|
93
|
| Mineralboden |
5;10
|
7,5
|
0,05
|
91
|
116
|
|
10;20
|
15
|
0,10
|
252
|
330
|
|
|
20;50
|
35
|
0,30
|
523
|
607
|
|
|
50;100
|
75
|
0,50
|
1199
|
1383
|
|
|
100
|
100
|
0,50
|
1234
|
1401
|
|
| Gesamt |
1,51
|
3360
|
3930
|