Lösung zur Übung 1

 

  1. Aufgabe

    2. Berechnen Sie die Temperaturabhängigkeit des Dampfdruckes von 10% bis 100% relativer Luftfeuchte in Schritten à 10% und stellen Sie diese grafisch dar. Wie groß ist die relative Änderung des Sättigungdampfdruckes bei einer Temperaturerhöhung um 10 °C?

  2. Methode

    3. Theorie:

    Der Partialdruck des Wasserdampfes wird als Dampfdruck e bezeichnet. Er wird in hPa angegeben und dient als Angabe des Wasserdampfgehaltes der Luft. Wenn die Luft wasserdampffrei ist, beträgt er 0 hPa. Ist die Luft wasserdampfgesättigt, bezeichnet man den herrschenden Dampfdruck als Sättigungsdampfdruck ES, dabei handelt es sich um den maximal erreichbaren Wert des Dampfdruckes e. Der Sättigungsdampfdruck ist stark von der Lufttemperatur abhängig. Durch die MAGNUS-Formel ( ES = 6.10780*exp[17.08085*TC/(234.175+TC)] ) wird diese Abhängigkeit beschrieben. Vom Luftdruck P ist ES unabhängig.

    Die relative Feuchte RF ist das Verhältnis des aktuellen Dampfdruckes zum Sättigungsdampfdruck. RF ist temperaturabhängig.

    Mit SAS wurde folgender Quellcode entwickelt:

    DATA magnus;

    do Tc=0 to 35 by 1;

    ES = 6.1078 * exp((17.08085*Tc)/(234.175+Tc));/* Sättigungsdampfdruck

    in Pa RF=100%; ES errechnet mit MAGNUS-Formel*/

    e_90=ES*0.9;

    e_80=ES*0.8;

    e_70=ES*0.7;

    e_60=ES*0.6;

    e_50=ES*0.5;

    e_40=ES*0.4;

    e_30=ES*0.3;

    e_20=ES*0.2;

    e_10=ES*0.1;

    output;

    end;

    RUN;

    symbol1 i=join v=none l=1 w=4 c=red;

    symbol2 i=join v=none l=1 w=4 c=blue;

    symbol3 i=join v=none l=1 w=4 c=olive;

    symbol4 i=join v=none l=1 w=4 c=orange;

    symbol5 i=join v=none l=1 w=4 c=yellow;

    symbol6 i=join v=none l=1 w=4 c=pink;

    symbol7 i=join v=none l=1 w=4 c=grey;

    symbol8 i=join v=none l=1 w=4 c=black;

    symbol9 i=join v=none l=1 w=4 c=brown;

    symbol10 i=join v=none l=1 w=4 c=violet;

    axis1 order=0 to 35 by 5 minor=(n=4) label=("Temperatur °C");

    axis2 order=0 to 60 by 10 minor=(n=4) label=( a=90 "Sättigungsdampfdruck hPa");

    PROC GPLOT data=magnus;

    plot (ES e_90 e_80 e_70 e_60 e_50 e_40 e_30 e_20 e_10) *Tc/ overlay

    legend haxis=axis1 vaxis=axis2;

    /* Umlenken der Grafikausgabe in eine gif Datei*/

    goptions device=gif733 gsfmode=replace;

    /* Ausgabename der Datei wird festgesetzt */

    goptions gaccess= "sasgastd>u:\ibrom\ueb1_01_abb1.gif";

    RUN;

    QUIT;

    /* ursprüngliche Ausgabe in des SAS-Grafikkatalog durch: */

    goptions device=win;

     

  3. Ergebnisse
    4.

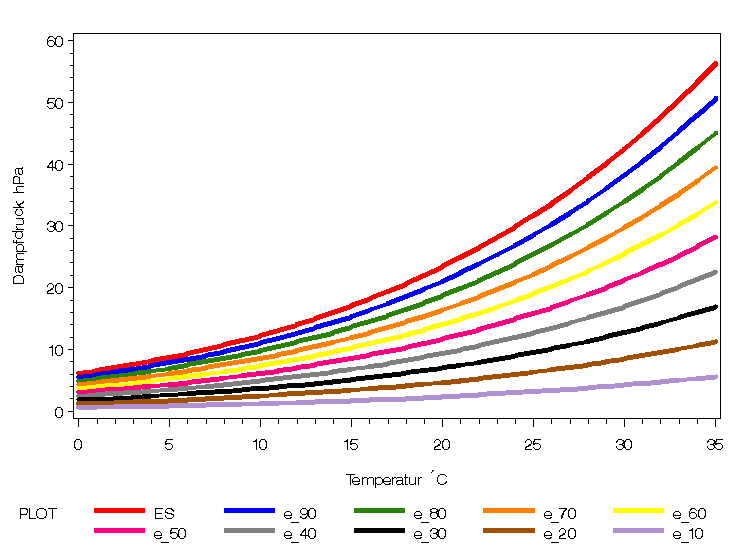
    Abb. 1: Abhängigkeit des Wasserdampfdruckes von der Temperatur und der relativen Feuchte (Kurven von oben bis unten für 100, 90, 80, 70, 60, 50, 40, 30, 20,10%)

     

  4. Diskussion

    5. Die Abhängigkeit zwischen Dampfdruck und Temperatur ist nicht linear (siehe Abb.1). Die Abbildung 1 ist ein Teil des Phasendiagramms des Wassers, wobei die 100%-Linie (oberste Linie) die Gasphase des Wassers nach oben abgrenzt.

    Der Sättigungsdampfdruck steigt mit steigender Temperatur an. Durch eine Erhöhung der Temperatur um 10 °C wird der Sättigungsdampfdruck ungefähr verdoppelt. (Bsp.: 0 °C ES=6.1078 hPa, 10 °C ES=12.2939 hPa, 20 °C ES=23.4200)

    Mit steigender relativer Feuchte nimmt der Sättigungsdampfdruck ebenfalls zu. Diese Informationen ermöglichen es, bei bekannter Temperatur und relativer Feuchte die gesamte Abhängigkeit zu schätzen, wenn man mit dem Startwert 0 °C (ca. 6 hPa) beginnt.

  5. Schlußfolgerungen

Für viele physikalische Abhängigkeiten des Wasserdampfes wird die Sättigungsdampfdruckfunktion benötigt. Dies trifft vor allem bei Vorgängen in der Atmosphäre zu. Um allzu große Fehler zu vermeiden, sollte eine Linearisierung nur in kleinen Temperaturschritten vorgenommen werden.