Übung 2
1.Vergleich der Witterung des Jahres 1996 mit dem langjährigen Mittel.
Fertigen Sie eine Tabelle der Monatsmitteltemperaturen und
-niederschlagssummen der DWD-Station Göttingen für das Jahr 1996
und für den letzten 30-Jahreszeitraum an. Sie finden diese Daten in den monatlichen Witterungsberichten des DWD.
2.Untersuchen Sie die Variabilität der Wetterelemente anhand der
Wetterdaten von zwei Klimastationen über einer Freifläche und im
Buchenwald (vgl. hier). Berechnen Sie den Luftdruck für die Stationen in Göttingen aus den Druck und
Temperaturdaten des Göttinger Waldes. Nutzen Sie zur Berücksichtigung des Höhenunterschiedes bei der Druckangabe
das Skript für das meteorologische Instrumentenpraktikum , Versuch 5, Gleichung 5.3,
den Dampfdruck und das Wasserdampfdrucksättigungsdefizit aus der relativen Feuchte und der Lufttemperatur (vgl. Anleitung
für das meteorologische Instrumentenpraktikum, Versuch 3), Tages- und Monatsmittelwerte für die Lufttemperaturen,
Feuchtegrößen, Luftdruck, Strahlung und Windgeschwindigkeiten, Mittlere monatliche Tagesgänge für diese Größen für einen
Monat (z.B. den Ihrer Teilnehmernummer), Tages-, Monats- und Jahressummen der Niederschlagsmenge.
Stellen Sie die mittleren monatlichen Tagesgänge für Ihren Monat wie folgt dar:
Luft- und Bodentemperaturen von FS und WS PAR- Strahlung FS, WS Wasserdampfdruckdefizit FS, WS
Luftdruck Windgeschwindigkeit FS, WS
3.Besprechen Sie die Ergebnisse hinsichtlich folgender Fragestellungen
Welche Besonderheiten charakterisierten die Witterung des Jahres
1996? Welche Unterschiede haben Sie zwischen Waldinnen- und
Freiflächenklima festgestellt? quantifizieren Sie diese anhand von Mittelwerten und
Schwankungsbreiten Wie lang war die Vegetationsperiode 1996 und wie lange währt sie
im Mittel. Zur Charaktersierung der Vegetationsperiode nehmen Sie
die Tage, ab denen die mittlere Lufttemperatur dauerhaft über 10 °C lagen. Vergleichen Sie Ihre Abschätzung mit dem
Belaubungszeitraum.
Entwickelter Sascode:
libname auf2 "U:\ibrom\auf2";
/*Grafikausgabe*/
filename grafik "U:\ibrom\auf2\grafik\Par.gif";
goptions device=gif hsize=10 cm vsize=10 cm gsfname=grafik gsfmode=replace;
run;quit;
data tmp;
set auf2.bk96;
format saszeit datetime. datum date.;
t = saszeit; /* Datetime. Format Variable sind in Sekunden */
Datum = datepart(saszeit) ; /* ziehe das Datum aus einer Datetime.-Variable */
d = datum; /* Date. Format Variable sind in Tagen */
monat = month(datum);/* der Monat im Jahr als Zahl 1-12 */
m = monat;
jd = Juldate(datum)-96000; /* der julianische Tag 1-365, 366 , ACHTUNG, dies geht bei Jahren > 2000 etwas anders*/
h = hour(saszeit)+minute(saszeit)/60; /* die Stunde einer Datetime.-Variable */
format zeit DDMMYYp8.;
zeit = datepart(saszeit)+ hour(saszeit)/24 + minute(saszeit)/(24*60);
run;
/*proc insight data = tmp;run;*/
/* 1. Sortieren nach Monaten um danach die Mittelwerte berechnen zu können */
proc sort data = tmp; by monat;run;
/* 2. Mitteln der Temperaturen für jeden Monat einzeln */
proc means data = tmp mean noprint;
var TL_fs TL_ws ;
by monat;
output out=TL_mittel mean=;
run;
/*proc insight data=TL_mittel;run;*/
/*Regensummen per Monat*/
proc means data = tmp noprint;
var RI_fs;
by monat;
output out=auf2.regen sum=;
run;
/*proc insight data=jahr1996;run;*/
data Jahr1996;
merge TL_mittel auf2.regen;
run;
/* Herausziehen aller Datensätze für November*/
data auf2.November;
set tmp;
format zeit DDMMYYp8.;
zeit = datepart(saszeit)+ hour(saszeit)/24 + minute(saszeit)/(24*60);
if monat = 11 and year(datum)=1996;
run;
/*proc insight data=auf2.November; run;*/
/*Luftdruckberechnung. Alle benötigten Daten befinden sich in auf2.November*/
data auf2.November;
set auf2.November;
/* TL_FS Temperatur Freiland
TL_WS Temperatur Wald
P_02GW Luftdruck Göttinger Wald
TL_02GW Temperatur Göttinger Wald
P1,P2,P3 = Luftdruck an diesem Ort
z1 = Höhe bez auf P1
z2 = Höhe bez auf P2 */
P3 = P_02GW;
hdiff = 250-450; /*Höhendifferenz der beiden Stationen */
R=287.05; /* Einheit J/kgK Gaskonstante*/
g=-9.81; /* m/s^2 Ergbeschleunigung*/
T1 = ((TL_02GW + TL_FS)/2)+273.15; /*in Kelvin*/
T2 = ((TL_02GW + TL_WS)/2)+273.15;
P1=P3*exp(g*hdiff/(R*T1));
P2=P3*exp(g*hdiff/(R*T2));
/*Sättigungsdampfdruck beider Stationen -> Magnus-Formel*/
DS1 = 6.1078*exp(17.08085*TL_FS/(234.175+TL_FS));
DS2 = 6.1078*exp(17.08085*TL_WS/(234.175+TL_WS));
/*aktueller Dampfdruck, RF in Prozent->Verhältnis*/
D1 = (RF_FS/100) * DS1;
D2 = (RF_WS/100) * DS2;
/*Sättigungsdefizit=Sätt.Dampfdruck-aktuellem Dampfdruck*/
Def1 = DS1-D1;
Def2 = DS2-D2;
run;
/*Darstellung des Luftdruckes beider Stationen*/
proc gplot data=auf2.November;
title1 "Luftdruck in hPa";
symbol1;
symbol2;
/*axis1 order = "11196"d to "311196"d by 1 minor=(n=1) label =("Zeit");*/
axis2 label="Luftdruck[hPa]";
axis1 label ="Zeit";
plot (p1 p2)*zeit / haxis =axis1 vaxis=axis2 overlay;
run;quit;
/*Darstellung des Dampfdruckes für beide Stationen
DS1/Def1/D1*/
proc sort data=auf2.November;
by zeit; run;
proc gplot data=auf2.November;
title1 "Dampfdruck,zugehöriger Sättigungsdampfdruck und entstehendes Defitit [hPa]";
/*aktuell herschender Dampfdruck unter dem Sättigungsdampfdruck*/
axis1 label="Zeit";
axis2 label=(angle=90 "Dampfdruck [hPa]");
legend1 value=(tick=1 "Sättigungsdampfdruck" tick=2 "Defizit" tick=3 "aktueller Dampfdruck");
plot (DS1 Def1 D1)*zeit /haxis =axis1 vaxis=axis2 overlay skipmiss legend=legend1;
plot (DS2 Def2 D2)*zeit /haxis =axis1 vaxis=axis2 overlay skipmiss legend=legend1;
run;Quit;
/*Luft und Bodentemperatur*/
proc gplot data=auf2.November;
title1 "Luft- und Bodentemperatur von FS und WS im November";
symbol1 i=join;
symbol2 i=join;
axis1 label="Zeit";
axis2 label=(angle=90 "Temperatur [°C]");
plot (BT20_WS BT20_FS TL_WS TL_FS)*zeit /haxis =axis1 vaxis=axis2 overlay legend=legend1 skipmiss;
run;Quit;
/*Mittelwerte -> Jahr*/
proc sort data=work.tmp;
by m h;
run;
proc means data=work.tmp noprint;
by m h;
output out=work.mtmp mean=;
run;
proc means data=work.tmp noprint;
by m h;
var RI_FS;
output out=work.stmp sum=;
run;
proc insight data=work.mtmp;
by m;
line Tl_FS Tl_WS * h;
run;
/*Mittelwerte November*/
/* Nach Stunden sortieren*/
proc sort data = auf2.November;
by h;
run;
/*Mittelwerte*/
proc means data = auf2.November noprint;
by h;
output out=MT_11 mean =;
run;
proc insight data = MT_11;
LINE TL_fs TL_ws * H;
run;
/* Darstellung der Temperaturkurve für November */
proc gplot data=MT_11;
title1 "gemittelte Luft(2m Höhe)- und Bodentemperatur(0,2m Tiefe) von FS und WS im November";
legend1;
axis1 order= 0 to 24 by 3 minor=(n=1) label=("Zeit");
axis2 label=(angle=90 "gemittelte Tagesgangtemperatur für Nov [°C]");
plot (TL_fs TL_ws BT20_fs BT20_ws)*H / haxis=axis1 vaxis=axis2 legend=legend1 overlay;
run;quit;
/*PAR-Strahlung keine Einheiten in der Tabelle angegeben*/
proc gplot data=MT_11;
legend1;
title1 "Par-Strahlung : gemittelte Tagesgänge";
axis1 order= 0 to 24 by 3 minor=(n=1) label=("Zeit");
axis2 label=(angle=90 "gemittelte Par-Strahlung für Nov [W/m^2]");
plot (PAR_WS PAR_FS)*H / haxis=axis1 vaxis=axis2 legend=legend1 overlay;
run;quit;
/*Windgeschwindigkeit*/
proc gplot data=MT_11;
title1 "Windgeschwindigkeit, gemittelter Tagesgang für November";
legend1;
axis1 order= 0 to 24 by 3 minor=(n=1) label=("Zeit");
axis2 label=(angle=90 "gemittelte Windgeschwindigkeit für Nov [m/s]");
plot (WG_FS WG_WS)*H / haxis=axis1 vaxis=axis2 legend=legend1 overlay;
run;quit;
data auf2.klima;
input Monat mm temp;
datalines;
1 49 1.0
2 36 1.4
3 49 4.9
4 43 8.1
5 58 12.9
6 74 15.5
7 60 17.4
8 55 17.3
9 52 13.6
10 44 9.2
11 51 4.7
12 58 2.3
;
run;
/*Mittelwert berechnen*/
proc means data=auf2.klima mean noprint;
var mm temp;
output out=auf2.klima1;
run;
proc insight data=auf2.klima1;
run;
/*Kliamdiagramm Göttingen*/
proc gplot data=auf2.klima;
title1 "Klimadaten für Göttingen";
axis1 label="Zeit";
axis2 label=(angle=90 "Temperatur [°C]");
symbol1 i=join;
symbol2 i=join;
plot mm*monat / haxis=axis1 vaxis=axis2 legend=legend1 overlay;
axis3 label=(angle=270 "Niederschlaege [mm]");
plot2 temp*monat / haxis=axis1 vaxis=axis3 legend=legend1 overlay;
run;quit;
/*1996*/
proc gplot data=Jahr1996;
legend1 value=(tick=1 "Temperatur" tick=2 "Niederschlag[mm/Monat]");
legend2
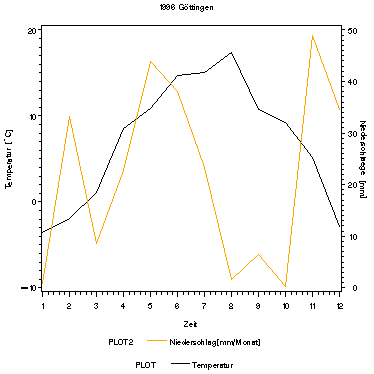
value=(tick=1 "Niederschlag[mm/Monat]");title1 "1996 Göttingen";
axis1 label=("Zeit");
axis2 label=(angle=90 "Temperatur [°C]");
axis3 label=(angle=270 "Niederschlaege [mm]");
plot TL_FS*monat / haxis=axis1 vaxis=axis2 legend=legend1 overlay;
plot2 RI_FS*monat / haxis=axis1 vaxis=axis3 legend=legend2 overlay;
run
;quit;
Ergebnisse :

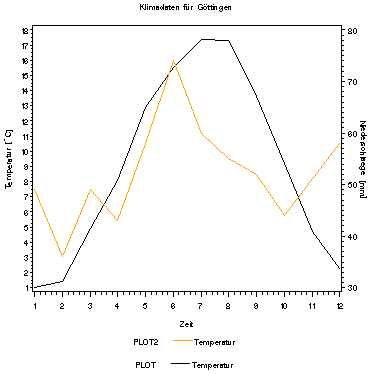
Unterschiede des Jahres 1996 vom langjährigen Mittel :
Im Januar und Dezember werden Durchschnittswerte bis -3°C erreicht was weit unter dem langfristigen Mittel von einem °C liegt. Im Sommer dagegen sind die Temperaturen recht ähnlich. Insgesamt zeichnet sich das einzeln betrachtet Jahr natürlich durch größere Schwankungen aus als die geschwungene Kurve des langfristigen Mittels.
Niederschlag 1996 : 3 Niederschlagsspitzen im Februar,Mai und November. Der mengenmäßig größte Niederschlag fällt im Frühjahr. Von August bis Oktober ist dagegen eine extrem Niederschlagsarme Periode, was im langfristigen Mittel nicht ausgeprägt ist. Dies kann sehr gut zufällig sein, könnte aber vielleicht mit den Daten der letzten 10 Jahre verglichen werden ob sich ein ähnlicher Trend in jüngster Zeit abzeichnet. Die Gesamtniederschlagsmenge ist im langjährigen Mittel größer wobei hier der Schwerpunkt im Sommer liegt. Davon, daß die Klimadaten zuverlässig sind kann ausgegangen werden. Die Jahresdaten zeichnen sich jedoch durch unzuverlässigere Werte aus. Allerdings sind die Missing values für die FS-Fläche bei der Temperatur im erträglichen Rahmen. Beim Niederschlag wirken sich natürlich Meßausfälle auf die Summe aus, doch sind auch sie rel. selten.
Unterschiede einer Freilandfläche (FS) zu einer Waldfläche (WS) im November 1996:
Abb1
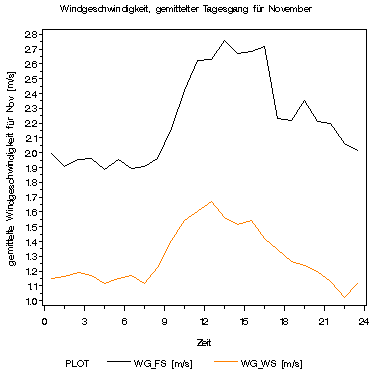
Der relative Verlauf der Kurven ähnelt sich, doch ist natürlich die Windgeschwindigkeit im Freiland wesentlich größer als im Wald, da die Windgeschwindigkeit in 2m Höhe gemessen wurde. Je weiter über Baumhöhe gemessen würde, desto mehr würden sich die Windgeschwindigkeiten wahrscheinlich wieder annähren. Jedoch ist die Reibung über einer Waldfläche größer und damit auch die Kraft die der Windkraft entgegengesetzt ist.
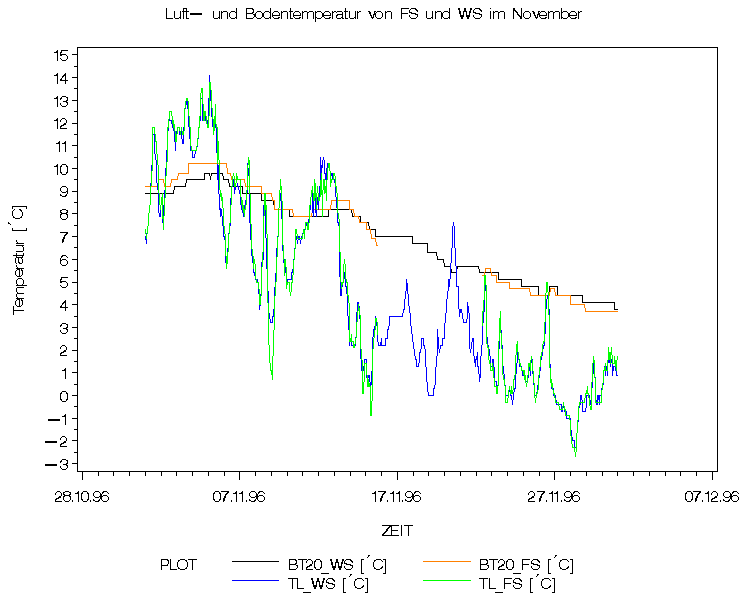
Abb2
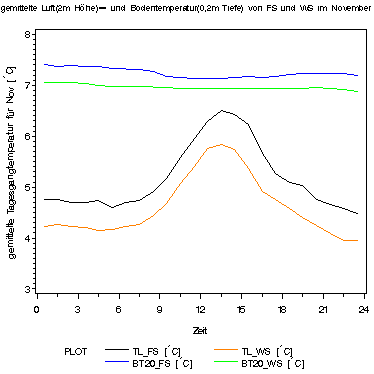
Da beide Stationen die gleiche Höhe haben können die Temperaturwerte direkt verglichen werden. Die Temperaturverläufe sind gleich, nur dass die Temperatur in der Waldfläche um 0.5 °C über den ganzen Tag nach unten verschoben ist, es also durchgängig kühler ist (2m Höhe). Interessant wäre ein Vergleich zu einem Monat in dem noch Belaubung vorhanden war. Erwartet würde, dass die Temperaturamplitude im Wald abnehmen würde und wahrscheinlich die Nachttemperatur über der der Freilandfläche läge.
Die Bodentemperaturen variieren in dieser Tiefe praktisch gar nicht mehr (täglich), zeigen aber, dass auch längerfristig gesehen die Temperatur in der Waldfläche tiefer ist als auf der Freifläche. Jedoch ist die Temperaturdifferenz nur noch 0.3°C. In der nächsten Grafik wird eine mögliche Ursache dafür deutlich :
Abb3

(Die Einheit der y-Achse ist nicht korrekt)
Als Par-Strahlung werden kurzwellige, für die Photosynthese nutzbare Wellenlängen betrachtet. Die Gesamtstrahlung, die die Freilandfäche erhält ist mehr als doppelt so groß. Dadurch wird natürlich die Temperatur direkt beeinflußt. Im November sind die Niederschlagswerte sehr viel größer als zuvor. Durch die vermutete Bewölkung wird deutlich, warum die Par-Strahlung im Oktober (nicht dargestellt) wesentlich höher ist.
Doch was sind die Ursachen für die Flächenunterschiede ? Im November steht die Sonne bereits sehr tief, die
Tageslänge ist kurz. Je tiefer die Sonne steht, desto mehr Baumstämme existieren die den Horizont bedecken.
Desweiteren wäre zu berücksichtigen welche Hangausrichtung beide Stationen haben (Keine Daten).
Abb4
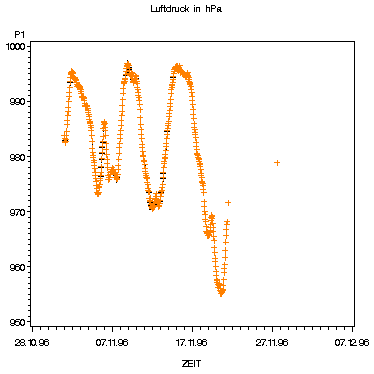
Der Luftdruck wurde nur für eine Station gemessen, die 200 Meter über unseren betrachteten Stationen liegt.
Aus diesem Wert und den bekannten Temperaturen aller Stationen wird nun der Luftdruck abgeschätzt, indem die barometrische Höhenformel benutzt wird. Der Luftdruck in einer Schichtung in der sich die potentielle Temperatur (adiabatisch) nicht ändert ist nur von der Höhe abhängig. In unserem Fall beeinflußt allerdings die Temperatur den Druck. Daher wird aus der jeweiligen Temperatur der oberen und unteren Station ein charakteristischer Mittelwert für diese Luftsäule gebildet und in Kelvin in die Formel eingesetzt.
Die Temperaturunterschiede sind allerdings in unserem Fall zu gering als das ein signifikanter Unterschied zwischen beiden Stationen festgestellt werden könnte.
Gegen Monatsende liegen keine Daten vor. Der Verlauf der Kurve zeigt einen Wechsel zwischen Hochdruck und Tiefdruck. Sinnvoll wäre es noch diese Werte mit dem erwarteten Druck für diese Höhe zu vergleichen oder vielleicht mit einem Niederschlags- oder Windgraphen für diesen Monat.
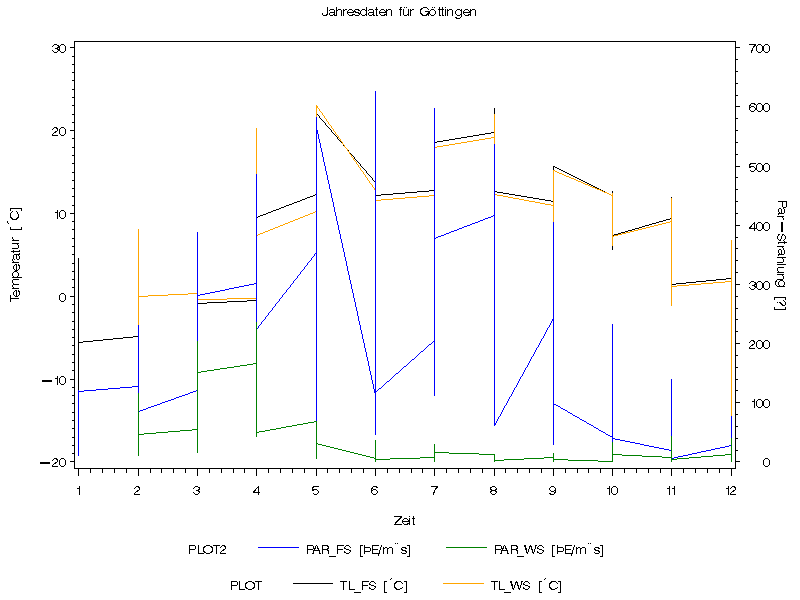
Abb5
Nach den mittleren Tagesgängen sind hier nun die Tagesverläufe des ganzen Monats dargestellt. In der Bodentemperatur wird schön sichtbar, praktisch von Tagesgängen fast bereinigt, daß eine stetige Abkühlung im November stattfindet. Eine Regression der anderen Temperaturwerte dürfte ähnliches liefern (Natürlich etwas versetzt wegen der Trägheit der Bodentemperaturen). Auf dieser Skala werden allerdings die vorher beobachteten Temperaturunterschiede beider Flächen nur noch schwer deutlich, ist der Verlauf doch annährend identisch.
Abb6
Mit "DS1 =
6.1078*exp(17.08085*TL_FS/(234.175+TL_FS))" wird nun der Sättigungsdampfdruck beider Stationen dargestellt. Er ist nur von der Temperatur an der Station abhängig. Mit Hilfe der relativen Feuchtemessung wird nun mit "D1 = (RF_FS/100) * DS1"der aktuelle Dampfdruck bestimmt. Ist die rel. Feuchte 100% sind beide gleich. Mit Def1 = DS1-D1 wird schließlich das jeweilige Sättigungsdefizit bestimmt.
Verlauf : Beide Stationen verhalten sich sehr ähnlich. Da die Temperaturen sehr ähnlich sind, ist auch der Sättigungsdampfdruck fast gleich. Unterschiede im Verlauf des Dampfdruckes müssen also durch die jeweiligen rel. Feuchten beeinflußt sein. Anzunehmen ist wieder, daß ein Monat der Vegetationsperiode ein differenzierteres Verhältnis geliefert hätte mit der Erwartung, daß die rel. Feuchte im Wald größer ist und damit das Defizit geringer. Generell kann im November gesagt werden, daß der aktuelle Dampfdruck auf der Freilandfläche etwas geringer ist,das Wasserdampfdrucksättigungsdefizit damit größer als auf der Waldfläche ist. Erklärung dafür könnte sein, daß die Strahlung auf der Waldfläche geringer ist, damit auch die Temperatur und die rel. Feuchte höher ist. ??
Vegetationsperiode und Belaubungszeitraum :
data
Jahres;set
tmp;run
;
proc
sort data=Jahres; by jd;run;/*proc insight data=Jahres;run;*/
/* 2. Mitteln der Temperaturen für jeden Monat einzeln */
proc
means data = tmp mean noprint;var TL_fs TL_ws ;
by jd;
output out=Tagmittel mean=;
run
;/*proc insight data=Tagmittel;run;*/
data
Tagmittel;set
Tagmittel;if
TL_fs > 10 then x=1;run
;/*proc insight data=Tagmittel;run;*/
proc
print data=Tagmittel;sum
x; /*x=152*/run
;
/*Jahresdaten PAR-Daten->Belaubungszeitraum; Veg -> Temp*/
proc
means data=tmp mean noprint;var
TL_fs TL_ws Par_fs Par_ws;by
jd;output
out=JMittel mean=;run
;
proc
sort data=JMittel;By jd; run;
proc
gplot data=JMittel;title1 "Jahresdaten für Göttingen";
axis1 label=("Zeit");
axis2 label=(angle=90 "Temperatur [°C]");
symbol1 i=join;
symbol2 i=join;
legend1;
plot (TL_fs TL_ws)*jd / haxis=axis1 vaxis=axis2 legend=legend1 overlay;
axis3 label=(angle=270 "Par-Strahlung [?]");
plot2 (Par_fs Par_ws)*jd / haxis=axis1 vaxis=axis3 legend=legend1 overlay;
run
;quit;
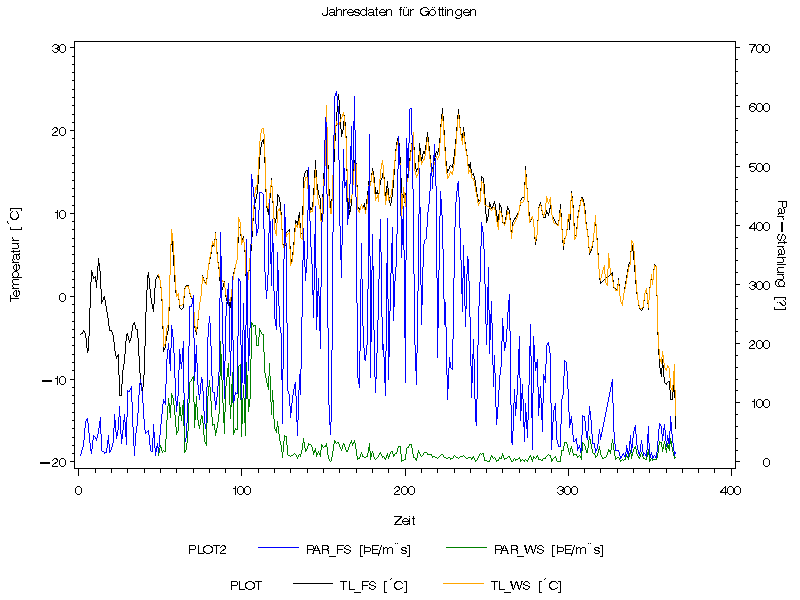
1996 : Die Par-Stahlung nimmt im Wald erst ähnlich zu wie auf der Freifläche. Ab dem Tag 110-120 jedoch wird sie durch den Laubaustrieb auf nahe 0 reduziert Das Ende der Vegetationsperiode ist weniger deutlich (November sehr bewölkt). Vermutlich ab ~Tag 295, da hier ein leichter Anstieg und Annährung an die Freilandfläche auftreten.
Die Vegetationsperiode beginnt bei Tagen deren mittlere Temperatur über 10°C liegt. Insgesamt gibt es 152 Tage an denen das Mittel > 10°C ist. Der erste Anstieg in diesem Diagramm über 10°C findet gleichzeitig mit dem Blattaustrieb ab Tag 110 statt. Danach folgt jedoch noch eine kurze Periode, die unter 10°C liegt, jedoch zum Vegetationszeitraum gerechnet werden sollte. Entscheidend fallen die Temperaturen dann ~ ab Tag 310;
Langjährig ist die Vegetationsperiode als länger anzusetzten, da 1996 ein kühles Jahr war.
(Zur genaueren Untersuchung müßte noch ein präzises Datum bestimmt werden).