Matter Wave Interferometer

 

 

Interferometers with light have been employed for about 150 years and the work with these instruments has brought about tremendous progress in the understanding of physics. Such devices for matter waves can be expected to render similarly great contributions. Since de Broglie's hypothesis of the wave nature of matter, interferometry with atoms has become possible. The wavelength of a de Broglie wave, λ, is determined by the momentum, p, of the particle and is given by the formula

λ = h/p,

where h is Planck's constant.

 

The essential ingredient of any interferometer is a device which allows one to split the beam into spatially separated components without destroying the coherence of the waves. Such beam 'splitters' were found to exist for electrons and also for neutrons in terms of the periodic structures of single crystals. Thus, for about 40 years, interferometry with electrons and neutrons has been successfully performed. For atoms this is a considerably more difficult task and only recently has such a venture been successful (Keith et al., Phys. Rev. Lett. 66, 2693 (1991).

Recently our group developed an interferometer for helium atom beams. The beam splitters are the same nano-structured transmission gratings used in the diffraction experiments . Due to the tremendous progress made in the techniques to fabricate nano-structured devices, such gratings, featuring lattice parameters of less than 100 nm, have recently become available. The periodicity is well suited for diffracting helium atoms in a room temperature beam which have sufficiently large de Broglie wavelengths. Using helium is, in addition, particularly advantageous because of the very weak interaction of these atoms with matter and thus with the grating itself.

The instrument is based on the arrangement of three beam splitters to form an interferometer of the Mach-Zehnder type, well known in classical optics. The setup is sketched in Fig. 1.

 

Fig. 1.

 

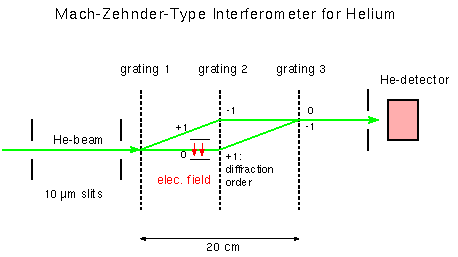
The purpose of first grating is to split the incoming beam into two separate, coherent outgoing beams. Considering the wavelength in our thermal energy helium beam and the lattice parameter of the grid one finds that the angle between the zero order and the first order diffraction beams, Θ =λ/d turns out to be 1 mrad, leading to a spatial separation of the two beams on the second grating of 0.1 mm. Since the beams are merely 0.01 mm wide they are well separated.

Diffraction from the second grating reunites the two beams at the location of the third grating which, again by diffraction, aligns them to propagate as parallel beams to the detector.

If the phase of the de Broglie wave in one of the two beam components is externally changed, for instance by applying an electrical field as indicated in Fig. 1. in terms of the red arrows, the intensity recorded at the detector will change due to partially destructive interference of the two components. A phase shift by λ/2 would lead to complete extinction of the detector signal. Because the wavelength in the helium beam is on the order of 0.1 nm, very small effects will become accessible. As compared to the resolution of interferometers using visible light of wavelengths λ ≈ 500 nm, an atom interferometer would have a factor 5000 improved resolution.

At present we are setting up an experiment to demonstrate the possibility to measure the charge neutrality of a simple atom, in this case, the He atom. The experiment is being carried out in collaboration with the group of Prof. Jacques Vigué (Toulouse, France). Presently there is no completely satisfactory theory to explain why protons and electrons have the same charge to within present day limits of 1 part in more than 1020. Our experiment will be the first to study a simple atom. Although we estimate conservatively a sensitivity of 1 part in 1017 long term measurements and technical improvements should make it possible to significantly increase the sensitivity.

For a collection of more recent publications on atom optics work from the department please click here.
Back

last revision:   E. Hulpke, October 2007