Engineering and Scientific Subroutine Library for AIX Version 3 Release 3: Guide and Reference

SGEMM, DGEMM, CGEMM, and ZGEMM--Combined Matrix Multiplication and Addition for General Matrices, Their Transposes, or Conjugate Transposes

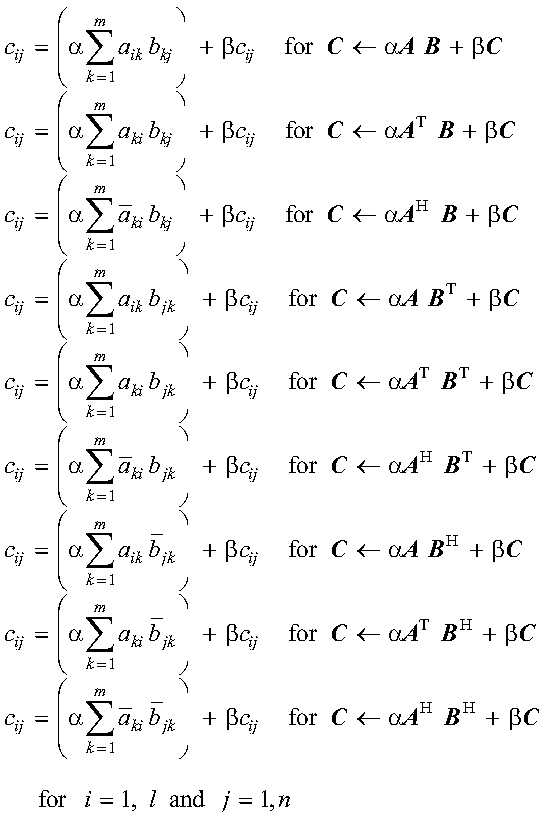
SGEMM and DGEMM can perform any one of the following combined matrix computations, using scalars alpha and beta, matrices A and B or their transposes, and matrix C:

CGEMM and ZGEMM can perform any one of the following combined matrix computations, using scalars alpha and beta, matrices A and B, their transposes or their conjugate transposes, and matrix C:

Table 76. Data Types

Syntax

On Entry

transa

indicates the form of matrix A to use in the computation, where:

If transa = 'N', A is used in the computation.

If transa = 'T', A^T is used in the computation.

If transa = 'C', A^H is used in the computation.

Specified as: a single character; transa = 'N', 'T', or 'C'.

transb

indicates the form of matrix B to use in the computation, where:

If transb = 'N', B is used in the computation.

If transb = 'T', B^T is used in the computation.

If transb = 'C', B^H is used in the computation.

Specified as: a single character; transb = 'N', 'T', or 'C'.

l

is the number of rows in matrix C. Specified as: a fullword integer; 0 <= l <= ldc.

n

is the number of columns in matrix C. Specified as: a fullword integer; n >= 0.

m

has the following meaning, where:

If transa = 'N', it is the number of columns in matrix A.

If transa = 'T' or 'C', it is the number of rows in matrix A.

In addition:

If transb = 'N', it is the number of rows in matrix B.

If transb = 'T' or 'C', it is the number of columns in matrix B.

Specified as: a fullword integer; m >= 0.

alpha

is the scalar alpha. Specified as: a number of the data type indicated in Table 76.

a

is the matrix A, where:

If transa = 'N', A is used in the computation, and A has l rows and m columns.

If transa = 'T', A^T is used in the computation, and A has m rows and l columns.

If transa = 'C', A^H is used in the computation, and A has m rows and l columns.

Note:

No data should be moved to form A^T or A^H; that is, the matrix A should always be stored in its untransposed form.

Specified as: a two-dimensional array, containing numbers of the data type indicated in Table 76, where:

If transa = 'N', its size must be lda by (at least) m.

If transa = 'T' or 'C', its size must be lda by (at least) l.

lda

is the leading dimension of the array specified for a. Specified as: a fullword integer; lda > 0 and:

If transa = 'N', lda >= l.

If transa = 'T' or 'C', lda >= m.

b

is the matrix B, where:

If transb = 'N', B is used in the computation, and B has m rows and n columns.

If transb = 'T', B^T is used in the computation, and B has n rows and m columns.

If transb = 'C', B^H is used in the computation, and B has n rows and m columns.

Note:

No data should be moved to form B^T or B^H; that is, the matrix B should always be stored in its untransposed form.

Specified as: a two-dimensional array, containing numbers of the data type indicated in Table 76, where:

If transb = 'N', its size must be ldb by (at least) n.

If transb = 'T' or 'C', its size must be ldb by (at least) m.

ldb

is the leading dimension of the array specified for b. Specified as: a fullword integer; ldb > 0 and:

If transb = 'N', ldb >= m.

If transb = 'T' or 'C', ldb >= n.

beta

is the scalar beta. Specified as: a number of the data type indicated in Table 76.

c

is the l by n matrix C. Specified as: a two-dimensional array, containing numbers of the data type indicated in Table 76.

ldc

is the leading dimension of the array specified for c. Specified as: a fullword integer; ldc > 0 and ldc >= l.

On Return

c

is the l by n matrix C, containing the results of the computation. Returned as: an ldc by (at least) n array, containing numbers of the data type indicated in Table 76.

Notes

1. All subroutines accept lowercase letters for the transa and transb arguments.
2. For SGEMM and DGEMM, if you specify 'C' for the transa or transb argument, it is interpreted as though you specified 'T'.
3. Matrix C must have no common elements with matrices A or B; otherwise, results are unpredictable. See Concepts.

Function

The combined matrix addition and multiplication is expressed as follows, where a_ik, b_kj, and c_ij are elements of matrices A, B, and C, respectively:

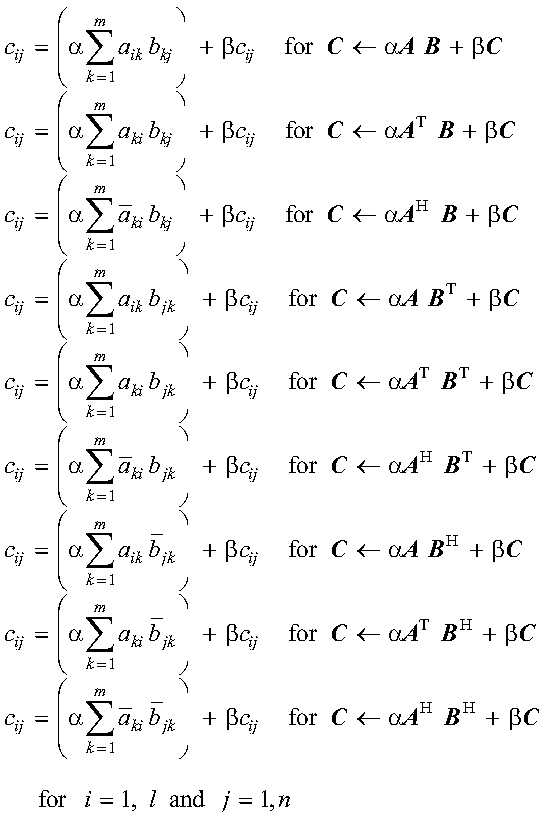
See references [32] and [38]. In the following three cases, no computation is performed:

• l is 0.
• n is 0.
• beta is 1 and alpha is 0.

Assuming the above conditions do not exist, if beta <> 1 and m is 0, then betaC is returned.

Special Usage

Equivalence Rules

The equivalence rules, defined for matrix multiplication of A and B in Special Usage, also apply to the matrix multiplication part of the computation performed by this subroutine. You should use the equivalent rules when you want to transpose or conjugate transpose the multiplication part of the computation. When coding the calling sequences for these cases, be careful to code your matrix arguments and dimension arguments in the order indicated by the rule. Also, be careful that your input and output array C has dimensions large enough to hold the resulting matrix. See Example 4.

Error Conditions

Resource Errors

Unable to allocate internal work area (CGEMM and ZGEMM only).

Computational Errors

None

Input-Argument Errors

1. lda, ldb, ldc <= 0
2. l, m, n < 0
3. l > ldc
4. transa, transb <>  'N', 'T', or 'C'
5. transa = 'N' and l > lda
6. transa = 'T' or 'C' and m > lda
7. transb = 'N' and m > ldb
8. transb = 'T' or 'C' and n > ldb

Example 1

This example shows the computation C<--alphaAB+betaC, where A, B, and C are contained in larger arrays A, B, and C, respectively.

Call Statement and Input

           TRANSA TRANSB  L   N   M  ALPHA  A  LDA  B  LDB  BETA  C  LDC
             |      |     |   |   |    |    |   |   |   |    |    |   |
CALL SGEMM( 'N'  , 'N'  , 6 , 4 , 5 , 1.0 , A , 8 , B , 6 , 2.0 , C , 7 )

        *                              *
        |  1.0   2.0  -1.0  -1.0   4.0 |
        |  2.0   0.0   1.0   1.0  -1.0 |
        |  1.0  -1.0  -1.0   1.0   2.0 |
A    =  | -3.0   2.0   2.0   2.0   0.0 |
        |  4.0   0.0  -2.0   1.0  -1.0 |
        | -1.0  -1.0   1.0  -3.0   2.0 |
        |   .     .     .     .     .  |
        |   .     .     .     .     .  |
        *                              *

        *                        *
        |  1.0  -1.0   0.0   2.0 |
        |  2.0   2.0  -1.0  -2.0 |
B    =  |  1.0   0.0  -1.0   1.0 |
        | -3.0  -1.0   1.0  -1.0 |
        |  4.0   2.0  -1.0   1.0 |
        |   .     .     .     .  |
        *                        *

        *                    *
        | 0.5  0.5  0.5  0.5 |
        | 0.5  0.5  0.5  0.5 |
        | 0.5  0.5  0.5  0.5 |
C    =  | 0.5  0.5  0.5  0.5 |
        | 0.5  0.5  0.5  0.5 |
        | 0.5  0.5  0.5  0.5 |
        |  .    .    .    .  |
        *                    *

Output

        *                        *
        | 24.0  13.0  -5.0   3.0 |
        | -3.0  -4.0   2.0   4.0 |
        |  4.0   1.0   2.0   5.0 |
C    =  | -2.0   6.0  -1.0  -9.0 |
        | -4.0  -6.0   5.0   5.0 |
        | 16.0   7.0  -4.0   7.0 |
        |   .     .     .     .  |
        *                        *

Example 2

This example shows the computation C<--alphaAB^T+betaC, where A and C are contained in larger arrays A and C, respectively, and B is the same size as array B in which it is contained.

Call Statement and Input

           TRANSA TRANSB  L   N   M  ALPHA  A  LDA  B  LDB  BETA  C  LDC
             |      |     |   |   |    |    |   |   |   |    |    |   |
CALL SGEMM( 'N'  , 'T'  , 3 , 3 , 2 , 1.0 , A , 4 , B , 3 , 2.0 , C , 5 )

        *           *
        | 1.0  -3.0 |
A    =  | 2.0   4.0 |
        | 1.0  -1.0 |
        |  .     .  |
        *           *

        *           *
        | 1.0  -3.0 |
B    =  | 2.0   4.0 |
        | 1.0  -1.0 |
        *           *

        *               *
        | 0.5  0.5  0.5 |
        | 0.5  0.5  0.5 |
C    =  | 0.5  0.5  0.5 |
        |  .    .    .  |
        |  .    .    .  |
        *               *

Output

        *                  *
        | 11.0  -9.0   5.0 |
        | -9.0  21.0  -1.0 |
C    =  |  5.0  -1.0   3.0 |
        |   .     .     .  |
        |   .     .     .  |
        *                  *

Example 3

This example shows the computation C<--alphaAB+betaC using complex data, where A, B, and C are contained in larger arrays, A, B, and C, respectively.

Call Statement and Input

           TRANSA TRANSB  L   N   M   ALPHA   A  LDA  B  LDB  BETA   C  LDC
             |      |     |   |   |     |     |   |   |   |    |     |   |
CALL CGEMM( 'N'  , 'N'  , 6 , 2 , 3 , ALPHA , A , 8 , B , 4 , BETA , C , 8 )

ALPHA    =  (1.0, 0.0)
BETA     =  (2.0, 0.0)
 
        *                                    *
        | (1.0, 5.0)  (9.0, 2.0)  (1.0, 9.0) |
        | (2.0, 4.0)  (8.0, 3.0)  (1.0, 8.0) |
        | (3.0, 3.0)  (7.0, 5.0)  (1.0, 7.0) |
A    =  | (4.0, 2.0)  (4.0, 7.0)  (1.0, 5.0) |
        | (5.0, 1.0)  (5.0, 1.0)  (1.0, 6.0) |
        | (6.0, 6.0)  (3.0, 6.0)  (1.0, 4.0) |
        |     .           .           .      |
        |     .           .           .      |
        *                                    *

        *                        *
        | (1.0, 8.0)  (2.0, 7.0) |
B    =  | (4.0, 4.0)  (6.0, 8.0) |
        | (6.0, 2.0)  (4.0, 5.0) |
        |     .           .      |
        *                        *

        *                        *
        | (0.5, 0.0)  (0.5, 0.0) |
        | (0.5, 0.0)  (0.5, 0.0) |
        | (0.5, 0.0)  (0.5, 0.0) |
C    =  | (0.5, 0.0)  (0.5, 0.0) |
        | (0.5, 0.0)  (0.5, 0.0) |
        | (0.5, 0.0)  (0.5, 0.0) |
        |     .           .      |
        |     .           .      |
        *                        *

Output

        *                                *
        | (-22.0, 113.0)  (-35.0, 142.0) |
        | (-19.0, 114.0)  (-35.0, 141.0) |
        | (-20.0, 119.0)  (-43.0, 146.0) |
C    =  | (-27.0, 110.0)  (-58.0, 131.0) |
        |   (8.0, 103.0)    (0.0, 112.0) |
        | (-55.0, 116.0)  (-75.0, 135.0) |
        |       .               .        |
        |       .               .        |
        *                                *

Example 4

This example shows how to obtain the conjugate transpose of AB^H.

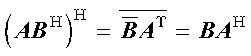
This shows the conjugate transpose of the computation performed in Example 8 for CGEMUL, which uses the following calling sequence:

CALL CGEMUL( A , 4 , 'N' , B , 3 , 'C' , C , 4 , 3 , 2 , 3 )

You instead code the calling sequence for C<--betaC+alphaBA^H, where beta = 0, alpha = 1, and the array C has the correct dimensions to receive the transposed matrix. Because beta is zero, betaC = 0. For a description of all the matrix identities, see Special Usage.

Call Statement and Input

           TRANSA TRANSB  L   N   M   ALPHA   A  LDA  B  LDB  BETA   C  LDC
             |      |     |   |   |     |     |   |   |   |    |     |   |
CALL CGEMM( 'N'  , 'C'  , 3 , 3 , 2 , ALPHA , B , 3 , A , 3 , BETA , C , 4 )

ALPHA    =  (1.0, 0.0)
BETA     =  (0.0, 0.0)
 
        *                         *
        | (1.0, 3.0)  (-3.0, 2.0) |
B    =  | (2.0, 5.0)   (4.0, 6.0) |
        | (1.0, 1.0)  (-1.0, 9.0) |
        *                         *

        *                         *
        | (1.0, 2.0)  (-3.0, 2.0) |
A    =  | (2.0, 6.0)   (4.0, 5.0) |
        | (1.0, 2.0)  (-1.0, 8.0) |
        |     .            .      |
        *                         *

Output

        *                                            *
        | (20.0,   1.0)  (18.0, 23.0)  (26.0,  23.0) |
C    =  | (12.0, -25.0)  (80.0,  2.0)  (56.0, -37.0) |
        | (24.0, -26.0)  (49.0, 37.0)  (76.0,  -2.0) |
        |      .              .             .        |
        *                                            *

Example 5

This example shows the computation C<--alphaA^TB^H+betaC using complex data, where A, B, and C are the same size as the arrays A, B, and C, in which they are contained. Because beta is zero, betaC = 0. (Based on the dimensions of the matrices, A is actually a column vector, and C is actually a row vector.)

Call Statement and Input

           TRANSA TRANSB  L   N   M   ALPHA   A  LDA  B  LDB  BETA   C  LDC
             |      |     |   |   |     |     |   |   |   |    |     |   |
CALL CGEMM( 'T'  , 'C'  , 1 , 3 , 3 , ALPHA , A , 3 , B , 3 , BETA , C , 1 )

ALPHA    =  (1.0, 1.0)
BETA     =  (0.0, 0.0)
 
        *             *
        | (1.0,  2.0) |
A    =  | (2.0,  5.0) |
        | (1.0,  6.0) |
        *             *

        *                                      *
        | (1.0, 6.0)  (-3.0, 4.0)   (2.0, 6.0) |
B    =  | (2.0, 3.0)   (4.0, 6.0)   (0.0, 3.0) |
        | (1.0, 3.0)  (-1.0, 6.0)  (-1.0, 9.0) |
        *                                      *

Output

        *                                         *
C    =  | (86.0, 44.0) (58.0, 70.0) (121.0, 55.0) |
        *                                         *