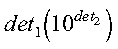
where 1 <= det1 < 10. Returned as: an array of length 2, containing numbers of the data type indicated in Table 92.

These subroutines factor general matrix A using Gaussian
elimination. An estimate of the reciprocal of the condition number and
the determinant of matrix A can also be computed. To solve a
system of equations with one or more right-hand sides, follow the call to
these subroutines with one or more calls to SGES/SGESM or DGES/DGESM,
respectively. To compute the inverse of matrix A, follow the
call to these subroutines with a call to SGEICD and DGEICD,
respectively.
| A, aux, rcond, det | Subroutine |
| Short-precision real | SGEFCD |
| Long-precision real | DGEFCD |
| Fortran | CALL SGEFCD | DGEFCD (a, lda, n, ipvt, iopt, rcond, det, aux, naux) |
| C and C++ | sgefcd | dgefcd (a, lda, n, ipvt, iopt, rcond, det, aux, naux); |
| PL/I | CALL SGEFCD | DGEFCD (a, lda, n, ipvt, iopt, rcond, det, aux, naux); |
If iopt = 0, the matrix is factored.
If iopt = 1, the matrix is factored, and the reciprocal of the condition number is computed.
If iopt = 2, the matrix is factored, and the determinant is computed.
If iopt = 3, the matrix is factored, and the reciprocal of the condition number and the determinant are computed.
Specified as: a fullword integer; iopt = 0, 1, 2, or 3.
If naux = 0 and error 2015 is unrecoverable, aux is ignored.
Otherwise, it is is a storage work area used by this subroutine. Its size is specified by naux.
Specified as: an area of storage, containing numbers of the data type indicated in Table 92.
If naux = 0 and error 2015 is unrecoverable, SGEFCD and DGEFCD dynamically allocate the work area used by the subroutine. The work area is deallocated before control is returned to the calling program.
Otherwise, naux >= n.
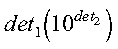
where 1 <= det1 < 10. Returned as: an array of length 2, containing numbers of the data type indicated in Table 92.
Matrix A is factored using Gaussian elimination with partial pivoting (ipvt) to compute the LU factorization of A, where (A=PLU):
On output, the transformed matrix A contains U in the upper triangle and L in the strict lower triangle where ipvt contains the pivots representing permutation P, such that A = PLU.
An estimate of the reciprocal of the condition number, rcond, and the determinant, det, can also be computed by this subroutine. The estimate of the condition number uses an enhanced version of the algorithm described in references [69] and [70].
If n is 0, no computation is performed. See reference [36].
These subroutines call SGEF and DGEF, respectively, to perform the factorization. ipvt is an output vector of SGEF and DGEF. It is returned for use by SGES/SGESM and DGES/DGESM, the solve subroutines.
Error 2015 is unrecoverable, naux = 0, and unable to allocate work area.
Matrix A is singular.
This example shows a factorization of matrix A of order 9. The input is the same as used in SGEF and DGEF. See Example 1. The reciprocal of the condition number and the determinant of matrix A are also computed. The values used to estimate the reciprocal of the condition number in this example are obtained with the following values:
||A||1 = max(6.0, 8.0, 10.0, 12.0, 13.0, 14.0, 15.0, 15.0, 15.0) = 15.0
Estimate of ||A-1||1 = 1091.87
This estimate is equal to the actual rcond of 5.436(10-5), which is computed by SGEICD and DGEICD. (See Example 1.) On output, the value in det, |A|, is equal to 336.
A LDA N IPVT IOPT RCOND DET AUX NAUX
| | | | | | | | |
CALL DGEFCD( A , 9 , 9 , IPVT , 3 , RCOND , DET , AUX , 9 )