Engineering and Scientific Subroutine Library for AIX Version 3 Release 3: Guide and Reference

SGELLS and DGELLS--Linear Least Squares Solution for a General Matrix with Column Pivoting

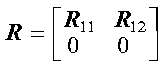
These subroutines compute the minimal norm linear least squares solution of AX is congruent to B, using a QR decomposition with column pivoting.

Table 121. Data Types

Syntax

On Entry

iopt

indicates the type of computation to be performed, where:

If iopt = 0, X is computed.

If iopt = 1, X and the Euclidean Norm of the residual vectors are computed.

Specified as: a fullword integer; iopt = 0 or 1.

a

is the m by n coefficient matrix A. On output, A is overwritten; that is, the original input is not preserved. Specified as: an lda by (at least) n array, containing numbers of the data type indicated in Table 121.

lda

is the leading dimension of the array specified for a. Specified as: a fullword integer; lda > 0 and lda >= m.

b

is the m by nb matrix B, containing the right-hand sides of the linear systems. The nb column vectors of B contain right-hand sides for nb distinct linear least squares problems. On output, B is overwritten; that is, the original input is not preserved.

Specified as: an ldb by (at least) nb array, containing numbers of the data type indicated in Table 121.

ldb

is the leading dimension of the array specified for b. Specified as: a fullword integer; ldb > 0 and ldb >= m.

x

See On Return.

ldx

is the leading dimension of the array specified for x. Specified as: a fullword integer; ldx > 0 and ldx >= n.

rn

See On Return.

tau

is the tolerance tau, used to determine the subset of the columns of A used in the solution. Specified as: a number of the data type indicated in Table 121; tau >= 0. For more information on how to select a value for tau, see Notes.

m

is the number of rows in matrices A and B. Specified as: a fullword integer; m >= 0.

n

is the number of columns in matrix A and the number of rows in matrix X. Specified as: a fullword integer; n >= 0.

nb

is the number of columns in matrices B and X and the number of elements in vector rn. Specified as: a fullword integer; nb > 0.

k

See On Return.

aux

has the following meaning:

If naux = 0 and error 2015 is unrecoverable, aux is ignored.

Otherwise, it is the storage work area used by this subroutine. Its size is specified by naux.

Specified as: an area of storage, containing numbers of the data type indicated in Table 121. On output, the contents of aux are overwritten.

naux

is the size of the work area specified by aux--that is, the number of elements in aux. Specified as: a fullword integer, where:

If naux = 0 and error 2015 is unrecoverable, SGELLS and DGELLS dynamically allocate the work area used by the subroutine. The work area is deallocated before control is returned to the calling program.

Otherwise, It must have the following values:

naux >= 3n+max(n, nb) for SGELLS

naux >= [ceiling(2.5n)+max(n, nb)] for DGELLS

On Return

x

is the solution matrix X, with n rows and nb columns, where:

If k <> 0, the nb column vectors of X contain minimal norm least squares solutions for nb distinct linear least squares problems. The elements in each solution vector correspond to the original columns of A.

If k = 0, the nb column vectors of X are set to 0.

Returned as: an ldx by (at least) nb array, containing numbers of the data type indicated in Table 121.

rn

is the vector rn of length nb, where:

If iopt = 0 or k = 0, rn is not used in the computation.

If iopt = 1, rn_i is the Euclidean Norm of the residual vector for the linear least squares problem defined by the i-th column vector of B.

Returned as: a one-dimensional array of (at least) nb, containing numbers of the data type indicated in Table 121.

k

is the number of columns of matrix A used in the solution. Returned as: a fullword integer; k = (the number of diagonal elements of matrix R exceeding tau in magnitude).

Notes

1. In your C program, argument k must be passed by reference.
2. If ldb >= max(m, n), matrix X and matrix B can be the same; otherwise, matrix X and matrix B can have no common elements, or the results are unpredictable.
3. The following items must have no common elements; otherwise, results are unpredictable:
   • Matrices A and X, vector rn, and the data area specified for aux
   • Matrices A and B, vector rn, and the data area specified for aux.
4. If the relative uncertainty in the matrix B is rho, then:

   tau >= rho||A||_F

   See references [44], [62], and [78] for additional guidance on determining suitable values for tau.

5. When you specify iopt = 0, you must also specify a dummy argument for rn. For more details, see Example 1.
6. You have the option of having the minimum required value for naux dynamically returned to your program. For details, see Using Auxiliary Storage in ESSL.

Function

The minimal norm linear least squares solution of AX is congruent to B is computed using a QR decomposition with column pivoting, where:

A is an m by n real general matrix.

B is an m by nb real general matrix.

X is an n by nb real general matrix.

Optionally, the Euclidean Norms of the residual vectors can be computed. Following are the steps involved in finding the minimal norm linear least squares solution of AX is congruent to B. A is decomposed, using Householder transformations and column pivoting, into the following form:

AP = QR

where:

P is a permutation matrix.

Q is an orthogonal matrix.

R is an upper triangular matrix.

k is the first index, where:

|r_k+1,k+1| <= tau

If k = n, the minimal norm linear least squares solution is obtained by solving RX = Q^TB and reordering X to correspond to the original columns of A.

If k < n, R has the following form:

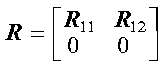
To find the minimal norm linear least squares solution, it is necessary to zero the submatrix R₁₂ using Householder transformations. See references [44], [62], and [78]. If m or n is equal to 0, no computation is performed. These algorithms have a tendency to generate underflows that may hurt overall performance. The system default is to mask underflow, which improves the performance of these subroutines.

Error Conditions

Resource Errors

Error 2015 is unrecoverable, naux = 0, and unable to allocate work area.

Computational Errors

None

Input-Argument Errors

1. iopt <> 0 or 1
2. lda <= 0
3. m > lda
4. ldb <= 0
5. m > ldb
6. ldx <= 0
7. n > ldx
8. m < 0
9. n < 0
10. nb <= 0
11. tau < 0
12. Error 2015 is recoverable or naux<>0, and naux is too small--that is, less than the minimum required value. Return code 1 is returned if error 2015 is recoverable.

Example 1

This example solves the underdetermined system AX is congruent to B. On output, A and B are overwritten. DUMMY is used as a placeholder for argument rn, which is not used in the computation.

Call Statement and Input

            IOPT  A  LDA  B  LDB  X  LDX   RN     TAU   M   N   NB  K   AUX  NAUX
             |    |   |   |   |   |   |     |      |    |   |   |   |    |    |
CALL DGELLS( 0  , A , 2 , B , 2 , X , 3 , DUMMY , TAU , 2 , 3 , 1 , K , AUX , 11 )

        *               *
A    =  | 1.0  2.0  2.0 |
        | 2.0  4.0  5.0 |
        *               *
 
        *     *
B    =  | 1.0 |
        | 4.0 |
        *     *
 
TAU      =   0.0

Output

        *        *
        | -0.600 |
X    =  | -1.200 |
        |  2.000 |
        *        *
 
K        =   2

Example 2

This example solves the overdetermined system AX is congruent to B. On output, A and B are overwritten. DUMMY is used as a placeholder for argument rn, which is not used in the computation.

Call Statement and Input

            IOPT  A  LDA  B  LDB  X  LDX   RN     TAU   M   N   NB  K   AUX  NAUX
             |    |   |   |   |   |   |     |      |    |   |   |   |    |    |
CALL DGELLS( 0  , A , 3 , B , 3 , X , 2 , DUMMY , TAU , 3 , 2 , 2 , K , AUX , 7  )

        *          *
        | 1.0  4.0 |
A    =  | 2.0  5.0 |
        | 3.0  6.0 |
        *          *

        *           *
        | 7.0  10.0 |
B    =  | 8.0  11.0 |
        | 9.0  12.0 |
        *           *
 
TAU      =   0.0

Output

        *                *
X    =  | -1.000  -2.000 |
        |  2.000   3.000 |
        *                *
 
K        =   2

Example 3

This example solves the overdetermined system AX is congruent to B and computes the Euclidean Norms of the residual vectors. On output, A and B are overwritten.

Call Statement and Input

            IOPT  A  LDA  B  LDB  X  LDX  RN   TAU   M   N   NB  K   AUX  NAUX
             |    |   |   |   |   |   |   |     |    |   |   |   |    |    |
CALL DGELLS( 1  , A , 3 , B , 3 , X , 2 , RN , TAU , 3 , 2 , 2 , K , AUX , 7  )

        *           *
        | 1.1  -4.3 |
A    =  | 2.0  -5.0 |
        | 3.0  -6.0 |
        *           *

        *            *
        | -7.0  10.0 |
B    =  | -8.0  11.0 |
        | -9.0  12.0 |
        *            *
 
TAU      =   0.0

Output

        *               *
X    =  | 0.543  -1.360 |
        | 1.785  -2.699 |
        *               *

        *       *
RN   =  | 0.196 |
        | 0.275 |
        *       *
 
K        =   2