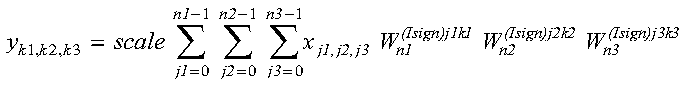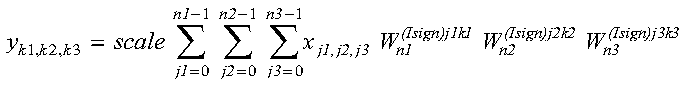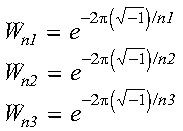Engineering and Scientific Subroutine Library for AIX Version 3 Release 3: Guide and Reference
These subroutines compute the three-dimensional discrete Fourier transform
of complex conjugate even data in a three-dimensional array.
Table 141. Data Types
| X
| Y, scale
| Subroutine
|
| Short-precision complex
| Short-precision real
| SCRFT2
|
| Long-precision complex
| Long-precision real
| DCRFT2
|
- Note:
- For each use, only one invocation of this subroutine is necessary. The
initialization phase, preparing the working storage, is a relatively small
part of the total computation, so it is performed on each invocation.
| Fortran
| CALL SCRFT3 | DCRFT3 (x, inc2x, inc3x,
y, inc2y, inc3y, n1, n2,
n3, isign, scale, aux, naux)
|
| C and C++
| scrft3 | dcrft3 (x, inc2x, inc3x, y,
inc2y, inc3y, n1, n2, n3,
isign, scale, aux, naux);
|
| PL/I
| CALL SCRFT3 | DCRFT3 (x, inc2x, inc3x,
y, inc2y, inc3y, n1, n2,
n3, isign, scale, aux,
naux);
|
- x
- is the array X, containing the three-dimensional data to be
transformed, where each element
xj1,j2,j3, using zero-based
indexing, is stored in
X(j1+j2(inc2x)+j3(inc3x))
for j1 = 0, 1, ..., n1/2,
j2 = 0, 1, ..., n2-1, and
j3 = 0, 1, ..., n3-1. Due to
complex conjugate symmetry, the input consists of only the first
n1/2+1 values along the first dimension of the array, for
j1 = 0, 1, ..., n1/2. The strides for the
elements in the first, second, and third dimensions are assumed to be 1,
inc2x( >= n1/2+1), and
inc3x( >= (n2)(inc2x)),
respectively.
Specified as: an array, containing numbers of the data type indicated
in Table 141. This array must be aligned on a doubleword
boundary. If the array is dimensioned X(LDA1,LDA2,LDA3),
then LDA1 = inc2x,
(LDA1)(LDA2) = inc3x, and
LDA3 >= n3. For information on how to set
up this array, see Setting Up Your Data. For more details, see Notes.
- inc2x
- is the stride between the elements in array X for the second
dimension. Specified as: a fullword integer;
inc2x >= n1/2+1.
- inc3x
- is the stride between the elements in array X for the third
dimension. Specified as: a fullword integer;
inc3x >= (n2)(inc2x).
- y
- See On Return.
- inc2y
- is the stride between the elements in array Y for the second
dimension. Specified as: a fullword integer;
inc2y >= n1+2.
- inc3y
- is the stride between the elements in array Y for the third
dimension. Specified as: a fullword integer;
inc3y >= (n2)(inc2y).
- n1
- is the length of the first dimension of the three-dimensional data in the
array to be transformed. Specified as: a fullword integer;
n1 <= 37748736 and must be one of the values listed in Acceptable Lengths for the Transforms. For all other values specified less than 37748736,
you have the option of having the next larger acceptable value returned in
this argument. For details, see Providing a Correct Transform Length to ESSL.
- n2
- is the length of the second dimension of the three-dimensional data in the
array to be transformed. Specified as: a fullword integer;
n2 <= 37748736 and must be one of the values listed in Acceptable Lengths for the Transforms. For all other values specified less than 37748736,
you have the option of having the next larger acceptable value returned in
this argument. For details, see Providing a Correct Transform Length to ESSL.
- n3
- is the length of the third dimension of the three-dimensional data in the
array to be transformed. Specified as: a fullword integer;
n3 <= 37748736 and must be one of the values listed in Acceptable Lengths for the Transforms. For all other values specified less than 37748736,
you have the option of having the next larger acceptable value returned in
this argument. For details, see Providing a Correct Transform Length to ESSL.
- isign
- controls the direction of the transform, determining the sign
Isign of the exponents of Wn1,
Wn2, and Wn3,
where:
If isign = positive value, Isign = +
(transforming time to frequency).
If isign = negative value,
Isign = - (transforming frequency to time).
Specified as: a fullword integer; isign > 0
or isign < 0.
- scale
- is the scaling constant scale. See Function for its usage. Specified as: a number of the
data type indicated in Table 141, where scale > 0.0 or
scale < 0.0.
- aux
- has the following meaning:
If naux = 0 and error 2015 is unrecoverable, aux
is ignored.
Otherwise, it is a storage work area used by this subroutine.
Specified as: an area of storage, containing naux
long-precision real numbers. On output, the contents are
overwritten.
- naux
- is the number of doublewords in the working storage specified in
aux. Specified as: a fullword integer, where:
If naux = 0 and error 2015 is unrecoverable, SCRFT3 and
DCRFT3 dynamically allocate the work area used by the subroutine. The
work area is deallocated before control is returned to the calling
program.
Otherwise, naux >= (minimum value required for
successful processing). To determine a sufficient value, use the
processor-independent formulas. For all other values specified less
than the minimum value, you have the option of having the minimum value
returned in this argument. For details, see Using Auxiliary Storage in ESSL.
- y
- is the array Y, containing the elements resulting from the
three-dimensional discrete Fourier transform of the data in
X. Each element
yk1,k2,k3, using zero-based
indexing, is stored in
Y(k1+k2(inc2y)+k3(inc3y))
for k1 = 0, 1, ..., n1-1,
k2 = 0, 1, ..., n2-1, and
k3 = 0, 1, ..., n3-1. The strides
for the elements in the first, second, and third dimensions are assumed to be
1, inc2y( >= n1+2), and
inc3y( >= (n2)(inc2y)),
respectively.
Returned as: an array, containing numbers of the data type indicated
in Table 141. If the array is dimensioned
Y(LDA1,LDA2,LDA3), then LDA1 = inc2y,
(LDA1)(LDA2) = inc3y, and
LDA3 >= n3. For information on how to set
up this array, see Setting Up Your Data. For more details, see Notes.
- If you specify the same array for X and Y, then
inc2y must equal (2)(inc2x) and inc3y must equal
(2)(inc3x). In this case, output overwrites input. If
you specify different arrays X and Y, they must have no
common elements; otherwise, results are unpredictable. See Concepts.
- To achieve the best performance, you should align array Y on a
doubleword boundary, and inc2y and inc3y should be even
numbers. In addition, you should use STRIDE--Determine the Stride Value for Optimal Performance in Specified Fourier Transform Subroutines to determine the optimal values for the strides
inc2y and inc3y for your output array. To obtain the
best performance, you should use inc2x = inc2y/2 and
inc3x = inc3y/2. Example 9 in the STRIDE
subroutine description explains how it is used for these subroutines.
For additional information on how to set up your data, see Setting Up Your Data.
Use the following formulas for calculating naux:
- If max(n2, n3) < 252 and:
- If n1 <= 16384, use
naux = 65000.
- If n1 > 16384, use
naux = 60000+1.39n1.
- If n2 >= 252, n3 < 252, and:
- If n1 <= 16384, use
naux = 65000+lambda.
- If n1 > 16384, use
naux = 60000+1.39n1+lambda,
- where lambda = (n2+256)(s+2.28)
- and s = min(64, 1+n1/2).
- If n2 < 252, n3 >= 252, and:
- If n1 <= 16384, use
naux = 65000+psi.
- If n1 > 16384, use
naux = 60000+1.39n1+psi,
- where psi = (n3+256)(s+2.28)
- and s = min(64, (n2)(1+n1/2)).
- If n2 >= 252 and n3 >= 252, use the
larger of the values calculated for cases 2 and 3 above.
If inc2y or inc3y is an odd number, or if array
Y is not aligned on a doubleword boundary, you should add the
following amount to all the formulas given above:
- (1+n1/2)(max(n2, n3))
Use the following formulas for calculating naux:
- If max(n2, n3) < 252 and:
- If n1 <= 4096, use
naux = 62000.
- If n1 > 4096, use
naux = 60000+2.78n1.
- If n2 >= 252, n3 < 252, and:
- If n1 <= 4096, use
naux = 62000+lambda.
- If n1 > 4096, use
naux = 60000+2.78n1+lambda,
- where lambda = ((2)n2+256)(s+4.56)
- and s = min(64, n1/2).
- If n2 < 252, n3 >= 252, and:
- If n1 <= 4096, use
naux = 62000+psi.
- If n1 > 4096, use
naux = 60000+2.78n1+psi,
- where psi = ((2)n3+256)(s+4.56)
- and s = min(64, n2(1+n1/2)).
- If n2 >= 252 and n3 >= 252, use the
larger of the values calculated for cases 2 and 3 above.
The three-dimensional discrete Fourier transform of complex conjugate even
data in array X, with results going into array Y, is
expressed as follows:
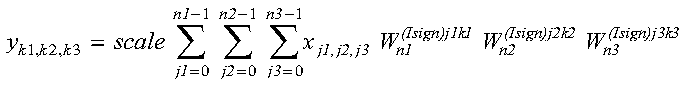
for:
- k1 = 0, 1, ..., n1-1
- k2 = 0, 1, ..., n2-1
- k3 = 0, 1, ..., n3-1
where:
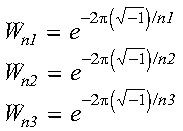
and where:
- xj1,j2,j3 are elements of
array X.
- yk1,k2,k3 are elements of
array Y.
- Isign is + or - (determined by argument
isign).
- scale is a scalar value.
Because of the complex conjugate symmetry, the output in array Y
is real. For scale = 1.0 and isign
being positive, you obtain the discrete Fourier transform, a function of
frequency. The inverse Fourier transform is obtained with
scale = 1.0/((n1)(n2)(n3))
and isign being negative. See references [1], [4], [5], [19],
and [20].
Error 2015 is unrecoverable, naux = 0, and unable to
allocate work area.
None
- n1 > 37748736
- n2 > 37748736
- n3 > 37748736
- inc2x < n1/2+1
- inc3x < (n2)(inc2x)
- inc2y < n1+2
- inc3y < (n2)(inc2y)
- scale = 0.0
- isign = 0
- The length of one of the transforms in n1, n2, or
n3 is not an allowable value. Return code 1 is returned if
error 2030 is recoverable.
- Error 2015 is recoverable or naux<>0, and naux is
too small--that is, less than the minimum required value. Return
code 1 is returned if error 2015 is recoverable.
This example shows how to compute a three-dimensional transform. In
this example, INC2Y = (2)(INC2X) and
INC3Y = (2)(INC3X), so that the same array can
be used for both input and output. The STRIDE subroutine is called to
select good values for the INC2Y and INC3Y
strides. (As explained below, STRIDE is not called for INC2X
and INC3X.) Using the transform lengths
(N1 = 32, N2 = 64, and
N3 = 40) along with the output data type (short-precision
real: 'S'), STRIDE is called once for each stride
needed. First, it is called for INC2Y:
CALL STRIDE (N2,N1+2,INC2Y,'S',0)
The output value returned for INC2Y is 34. (This value is
equal to N1+2.) Then STRIDE is called again for
INC3Y:
CALL STRIDE (N3,N2*INC2Y,INC3Y,'S',0)
The output value returned for INC3Y is 2176. Because
INC3Y is a multiple of INC2Y--that is,
INC3Y = (N2)(INC2Y)--Y
is declared as a three-dimensional array, Y(34,64,40). (In
general, for larger arrays, these types of values for INC2Y and
INC3Y are not returned by STRIDE, and you are probably not able to
declare Y as a three-dimensional array.)
A good stride value for INC2X is INC2Y/2, and a good
stride value for INC3X is INC3Y/2. Also, to
equivalence the X and Y arrays requires
INC2Y = (2)(INC2X) and
INC3Y = (2)(INC3X). Therefore, the values
INC2X = INC2Y/2 = 17 and
INC3X = INC3Y/2 = 1088 are set, and
X is declared as a three-dimensional array,
X(17,64,40).
The arrays are declared as follows:
COMPLEX*8 X(17,64,40)
REAL*4 Y(34,64,40)
REAL*8 AUX(32000)
Arrays X and Y are made equivalent by the following
statement, making them occupy the same storage:
EQUIVALENCE (X,Y)
X INC2X INC3X Y INC2Y INC3Y N1 N2 N3 ISIGN SCALE AUX NAUX
| | | | | | | | | | | | |
CALL SCRFT3( X , 17 , 1088 , Y , 34 , 2176 , 32 , 64 , 40 , 1 , SCALE , AUX , 32000)
SCALE = 1.0
X has (1.0,0.0) in location X(1,1,1) and (0.0,0.0) in all other locations.
Y has 1.0 in all locations.
[ Top of Page | Previous Page | Next Page | Table of Contents | Index ]