Engineering and Scientific Subroutine Library for AIX Version 3 Release 3: Guide and Reference

SPOLY and DPOLY--Polynomial Evaluation

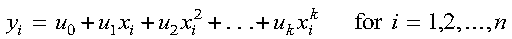
These subroutines evaluate a polynomial of degree k, using coefficient vector u, input vector x, and output vector y:

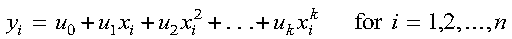
where u_k, x_i, and y_i are elements of u, x, and y, respectively.

Table 143. Data Types

Syntax

On Entry

u

is the coefficient vector u of length k+1. It contains elements u₀, u₁, u₀, u₁, u₂, ..., u_k, which are stored in this order. Specified as: a one-dimensional array of (at least) length 1+k|incu|, containing numbers of the data type indicated in Table 143.

incu

is the stride for vector u. Specified as: a fullword integer. It can have any value.

k

is the degree k of the polynomial. Specified as: a fullword integer; k >= 0.

x

is the input vector x of length n. Specified as: a one-dimensional array of (at least) length 1+(n-1)|incx|, containing numbers of the data type indicated in Table 143.

incx

is the stride for vector x. Specified as: a fullword integer. It can have any value.

y

See On Return.

incy

is the stride for the output vector y. Specified as: a fullword integer. It can have any value.

n

is the number of elements in input vector x and the number of resulting elements in output vector y. Specified as: a fullword integer; n >= 0.

On Return

y

is the output vector y of length n, containing the results of the polynomial evaluation. Returned as: a one-dimensional array of (at least) length 1+(n-1)|incy|, containing numbers of the data type indicated in Table 143.

Note

Vectors u, x, and y must have no common elements; otherwise, results are unpredictable. See Concepts.

Function

The evaluation of the polynomial:

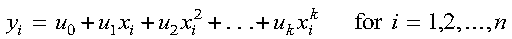
is expressed as follows:

y_i = u₀+x_i (u₁+x_i (u₂+ ...+x_i (u_k-1 + x_iu_k) ...)    for i = 1, 2, ..., n

See reference [81] for Horner's Rule. If n is 0, no computation is performed. For SPOLY, intermediate results are accumulated in long precision.

SPOLY provides the same function as the IBM 3838 function POLY, with restrictions removed. DPOLY provides a long-precision computation that is not included in the IBM 3838 functions. See the IBM 3838 Array Processor Functional Characteristics manual.

Error Conditions

Computational Errors

None

Input-Argument Errors

1. k < 0
2. n < 0

Example 1

This example shows a polynomial evaluation with the degree, K, equal to 0.

Call Statement and Input

            U   INCU   K   X   INCX   Y  INCY  N
            |    |     |   |    |     |   |    |
CALL SPOLY( U , INCU , 0 , X , INCX , Y , 1  , 3 )

Output

Y        =  (4.0, 4.0, 4.0)

Example 2

This example shows a polynomial evaluation, using a negative stride INCU for vector u. For u, processing begins at element U(4) which is 1.0.

Call Statement and Input

            U  INCU  K   X  INCX  Y  INCY  N
            |    |   |   |   |    |   |    |
CALL SPOLY( U , -1 , 3 , X , 1  , Y , 1  , 3 )
 
U        =  (4.0, 3.0, 2.0, 1.0)
X        =  (2.0, 1.0, -3.0)

Output

Y        =  (49.0, 10.0, -86.0)

Example 3

This example shows a polynomial evaluation, using a stride INCX of 0 for input vector x.

Call Statement and Input

            U  INCU  K   X  INCX  Y  INCY  N
            |   |    |   |   |    |   |    |
CALL SPOLY( U , 1  , 3 , X , 0  , Y , 1  , 3 )
 
U        =  (4.0, 3.0, 2.0, 1.0)
X        =  (2.0, . , . )

Output

Y        =  (26.0, 26.0, 26.0)

Example 4

This example shows a polynomial evaluation, using a stride INCX greater than 1 for input vector x, and a negative stride INCY for output vector y. For y, results are stored beginning at element Y(5).

Call Statement and Input

            U  INCU  K   X  INCX  Y  INCY  N
            |   |    |   |   |    |    |   |
CALL SPOLY( U , 1  , 3 , X , 2  , Y , -2 , 3 )
 
U        =  (4.0, 3.0, 2.0, 1.0)
X        =  (2.0, . , -3.0, . , 1.0)

Output

Y        =  (10.0, . , -14.0, . , 26.0)