Engineering and Scientific Subroutine Library for AIX Version 3 Release 3: Guide and Reference

SQINT and DQINT--Quadratic Interpolation

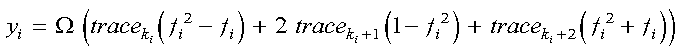
These subroutines perform a quadratic interpolation at specified points in the vector x, using initial linear displacement in the samples s, sample interval g, output scaling parameter OMEGA, and sample reflection times in vector t. The result is returned in vector y.

Table 146. Data Types

Syntax

On Entry

s

is the scalar s, containing the initial linear displacement in samples. Specified as: a number of the data type indicated in Table 146.

g

is the scalar g, containing the sample interval. Specified as: a number of the data type indicated in Table 146; g > 0.0.

omega

is the output scaling parameter OMEGA. Specified as: a number of the data type indicated in Table 146.

x

is the vector x of length n, containing the trace data. Specified as: a one-dimensional array of (at least) length 1+(n-1)|incx|, containing numbers of the data type indicated in Table 146.

incx

is the stride for vector x. Specified as: a fullword integer; incx > 0 or incx < 0.

n

is the number of elements in vector x. Specified as: a fullword integer; n >= 3.

t

is the vector t of length m, containing the sample reflection times to be processed. Specified as: a one-dimensional array of (at least) length 1+(m-1)|inct|, containing numbers of the data type indicated in Table 146.

inct

is the stride for vector t. Specified as: a fullword integer; inct > 0 or inct < 0.

y

See On Return.

incy

is the stride for output vector y. Specified as: a fullword integer; incy > 0 or incy < 0.

m

is the number of elements in vector t and the number of elements in output vector y. Specified as: a fullword integer; m >= 0.

On Return

y

is the vector y of length m, containing the results of the quadratic interpolation. Returned as: a one-dimensional array of (at least) length 1+(m-1)|incy|, containing numbers of the data type indicated in Table 146.

Function

The quadratic interpolation, which is expressed as follows:

for i = 1, 2, ..., m

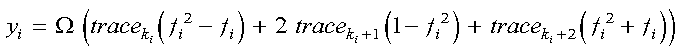
uses the following values:

x is the vector containing the specified points.

s is the initial linear displacement in the samples.

g is a sample interval.

OMEGA is the output scaling parameter.

t is the vector containing the sample reflection times.

and where trace, k, f, and w are four working vectors, and so is a working scalar defined as:

trace₁ = 3x₁-3x₂+x₃

trace_i+1 = x_i    for i = 1, 2, ..., n

so = s+2.0

w_i = so+t_i / g    for i = 1, 2, ..., m

f_i = fraction part of w_i

k_i+1 = integer part of w_i

Note:

Allowing k_i+1 to have a value of 2 results in performance degradation. If possible, avoid specifying a point at which this occurs.

If n or m is 0, no computation is performed.

SQINT provides the same function as the IBM 3838 function INT, with restrictions removed. DQINT provides a long-precision computation that is not included in the IBM 3838 functions. See the IBM 3838 Array Processor Functional Characteristics manual.

Error Conditions

Computational Errors

The condition (k_i+1 > n) or (k_i+1 <= 2) has occurred, where n is the number of elements in vector x. See Function for how to calculate k_i.

• The lower range l and the upper range j of the vector are identified in the computational error message.
• The return code is set to 1.
• The ranges l and j of the vector can be determined at run time by using the ESSL error-handling facilities. To obtain this information, you must use ERRSET to change the number of allowable errors for error code 2100 in the ESSL error option table; otherwise, the default value causes your program to terminate when this error occurs. For details, see What Can You Do about ESSL Computational Errors?.

Input-Argument Errors

1. n < 3
2. m < 0
3. g <= 0
4. incx = 0
5. inct = 0
6. incy = 0

Example 1

This example shows a quadratic interpolation, using vectors with strides of 1.

Call Statement and Input

             S     G   OMEGA  X  INCX  N   T  INCT  Y  INCY  M
             |     |     |    |   |    |   |   |    |   |    |
CALL SQINT( 2.0 , 1.0 , 1.0 , X , 1  , 8 , T , 1  , Y , 1  , 4 )
 
X        =  (1.0, 2.0, 3.0, 4.0, 5.0, 6.0, 7.0, 8.0)
T        =  (1.5, 2.5, 3.5, 4.5)

Output

Y        =  (9.0, 11.0, 13.0, 15.0)

Example 2

This example shows a quadratic interpolation, using vectors with a positive stride of 1 and negative strides of -1.

Call Statement and Input

             S     G   OMEGA  X  INCX  N   T  INCT  Y  INCY  M
             |     |     |    |    |   |   |    |   |   |    |
CALL SQINT( 2.0 , 1.0 , 1.0 , X , -1 , 8 , T , -1 , Y , 1  , 4 )
 
X        =  (1.0, 2.0, 3.0, 4.0, 5.0, 6.0, 7.0, 8.0)
T        =  (1.5, 2.5, 3.5, 4.5)

Output

Y        =  (3.0, 5.0, 7.0, 9.0)

Example 3

This example shows a quadratic interpolation, using vectors with a positive stride greater than 1 and negative strides less than -1.

Call Statement and Input

             S     G   OMEGA  X  INCX  N   T  INCT  Y  INCY  M
             |     |     |    |    |   |   |    |   |   |    |
CALL SQINT( 2.0 , 1.0 , 1.0 , X , -2 , 8 , T , -1 , Y , 2  , 4 )
 
X        =  (1.0, . , 3.0, . , 5.0, . , 7.0, . , 9.0, . , 11.0, . ,
             13.0, . , 15.0)
T        =  (1.36, 2.36, 3.36, 4.36)

Output

Y        =  (4.56, . , 8.56, . , 12.56, . , 16.56)

Example 4

This example shows a quadratic interpolation, using vectors with positive strides and larger values for S and G than shown in the previous examples.

Call Statement and Input

             S      G   OMEGA  X  INCX  N   T  INCT  Y  INCY  M
             |      |     |    |   |    |   |   |    |   |    |
CALL SQINT( 3.0 , 10.0 , 1.0 , X , 1  , 8 , T , 2  , Y , 3  , 4 )
 
X        =  (1.0, 2.0, 3.0, 4.0, 5.0, 6.0, 7.0, 8.0)
T        =  (1.5, . , 2.5, . , 3.5, . , 4.5)

Output

Y        =  (8.3, . , . , 8.5, . , . , 8.7, . , . , 8.9)