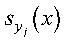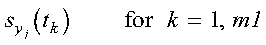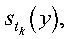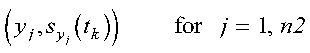Engineering and Scientific Subroutine Library for AIX Version 3 Release 3: Guide and Reference
These subroutines compute the interpolation values at a specified set of
points, using data defined on a rectangular mesh in the x-y plane.
Table 158. Data Types
| x, y, Z, t, u,
aux, S
| Subroutine
|
| Short-precision real
| SCSIN2
|
| Long-precision real
| DCSIN2
|
| Fortran
| CALL SCSIN2 | DCSIN2 (x, y, z, n1,
n2, ldz, t, u, m1, m2,
s, lds, aux, naux)
|
| C and C++
| scsin2 | dcsin2 (x, y, z, n1,
n2, ldz, t, u, m1, m2,
s, lds, aux, naux);
|
| PL/I
| CALL SCSIN2 | DCSIN2 (x, y, z, n1,
n2, ldz, t, u, m1, m2,
s, lds, aux, naux);
|
- x
- is the vector x of length n1, containing the
x-coordinates of the data points that define the spline. The elements
of x must be distinct and sorted into ascending order.
Specified as: a one-dimensional array of (at least) length n1,
containing numbers of the data type indicated in Table 158.
- y
- is the vector y of length n2, containing the
y-coordinates of the data points that define the spline. The elements
of y must be distinct and sorted into ascending order.
Specified as: a one-dimensional array of (at least) length n2,
containing numbers of the data type indicated in Table 158.
- z
- is the matrix Z, containing the data at
(xi, yj) for
i = 1, n1 and j = 1, n2
that defines the spline. Specified as: an ldz by (at
least) n2 array, containing numbers of the data type indicated in Table 158.
- n1
- is the number of elements in vector x and the number of rows in
matrix Z--that is, the number of x-coordinates at which the
spline is defined. Specified as: a fullword integer;
n1 >= 0.
- n2
- is the number of elements in vector y and the number of columns
in matrix Z--that is, the number of y-coordinates at which
the spline is defined. Specified as: a fullword integer;
n2 >= 0.
- ldz
- is the leading dimension of the array specified for z.
Specified as: a fullword integer; ldz > 0 and
ldz >= n1.
- t
- is the vector t of length m1, containing the
x-coordinates at which the spline is evaluated. Specified as: a
one-dimensional array of (at least) length m1, containing numbers of
the data type indicated in Table 158.
- u
- is the vector u of length m2, containing the
y-coordinates at which the spline is evaluated. Specified as: a
one-dimensional array of (at least) length m2, containing numbers of
the data type indicated in Table 158.
- m1
- is the number of elements in vector t--that is, the
number of x-coordinates at which the spline interpolation is evaluated.
Specified as: a fullword integer;
m1 >= 0.
- m2
- is the number of elements in vector u--that is, the
number of y-coordinates at which the spline interpolation is evaluated.
Specified as: a fullword integer;
m2 >= 0.
- s
- See On Return.
- lds
- is the leading dimension of the array specified for s.
Specified as: a fullword integer; lds > 0 and
lds >= m1.
- aux
- has the following meaning:
If naux = 0 and error 2015 is unrecoverable, aux
is ignored.
Otherwise, it is the storage work area used by this subroutine. Its
size is specified by naux.
Specified as: an area of storage, containing numbers of the data type
indicated in Table 156. On output, the contents are overwritten.
- naux
- is the size of the work area specified by aux--that is, the
number of elements in aux. Specified as: a fullword
integer, where:
If naux = 0 and error 2015 is unrecoverable, SCSIN2 and
DCSIN2 dynamically allocate the work area used by the subroutine. The
work area is deallocated before control is returned to the calling
program.
Otherwise, naux >= (10)(max(n1,
n2))+(n2+1)(m1)+2(m2).
- s
- is the matrix S with elements skh
that contain the interpolation values at (tk,
uh) for k = 1, m1 and
h = 1, m2. Returned as: an lds
by (at least) m2 array, containing numbers of the data type indicated
in Table 158.
- The cyclic reduction method used to solve the equations in this subroutine
can generate underflows on well-scaled problems. This does not affect
accuracy, but it may decrease performance. For this reason, you may
want to disable underflow before calling this subroutine.
- Vectors x, y, t, and u, matrix
Z, and the aux work area must have no common elements with
matrix S; otherwise, results are unpredictable.
- The elements within vectors x and y must be
distinct. In addition, the elements in the vectors must be sorted into
ascending order; that is,
x1 < x2 < ...
< xn1 and
y1 < y2 < ...
< yn2. Otherwise, results are
unpredictable. For details on how to do this, see ISORT, SSORT, and DSORT--Sort the Elements of a Sequence.
- You have the option of having the minimum required value for naux
dynamically returned to your program. For details, see Using Auxiliary Storage in ESSL.
Interpolation is performed at a specified set of points:
- (tk, uh)
for k = 1, m1 and h = 1,
m2
by fitting bicubic spline functions with natural boundary conditions, using
the following set of data, defined on a rectangular grid,
(xi, yj) for
i = 1, n1 and j = 1,
n2:
- zij for i = 1,
n1 and j = 1, n2
where tk, uh,
xi, yj, and
zij are elements of vectors t,
u, x, and y and matrix Z,
respectively. In vectors x and y, elements are
assumed to be sorted into ascending order.
The interpolation involves two steps:
- For each j from 1 to n2, the single variable cubic
spline:
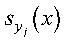
with natural boundary conditions, is constructed using the data
points:
- (xi, zij)
for i = 1, n1
The following interpolation values are then computed:
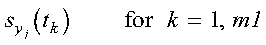
- For each k from 1 to m1, the single variable cubic
spline:
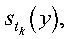
with natural boundary conditions, is constructed using the data
points:
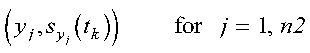
The following interpolation values are then computed:

See references [54] and [60]. Because natural boundary
conditions (zero second derivatives at the end of the ranges) are used for the
splines, unless the underlying function has these properties, interpolated
values near the boundaries may be less satisfactory than elsewhere. If
n1, n2, m1, or m2 is 0, no computation is
performed.
Error 2015 is unrecoverable, naux = 0, and unable to
allocate work area.
None
- n1 < 0 or n1 > ldz
- n2 < 0
- m1 < 0 or m1 > lds
- m2 < 0
- ldz < 0
- lds < 0
- Error 2015 is recoverable or naux<>0, and naux is
too small--that is, less than the minimum required value specified in
the syntax for this argument. Return code 1 is returned if error 2015
is recoverable.
This example computes the interpolated values at a specified set of points,
given by T and U, from a set of data points defined on a
rectangular mesh in the x-y plane, using X, Y, and
Z.
X Y Z N1 N2 LDZ T U M1 M2 S LDS AUX NAUX
| | | | | | | | | | | | | |
CALL SCSIN2( X , Y , Z , 6 , 5 , 6 , T , U , 4 , 3 , S , 4 , AUX , 90 )
X = (0.0, 0.2, 0.3, 0.4, 0.5, 0.7)
Y = (0.0, 0.2, 0.3, 0.4, 0.6)
* *
| 0.000 0.008 0.027 0.064 0.216 |
| 0.008 0.016 0.035 0.072 0.224 |
Z = | 0.027 0.035 0.054 0.091 0.243 |
| 0.064 0.072 0.091 0.128 0.280 |
| 0.125 0.133 0.152 0.189 0.341 |
| 0.343 0.351 0.370 0.407 0.559 |
* *
T = (0.10, 0.15, 0.25, 0.35)
U = (0.05, 0.25, 0.45)
* *
| 0.001 0.017 0.095 |
S = | 0.003 0.019 0.097 |
| 0.016 0.031 0.110 |
| 0.043 0.059 0.137 |
* *
[ Top of Page | Previous Page | Next Page | Table of Contents | Index ]