Engineering and Scientific Subroutine Library for AIX Version 3 Release 3: Guide and Reference

SPTNQ and DPTNQ--Numerical Quadrature Performed on a Set of Points

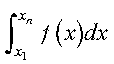
These subroutines approximate the integral of a real valued function specified in tabular form, (x_i, y_i) for i = 1, n. For more than four points, an error estimate is returned along with the resulting value.

Table 160. Data Types

Syntax

On Entry

x

is the vector x of length n, containing the abscissas of the data points to be integrated. The elements of x must be distinct and sorted into ascending or descending order. Specified as: a one-dimensional array of (at least) length n, containing numbers of the data type indicated in Table 160.

y

is the vector y of length n, containing the ordinates of the data points to be integrated. Specified as: a one-dimensional array of (at least) length n, containing numbers of the data type indicated in Table 160.

n

is the number of elements in vectors x and y--that is, the number of data points. The value of n determines the algorithm used by this subroutine. For details, see Function. Specified as: a fullword integer; n >= 2.

xyint

See On Return.

eest

See On Return.

On Return

xyint

is the approximation xyint of the integral. Returned as: a number of the data type indicated in Table 160.

eest

has the following meaning, where:

If n < 5, it is undefined and is set to 0.

If n >= 5, it is an estimate, eest, of the error in the integral, where xyint+eest tends to give a better approximation to the integral than xyint. For details, see references [26] and [61].

Returned as: a number of the data type indicated in Table 160.

Notes

1. In your C program, arguments xyint and eest must be passed by reference.
2. The elements of vector x must be distinct--that is, x_i <> x_j for i <> j,--and they must be sorted into ascending or descending order; otherwise, results are unpredictable. For how to do this, see ISORT, SSORT, and DSORT--Sort the Elements of a Sequence.

Function

The integral is approximated for a real valued function specified in tabular form, (x_i, y_i) for i = 1, n, where x_i are distinct and sorted into ascending or descending order, and n >= 2. If y_i = f(x_i) for i = 1, n, then on output, xyint is an approximation to the integral of the following form:

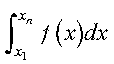
The algorithm used by this subroutine is based on the number of data points used in the computation, where:

• If n = 2, the trapezoid rule is used to do the integration.
• If n = 3, the parabola through the three points is integrated.
• If n >= 4, the method of Gill and Miller is used to do the integration.

For n >= 5, an estimate of the error eest is returned. For the method of Gill and Miller, it is shown that adding the estimate of the error eest to the result xyint often gives a better approximation to the integral than the result xyint by itself. For n < 5, an estimate of the error is not returned. In this case, a value of 0 is returned for eest. See references [61] and [26].

Error Conditions

Computational Errors

None

Input-Argument Errors

n < 2

Example 1

This example shows the result of an integration, where the abscissas in X are sorted into ascending order.

Call Statement and Input

            X   Y   N    XYINT   EEST
            |   |   |      |      |
CALL SPTNQ( X , Y , 10 , XYINT , EEST )
 
X        =  (0.0, 0.4, 1.0, 1.5, 2.1, 2.6, 3.0, 3.4, 3.9, 4.3)
Y        =  (1.0, 2.0, 3.0, 4.0, 5.0, 4.5, 4.0, 3.0, 3.5, 3.3)

Output

XYINT    =  15.137
EEST     =  -0.003

Example 2

This example shows the result of an integration, where the abscissas in X are sorted into descending order.

Call Statement and Input

            X   Y   N    XYINT   EEST
            |   |   |      |      |
CALL SPTNQ( X , Y , 10 , XYINT , EEST )
 
X        =  (4.3, 3.9, 3.4, 3.0, 2.6, 2.1, 1.5, 1.0, 0.4, 0.0)
Y        =  (3.3, 3.5, 3.0, 4.0, 4.5, 5.0, 4.0, 3.0, 2.0, 1.0)

Output

XYINT    =  -15.137
EEST     =  0.003