Engineering and Scientific Subroutine Library for AIX Version 3 Release 3: Guide and Reference

SGLNQ2 and DGLNQ2--Numerical Quadrature Performed on a Function Over a Rectangle Using Two-Dimensional Gauss-Legendre Quadrature

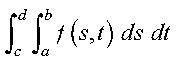
These functions approximate the integral of a real valued function of two variables over a rectangular region, using the Gauss-Legendre Quadrature method of specified order in each variable.

Table 162. Data Types

Syntax

On Entry

subf

is the user-supplied subroutine that evaluates the integrand function. The subroutine should be defined with six arguments: s, n1, t, n2, z, and ldz. For details, see Programming Considerations for the SUBF Subroutine.

Specified as: subf must be declared as an external subroutine in your application program. It can be whatever name you choose.

a

is the lower limit of integration, a, for the first variable integrated. Specified as: a number of the data type indicated in Table 162.

b

is the upper limit of integration, b, for the first variable integrated. Specified as: a number of the data type indicated in Table 162.

n1

is the order of the quadrature method to be used for the first variable integrated. Specified as: a fullword integer; n1 = 1, 2, 3, 4, 5, 6, 8, 10, 12, 14, 16, 20, 24, 32, 40, 48, 64, 96, 128, or 256.

c

is the lower limit of integration, c, for the second variable integrated. Specified as: a number of the data type indicated in Table 162.

d

is the upper limit of integration, d, for the second variable integrated. Specified as: a number of the data type indicated in Table 162.

n2

is the order of the quadrature method to be used for the second variable integrated. Specified as: a fullword integer; n2 = 1, 2, 3, 4, 5, 6, 8, 10, 12, 14, 16, 20, 24, 32, 40, 48, 64, 96, 128, or 256.

z

is the matrix Z, containing the n1 rows and n2 columns of data used to evaluate the integrand function. (The output values from the subf subroutine are placed in Z.) Specified as: an ldz by (at least) n2 array, containing numbers of the data type indicated in Table 162.

ldz

is the size of the leading dimension of the array specified for z. Specified as: a fullword integer; ldz > 0 and ldz >= n1.

On Return

Function value

is the approximation of the integral. Returned as: a number of the data type indicated in Table 162.

Notes

1. Declare the DGLNQ2 function in your program as returning a long-precision real number. Declare the SGLNQ2 function, if necessary, as returning a short-precision real number.
2. The subroutine specified for subf must be declared as external in your program. Also, data types used by subf must agree with the data types specified by this ESSL subroutine. For details on how to set up the subroutine, see Programming Considerations for the SUBF Subroutine.

Function

The integral:

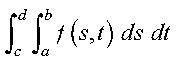
is approximated for a real valued function of two variables s and t, over a rectangular region, using the Gauss-Legendre Quadrature method of specified order in each variable. The region of integration is:

(a, b)    for s

(c, d)    for t

The method gives a good approximation when your integrand is closely approximated by a function of the form f(s, t), where f is a polynomial of degree less than 2(n1) for s and 2(n2) for t. See the function description for SGLNQ and DGLNQ--Numerical Quadrature Performed on a Function Using Gauss-Legendre Quadrature and references [26] and [92]. The result is returned as the function value.

Special Usage

To achieve optimal performance in this subroutine and in the functional evaluation, specify the first variable integrated in this subroutine as the variable having more points. The first variable integrated is the variable in the inner integral. For example, in the following integration, x is the first variable integrated:

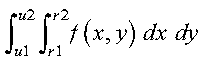
This is the suggested order of integration if the x variable has more points than the y variable. On the other hand, if the y variable has more points, you make y the first variable integrated.

Because the order of integration does not matter to the resulting approximation, you may be able to reverse the order that x and y are integrated and get better performance. This can be expressed as:

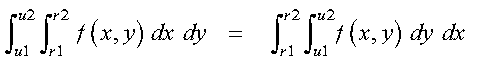
Results are mathematically equivalent. However, because the algorithm is computed in a different way, results may not be bitwise identical.

Table 163 shows how to assign your variables to the _GLNQ2 and subf arguments for the x-y integration shown on the left and for the y-x integration shown on the right. For examples of how to do each of these, see Example 1 and Example 2.

Table 163. How to Assign Your Variables for x-y Integration Versus y-x Integration

Error Conditions

Computational Errors

None

Input-Argument Errors

1. ldz <= 0
2. n1 > ldz
3. n1 or n2 is not an allowable value, as listed in the syntax for this argument.

Example 1

This example shows how to compute the integral of the function f given by:

f(x, y) = e^x sin y

over the intervals (0.0, 2.0) for the first variable x and (-2.0, -1.0) for the second variable y, using the Gauss-Legendre method with 10 points in the x variable and 5 points in the y variable:

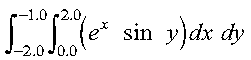
Because the variable x has more points, it is the first variable integrated. This allows the SGLNQ2 subroutine and the FUN1 evaluation to achieve optimal performance. Therefore, the x and y variables correspond to S and T in the FUN1 subroutine. Also, the x and y variables correspond to the A, B, N1 and C, D, N2 sets of arguments, respectively, for SGLNQ2.

Using Fortran for SUBF

The user-supplied subroutine FUN1, which evaluates the integrand function, is coded in Fortran as follows:

   SUBROUTINE FUN1 (S,N1,T,N2,Z,LDZ)
   INTEGER*4 N1,N2,LDZ
   REAL*4 S(*),T(*),Z(LDZ,*)
   DO 1 J=1,N2
   DO 2 I=1,N1
2     Z(I,J)=EXP(S(I))*SIN(T(J))
1     CONTINUE
   RETURN
   END

Note:

The computation for this user-supplied subroutine FUN1 can also be performed by using the following statements in place of the above DO loops, using T1 and T2 as temporary storage areas:

   .
   .
   .
   DO 1 I=1,N1
1     T1(I)=EXP(S(I))
   DO 2 J=1,N2
2     T2(J)=SIN(T(J))
   DO 3 J=1,N2
   DO 4 I=1,N1
4     Z(I,J)=T1(I)*T2(J)
3     CONTINUE
   .
   .
   .

When coding your application, this is the preferred technique. It reduces the number of evaluations performed and, therefore, provides better performance.

Using C for SUBF

The user-supplied subroutine FUN1, which evaluates the integrand function, is coded in C as follows:

   void fun1(s, n1, t, n2, z, ldz)
   float *s, *t, *z;
   int *n1, *n2, *ldz;
   {
        int i, j;
        for(j = 0; j < *n2; ++j, z += *ldz)
            {
             for(i = 0; i < *n1; ++i)
             z[i] = exp(s[i]) * sin(t[j]);
            }
   }

Using C++ for SUBF

The user-supplied subroutine FUN1, which evaluates the integrand function, is coded in C++ as follows:

   void fun1(float *s, int *n1, float *t, int *n2, float *z, int *ldz)
   {
        int i, j;
        for(j = 0; j < *n2; ++j, z += *ldz)
            {
            for(i = 0; i < *n1; ++i)
             z[i] = exp(s[i]) * sin(t[j]);
            }
   }

Using PL/I for SUBF

The user-supplied subroutine FUN1, which evaluates the integrand function, is coded in PL/I as follows:

   FUN1: PROCEDURE(S,N1,T,N2,Z,LDZ) OPTIONS(FORTRAN,NOMAP);
   DCL (N1,N2,LDZ,I,J) REAL FIXED BINARY(31,0);
   DCL (S(10),T(10),Z(5,10)) REAL FLOAT DEC(16) ALIGNED CONNECTED;
   DO J=1 TO N1;
      DO I=1 TO N2;
         Z(I,J)=EXP(S(J))*SIN(T(I));
      END;
   END;
   RETURN;
   END FUN1;

Program Statements and Input

EXTERNAL FUN1
        .
        .
        .
                SUBF    A     B    N1     C      D    N2  Z   LDZ
                 |      |     |    |      |      |    |   |    |
XYINT = SGLNQ2( FUN1 , 0.0 , 2.0 , 10 , -2.0 , -1.0 , 5 , Z , 10 )
        .
        .
        .

Output

XYINT    =  -6.1108

Example 2

This example shows how to reverse the order of integration of the variables x and y. It computes the integral of the function f given by:

f(x, y) = cos x sin y

over the intervals (0.0, 1.0) for the variable x and (0.0, 20.0) for the variable y, using the Gauss-Legendre method with 5 points in the x variable and 48 points in the y variable. Because the order of integration does not matter to the approximation:

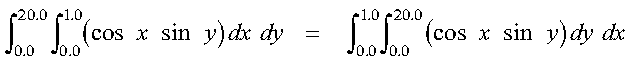
the variable y, having more points, is the first variable integrated (performing the integration shown on the right.) This allows the SGLNQ2 subroutine and the FUN1 evaluation to achieve optimal performance. Therefore, the x and y variables correspond to T and S in the FUN2 subroutine. Also, the x and y variables correspond to the C, D, N2 and A, B, N1 sets of arguments, respectively, for SGLNQ2.

The user-supplied subroutine FUN2, which evaluates the integrand function, is coded in Fortran as follows:

   SUBROUTINE FUN2 (S,N1,T,N2,Z,LDZ)
   INTEGER*4 N1,N2,LDZ
   REAL*4 S(*),T(*),Z(LDZ,*)
   DO 1 J=1,N2
   DO 2 I=1,N1
2     Z(I,J)=COS(T(J))*SIN(S(I))
1     CONTINUE
   RETURN
   END

Note:

The same coding principles for achieving good performance that are noted in Example 1 also apply to this user-supplied subroutine FUN2.

Program Statements and Input

EXTERNAL FUN2.
        .
        .
        .
                SUBF    A      B    N1    C     D    N2   Z  LDZ
                 |      |      |    |     |     |    |    |   |
YXINT = SGLNQ2( FUN2 , 0.0 , 20.0 , 48 , 0.0 , 1.0 , 5  , Z , 48 )
        .
        .
        .

Output

YXINT    =  0.4981