Engineering and Scientific Subroutine Library for AIX Version 3 Release 3: Guide and Reference

SGRAQ and DGRAQ--Numerical Quadrature Performed on a Function Using Gauss-Rational Quadrature

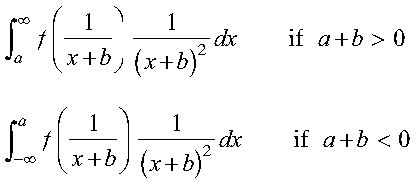
These functions approximate the integral of a real valued function over a semi-infinite interval, using the Gaussian-Rational quadrature method of specified order.

Table 165. Data Types

Syntax

On Entry

subf

is the user-supplied subroutine that evaluates the integrand function. The subroutine should be defined with three arguments: t, y, and n. For details, see Programming Considerations for the SUBF Subroutine.

Specified as: subf must be declared as an external subroutine in your application program. It can be whatever name you choose.

a

has the following meaning, where:

If a+b > 0, it is the lower limit of integration.

If a+b < 0, it is the upper limit of integration.

Specified as: a number of the data type indicated in Table 165.

b

is the centering constant b for the integrand. Specified as: a number of the data type indicated in Table 165.

n

is the order of the quadrature method to be used. Specified as: a fullword integer; n = 1, 2, 3, 4, 5, 6, 8, 10, 12, 14, 16, 20, 24, 32, 40, 48, 64, 96, 128, or 256.

On Return

Function value

 

is the approximation of the integral. Returned as: a number of the data type indicated in Table 165.

Notes

1. Declare the DGRAQ function in your program as returning a long-precision real number. Declare the SGRAQ function, if necessary, as returning a short-precision real number.
2. The subroutine specified for subf must be declared as external in your program. Also, data types used by subf must agree with the data types specified by this ESSL subroutine. The variable x, described under Function, and the argument n correspond to the subf arguments t and n, respectively. For details on how to set up the subroutine, see Programming Considerations for the SUBF Subroutine.

Function

The integral is approximated for a real valued function over a semi-infinite interval, using the Gauss-Rational quadrature method of specified order. The region of integration is:

(a, infinity)    if a+b > 0

(-infinity, a)    if a+b < 0

The method of order n is theoretically exact for integrals of the following form, where f is a polynomial of degree less than 2n:

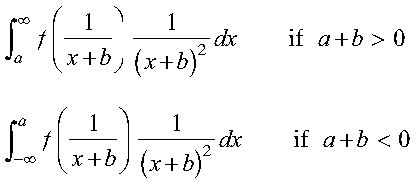
The method of order n is a good approximation when your integrand is closely approximated by a function of the following form, where f is a polynomial of degree less than 2n:

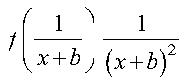
See references [26] and [92]. The result is returned as the function value to a Fortran, C, C++, or PL/I program.

Error Conditions

Computational Errors

None

Input-Argument Errors

1. a+b = 0
2. n is not an allowable value, as listed in the syntax for this argument.

Example 1

This example shows how to compute the integral of the function f given by:

f(x) = (e^1.0/x) / x²

over the interval (-infinity, -2.0), using the Gauss-Rational method with 10 points:

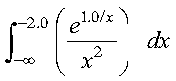
The user-supplied subroutine FUN1, which evaluates the integrand function, is coded in Fortran as follows:

   SUBROUTINE FUN1 (T,Y,N)
   INTEGER*4 N
   REAL*4 T(*),Y(*),TEMP
   DO 1 I=1,N
        TEMP=1.0/T(I)
1       Y(I)=EXP(TEMP)*TEMP**2
   RETURN
   END

Program Statements and Input

EXTERNAL FUN1
        .
        .
        .
              SUBF     A     B    N
               |       |     |    |
XINT = SGRAQ( FUN1 , -2.0 , 0.0 , 10 )
        .
        .
        .

Output

XINT     =  0.393

Example 2

This example shows how to compute the integral of the function f given by:

f(x) = (x-3.0)^-2 + 10(x-3.0)^-11

over the interval (4.0, infinity), using the Gauss-Rational method with 6 points:

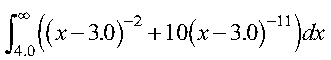
The user-supplied subroutine FUN2, which evaluates the integrand function, is coded in Fortran as follows:

   SUBROUTINE FUN2 (T,Y,N)
   INTEGER*4 N
   REAL*4 T(*),Y(*),TEMP
   DO 1 I=1,N
        TEMP=1.0/(T(I)-3.0)
1       Y(I)=TEMP**2+10.0*TEMP**11
   RETURN
   END

Program Statements and Input

EXTERNAL FUN2
        .
        .
        .
              SUBF    A      B    N
               |      |      |    |
XINT = SGRAQ( FUN2 , 4.0 , -3.0 , 6 )
        .
        .
        .
FUN2     =  (see above)

Output

XINT     =  2.00