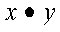

SDOT, DDOT, CDOTU, and ZDOTU compute the dot product of vectors x and y:
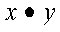
CDOTC and ZDOTC compute the dot product of the complex conjugate of vector x with vector y:
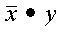
| x, y, Result | Subprogram |
| Short-precision real | SDOT |
| Long-precision real | DDOT |
| Short-precision complex | CDOTU and CDOTC |
| Long-precision complex | ZDOTU and ZDOTC |
| Fortran | SDOT | DDOT | CDOTU | ZDOTU | CDOTC | ZDOTC (n, x, incx, y, incy) |
| C and C++ | sdot | ddot | cdotu | zdotu | cdotc | zdotc (n, x, incx, y, incy); |
| PL/I | SDOT | DDOT | CDOTU | ZDOTU | CDOTC | ZDOTC (n, x, incx, y, incy); |
Declare this function in your program as returning a value of the data type indicated in Table 43.
SDOT, DDOT, CDOTU, and ZDOTU compute the dot product of the vectors x and y, which is expressed as follows:
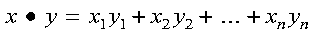
CDOTC and ZDOTC compute the dot product of the complex conjugate of vector x with vector y, which is expressed as follows:
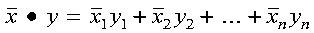
See reference [79]. The result is returned as a function value. If n is 0, then zero is returned as the value of the function.
For SDOT, CDOTU, and CDOTC, intermediate results are accumulated in long precision.
None
n < 0
This example shows how to compute the dot product of two vectors, x and y, having strides of 1.
N X INCX Y INCY
| | | | |
DOTT = SDOT( 5 , X , 1 , Y , 1 )
X = (1.0, 2.0, -3.0, 4.0, 5.0)
Y = (9.0, 8.0, 7.0, -6.0, 5.0)
DOTT = (9.0 + 16.0 - 21.0 - 24.0 + 25.0) = 5.0
This example shows how to compute the dot product of a vector, x, with a stride of 1, and a vector, y, with a stride greater than 1.
N X INCX Y INCY
| | | | |
DOTT = SDOT( 5 , X , 1 , Y , 2 )
X = (1.0, 2.0, -3.0, 4.0, 5.0)
Y = (9.0, . , 7.0, . , 5.0, . , -3.0, . , 1.0)
DOTT = (9.0 + 14.0 - 15.0 - 12.0 + 5.0) = 1.0
This example shows how to compute the dot product of a vector, x, with a negative stride, and a vector, y, with a stride greater than 1. For x, processing begins at element X(5), which is 5.0.
N X INCX Y INCY
| | | | |
DOTT = SDOT( 5 , X , -1 , Y , 2 )
X = (1.0, 2.0, -3.0, 4.0, 5.0)
Y = (9.0, . , 7.0, . , 5.0, . , -3.0, . , 1.0)
DOTT = (45.0 + 28.0 - 15.0 - 6.0 + 1.0) = 53.0
This example shows how to compute the dot product of a vector, x, with a stride of 0, and a vector, y, with a stride of 1. The result in DOTT is x1(y1+...+yn).
N X INCX Y INCY
| | | | |
DOTT = SDOT( 5 , X , 0 , Y , 1 )
X = (1.0, . , . , . , .)
Y = (9.0, 8.0, 7.0, -6.0, 5.0)
DOTT = (1.0) × (9.0 + 8.0 + 7.0 - 6.0 + 5.0) = 23.0
This example shows how to compute the dot product of two vectors, x and y, with strides of 0. The result in DOTT is nx1y1.
N X INCX Y INCY
| | | | |
DOTT = SDOT( 5 , X , 0 , Y , 0 )
X = (1.0, . , . , . , .)
Y = (9.0, . , . , . , .)
DOTT = (5) × (1.0) × (9.0) = 45.0
This example shows how to compute the dot product of two vectors, x and y, containing complex numbers, where x has a stride of 1, and y has a stride greater than 1.
N X INCX Y INCY
| | | | |
DOTT = CDOTU( 3 , X , 1 , Y , 2 )
X = ((1.0, 2.0), (3.0, -4.0), (-5.0, 6.0))
Y = ((10.0, 9.0), . , (-6.0, 5.0), . , (2.0, 1.0))
DOTT = ((10.0 - 18.0 - 10.0) - (18.0 - 20.0 + 6.0),
(9.0 + 15.0 - 5.0) + (20.0 + 24.0 + 12.0))
= (-22.0, 75.0)
This example shows how to compute the dot product of the conjugate of a vector, x, with vector y, both containing complex numbers, where x has a stride of 1, and y has a stride greater than 1.
N X INCX Y INCY
| | | | |
DOTT = CDOTC( 3 , X , 1 , Y , 2 )
X = ((1.0, 2.0), (3.0, -4.0), (-5.0, 6.0))
Y = ((10.0, 9.0), . , (-6.0, 5.0), . , (2.0, 1.0))
DOTT = ((10.0 - 18.0 - 10.0) + (18.0 - 20.0 + 6.0),
(9.0 + 15.0 - 5.0) - (20.0 + 24.0 + 12.0))
= (-14.0, -37.0)