Engineering and Scientific Subroutine Library for AIX Version 3 Release 3: Guide and Reference

SYAX, DYAX, CYAX, ZYAX, CSYAX, and ZDYAX--Multiply a Vector X by a Scalar and Store in a Vector Y

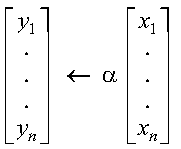
These subprograms perform the following computation, using the scalar alpha and vectors x and y:

y<--alphax

Table 55. Data Types

Syntax

On Entry

n

is the number of elements in vector x and y. Specified as: a fullword integer; n >= 0.

alpha

is the scalar alpha. Specified as: a number of the data type indicated in Table 55.

x

is the vector x of length n. Specified as: a one-dimensional array of (at least) length 1+(n-1)|incx|, containing numbers of the data type indicated in Table 55.

incx

is the stride for vector x. Specified as: a fullword integer. It can have any value.

y

See On Return.

incy

is the stride for vector y. Specified as: a fullword integer. It can have any value.

On Return

y

is the vector y of length n, containing the result of the computation alphax. Returned as: a one-dimensional array of (at least) length 1+(n-1)|incy|, containing numbers of the data type indicated in Table 55.

Notes

1. If you specify the same vector for x and y, then incx and incy must be equal; otherwise, results are unpredictable.
2. If you specify different vectors for x and y, they must have no common elements; otherwise, results are unpredictable. See Concepts.

Function

The computation is expressed as follows:

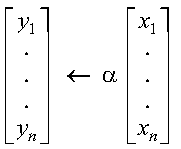
See reference [79]. If n is 0, no computation is performed. For CYAX, intermediate results are accumulated in long precision.

Error Condition

Computational Errors

None

Input-Argument Errors

n < 0

Example 1

This example shows vectors x and y with positive strides.

Call Statement and Input

           N  ALPHA  X  INCX  Y  INCY
           |    |    |   |    |   |
CALL SYAX( 5 , 2.0 , X , 1  , Y , 2  )
 
X        =  (1.0, 2.0, 3.0, 4.0, 5.0)

Output

Y        =  (2.0, . , 4.0, . , 6.0, . , 8.0, . , 10.0)

Example 2

This example shows vectors x and y that have strides of opposite signs. For y, which has negative stride, results are stored beginning in element Y(5).

Call Statement and Input

           N  ALPHA  X  INCX  Y   INCY
           |    |    |   |    |    |
CALL SYAX( 5 , 2.0 , X , 1  , Y , -1  )
 
X        =  (1.0, 2.0, 3.0, 4.0, 5.0)

Output

Y        =  (10.0, 8.0, 6.0, 4.0, 2.0)

Example 3

This example shows a vector, x, with 0 stride. x is treated like a vector of length n, all of whose elements are the same as the single element in x.

Call Statement and Input

           N  ALPHA  X  INCX  Y  INCY
           |    |    |   |    |   |
CALL SYAX( 5 , 2.0 , X , 0  , Y , 1  )
 
X        =  (1.0)

Output

Y        =  (2.0, 2.0, 2.0, 2.0, 2.0)

Example 4

This example shows how SYAX can be used to compute a scalar value. In this case both vectors x and y contain scalar values, and the strides for both vectors are 0. The number of elements to be processed, n, is 1.

Call Statement and Input

           N  ALPHA  X  INCX  Y  INCY
           |    |    |   |    |   |
CALL SYAX( 1 , 2.0 , X , 0  , Y , 0  )
 
X        =  (1.0)

Output

Y        =  (2.0)

Example 5

This example shows a scalar, alpha, and vectors x and y, containing complex numbers, where both vectors have a stride of 1.

Call Statement and Input

           N  ALPHA  X  INCX  Y  INCY
           |    |    |   |    |   |
CALL CYAX( 3 ,ALPHA, X , 1  , Y , 1  )
 
ALPHA    =  (2.0, 3.0)
X        =  ((1.0, 2.0), (2.0, 0.0), (3.0, 5.0))

Output

Y        =  ((-4.0, 7.0), (4.0, 6.0), (-9.0, 19.0))

Example 6

This example shows a scalar, alpha, containing a real number, and vectors x and y, containing complex numbers, where both vectors have a stride of 1.

Call Statement and Input

            N  ALPHA  X  INCX  Y  INCY
            |    |    |   |    |   |
CALL CSYAX( 3 , 2.0 , X , 1  , Y , 1  )
 
X        =  ((1.0, 2.0), (2.0, 0.0), (3.0, 5.0))

Output

Y        =  ((2.0, 4.0), (4.0, 0.0), (6.0, 10.0))