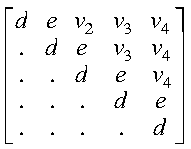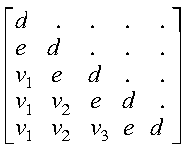Parallel Engineering and Scientific Subroutine Library for AIX Version 2 Release 3: Guide and Reference

PDSYTRD and PZHETRD--Reduce a Real Symmetric or Complex Hermitian Matrix to Tridiagonal Form

PDSYTRD reduces a real symmetric matrix A to symmetric tridiagonal form T by an orthogonal similarity transformation:

T = Q^TAQ

where A represents the global real symmetric submatrix A_{ia:ia+n-1, ja:ja+n-1}.

PZHETRD reduces a complex Hermitian matrix A to symmetric tridiagonal form T by a unitary similarity transformation:

T = Q^HAQ

where A represents the global complex Hermitian submatrix A_{ia:ia+n-1, ja:ja+n-1}

If n = 0, no computation is performed and the subroutine returns after doing some parameter checking.

See references [13] and [21].

Table 104. Data Types

Syntax

On Entry

uplo

indicates whether the upper or lower triangular part of the global submatrix A is referenced, where:

If uplo = 'U', the upper triangular part is referenced.

If uplo = 'L', the lower triangular part is referenced.

Scope: global

Specified as: a single character; uplo = 'U' or 'L'.

n

is the order of submatrix A used in the computation.

Scope: global

Specified as: a fullword integer; n >= 0.

a

is the local part of the global real symmetric or complex Hermitian matrix A. This identifies the first element of the local array A. This subroutine computes the location of the first element of the local subarray used, based on ia, ja, desc_a, p, q, myrow, and mycol; therefore, the leading LOCp(ia+n-1) by LOCq(ja+n-1) part of the local array A must contain the local pieces of the leading ia+n-1 by ja+n-1 part of the global matrix, and:

• If uplo = 'U', the leading n × n upper triangular part of the global submatrix A_{ia:ia+n-1, ja:ja+n-1} must contain the upper triangular part of the submatrix, and the strictly lower triangular part is not referenced.
• If uplo = 'L', the leading n × n lower triangular part of the global submatrix A_{ia:ia+n-1, ja:ja+n-1} must contain the lower triangular part of the submatrix, and the strictly upper triangular part is not referenced.

Scope: local

Specified as: an LLD_A by (at least) LOCq(N_A) array, containing numbers of the data type indicated in Table 104. Details about the square block-cyclic data distribution of global matrix A are stored in desc_a.

ia

is the row index of the global matrix A, identifying the first row of the submatrix A.

Scope: global

Specified as: a fullword integer; 1 <= ia <= M_A and ia+n-1 <= M_A.

ja

is the column index of the global matrix A, identifying the first column of the submatrix A.

Scope: global

Specified as: a fullword integer; 1 <= ja <= N_A and ja+n-1 <= N_A.

desc_a

is the array descriptor for global matrix A, described in the following table:

desc_a	Name	Description	Limits	Scope
1	DTYPE_A	Descriptor type	DTYPE_A=1	Global
2	CTXT_A	BLACS context	Valid value, as returned by BLACS_GRIDINIT or BLACS_GRIDMAP	Global
3	M_A	Number of rows in the global matrix	If n = 0: M_A >= 0 Otherwise: M_A >= 1	Global
4	N_A	Number of columns in the global matrix	If n = 0: N_A >= 0 Otherwise: N_A >= 1	Global
5	MB_A	Row block size	MB_A >= 1	Global
6	NB_A	Column block size	NB_A >= 1	Global
7	RSRC_A	The process row of the p × q grid over which the first row of the global matrix is distributed	0 <= RSRC_A < p	Global
8	CSRC_A	The process column of the p × q grid over which the first column of the global matrix is distributed	0 <= CSRC_A < q	Global
9	LLD_A	The leading dimension of the local array	LLD_A >= max(1,LOCp(M_A))	Local

Specified as: an array of (at least) length 9, containing fullword integers.

d

See On Return.

e

See On Return.

tau

See On Return.

work

has the following meaning:

If lwork = 0, work is ignored.

If lwork <> 0, work is the work area used by this subroutine, where:

• If lwork <> -1, its size is (at least) of length lwork.
• If lwork = -1, its size is (at least) of length 1.

Scope: local

Specified as: an area of storage containing numbers of data type indicated in Table 104.

lwork

is the number of elements in array WORK.

Scope:

• If lwork >= 0, lwork is local
• If lwork = -1, lwork is global

Specified as: a fullword integer; where:

• If lwork = 0, PDSYTRD and PZHETRD dynamically allocate the work area used by the subroutine. The work area is deallocated before control is returned to the calling program. This option is an extension to the ScaLAPACK standard.
• If lwork = -1, PDSYTRD and PZHETRD perform a work area query and return the minimum size of work in work₁. No computation is performed and the subroutine returns after error checking is complete.
• Otherwise, it must have the following value:

  lwork >= max(nb(np+1), 3nb)

  where:

  nb = MB_A = NB_A

  iarow = mod(RSRC_A+(ia-1)/nb, nprow).

  np = NUMROC(n, nb, myrow, iarow, nprow)

info

See On Return.

On Return

a

is the updated local part of the global matrix A, containing the results of the computation, where:

• If uplo = 'U', the diagonal and first superdiagonal of A_{ia:ia+n-1, ja:ja+n-1} are overwritten by the corresponding elements of the tridiagonal matrix T. The elements above the first superdiagonal are overwritten with v_1:i-1. These elements with tau represent the matrix Q as a product of elementary reflectors.
• If uplo = 'L', the diagonal and first subdiagonal of A_{ia:ia+n-1, ja:ja+n-1} are overwritten by the corresponding elements of the tridiagonal matrix T. The elements below the first subdiagonal are overwritten with v_i+2:n. These elements with tau represent the matrix Q as a product of elementary reflectors.

See Function, for more information.

Scope: local

Returned as: an LLD_A by (at least) LOCq(N_A) array, containing numbers of the data type indicated in Table 104. Details about the square block-cyclic data distribution of global matrix A are stored in desc_a.

d

is the updated local part of the global matrix D, where d_ja:ja+n-1 contains the diagonal elements of the tridiagonal matrix T.

This identifies the first element of the local array D. This subroutine computes the location of the first element of the local subarray used, based on ja, desc_a, p, q, myrow, and mycol; therefore, the leading 1 by LOCq(ja+n-1) part of the local array D must contain the local pieces of the leading 1 by ja+n-1 part of the global matrix D.

A copy of the vector d, with a block size of NB_A and global index ja, is returned to each row of the process grid. The process column over which the first column of d is distributed is CSRC_A.

Scope: local

Returned as: a 1 by (at least) LOCq(N_A) array, containing numbers of the data type indicated in Table 104.

e

is the updated local part of the global matrix E, containing the off-diagonal elements of the tridiagonal matrix T, where:

If uplo = 'U', then e_ja = 0 and e_ja+1:ja+n-1 contains the superdiagonal elements of the tridiagonal matrix T.

If uplo = 'L', then e_ja:ja+n-2 contains the subdiagonal elements of the tridiagonal matrix T, and e_ja+n-1 = 0.

This identifies the first element of the local array E. This subroutine computes the location of the first element of the local subarray used, based on ja, desc_a, p, q, myrow, and mycol; therefore, the leading 1 by LOCq(ja+n-1) part of the local array E must contain the local pieces of the leading 1 by ja+n-1 part of the global matrix E.

A copy of the vector e, with a block size of NB_A and global index ja, is returned to each row of the process grid. The process column over which the first column of E is distributed is CSRC_A.

Scope: local

Returned as: a 1 by (at least) LOCq(N_A) array, containing numbers of the data type indicated in Table 104.

tau

is the updated local part of the global matrix tau, containing the scalar factors of the elementary reflectors, where:

If uplo = 'U', then tau_ja is zero and tau_ja+1:ja+n-1 contains the scalar factors of the elementary reflectors.

If uplo = 'L', then tau_ja:ja+n-2 contains the scalar factors of the elementary reflectors and tau_ja+n-1 is zero.

This identifies the first element of the local array tau. This subroutine computes the location of the first element of the local subarray used, based on ja, desc_a, p, q, myrow, and mycol; therefore, the leading 1 by LOCq(ja+n-1) part of the local array tau must contain the local pieces of the leading 1 by ja+n-1 part of the global matrix tau.

A copy of the vector tau, with a block size of NB_A and global index ja, is returned to each row of the process grid. The process column over which the first column of tau is distributed is CSRC_A.

Scope: local

Returned as: a 1 by (at least) LOCq(N_A) array, containing numbers of the data type indicated in Table 104.

work

is the work area used by this subroutine if lwork <> 0, where:

If lwork <> 0 and lwork <> -1, its size is (at least) of length lwork.

If lwork = -1, its size is (at least) of length 1.

Scope: local

Returned as: an area of storage, where:

If lwork >= 1 or lwork = -1, then work₁ is set to the minimum lwork value and contains numbers of the data type indicated in Table 104. Except for work₁, the contents of work are overwritten on return.

info

indicates that a successful computation occurred.

Scope: global

Returned as: a fullword integer; info = 0.

Notes and Coding Rules

1. This subroutine accepts lowercase letters for the uplo argument.
2. In your C program, argument info must be passed by reference.
3. The imaginary parts of the diagonal elements of a complex Hermitian matrix A are assumed to be zero, so you do not have to set these values. On output, they are set to zero, except when n is equal to zero.
4. Matrix A, d, e, tau, and work must have no common elements; otherwise, results are unpredictable.
5. The NUMROC utility subroutine can be used to determine the values of LOCp(M_) and LOCq(N_) used in the argument descriptions above. For details, see Determining the Number of Rows and Columns in Your Local Arrays and NUMROC--Compute the Number of Rows or Columns of a Block-Cyclically Distributed Matrix Contained in a Process.
6. The global real symmetric or complex Hermitian matrix A must be distributed using a square block-cyclic distribution; that is, MB_A = NB_A.
7. The global real symmetric or complex Hermitian matrix A must be aligned on a block boundary; that is:
   • ia-1 must be a multiple of MB_A
   • ja-1 must be a multiple of NB_A
8. There are no array descriptors for d, e, and tau. These are all row distributed vectors with block size NB_A, local arrays of dimension 1 by LOCq(N_A), and global index ja. A copy of these vectors exist on each row of the process grid, and the process column over which the first column of D, E, and tau is distributed is CSRC_A.
9. For suggested block sizes, see Coding Tips for Optimizing Parallel Performance.
10. If lwork = -1 on any process, it must equal -1 on all processes. That is, if a subset of the processes specifies -1 for the work area size, they must all specify -1.

Function

PDSYTRD reduces a real symmetric matrix A to symmetric tridiagonal form T by an orthogonal similarity transformation:

T = Q^TAQ

where:

• A represents the global real symmetric submatrix A_{ia:ia+n-1, ja:ja+n-1}.
• Matrix Q represents the following:
  • For uplo = 'U', the matrix Q is the product of elementary reflectors: Q = H_n-1 ... H₂ H₁,

    where:

    For each i: H_i = I-tauvv^T

    tau is a real scalar

    v is a real vector with v_i+1:n = 0 and v_i = 1

    v_1:i-1 is stored on return in submatrix A_{1+(ia-1):i-1+(ia-1), i+1+(ja-1)}

    tau is stored on return in tau_i+(ja-1)

    I is the identity matrix

    If uplo = 'U', then the following example shows the contents of A on return with n = 5 and ia = ja = 1:

    
    
    

    
    

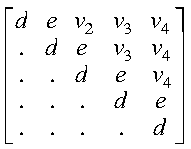
    where:

    d represents the diagonal elements of T

    e represents the superdiagonal elements of T

    v_i represents the corresponding elements of the vector defining H_i.

  • For uplo = 'L', the matrix Q is the product of elementary reflectors: Q = H₁H₂ ... H_n-1,

    where:

    For each i: H_i = I-tauvv^T

    tau is a real scalar

    v is a real vector with v_1:i = 0 and v_i+1 = 1.

    v_i+2:n is stored on return in submatrix A_{i+2+(ia-1):n+(ia-1), i+(ja-1)}.

    tau is stored on return in tau_i+(ja-1)

    I is the identity matrix.

    If uplo = 'L', then the following example shows the contents of A on return with n = 5 and ia = ja = 1:

    
    
    

    
    

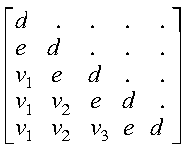
    where:

    d represents the diagonal elements of T

    e represents the subdiagonal elements of T

    v_i represents the corresponding elements of the vector defining H_i.

PZHETRD reduces a complex Hermitian matrix A to symmetric tridiagonal form T by a unitary similarity transformation:

T = Q^HAQ

where:

• A represents the global complex Hermitian submatrix A_{ia:ia+n-1, ja:ja+n-1}.
• Matrix Q represents the following:
  • For uplo = 'U', the matrix Q is the product of elementary reflectors: Q = H_n-1 ... H₂ H₁,

    where:

    For each i: H_i = I-tauvv^T

    tau is a complex scalar

    v is a complex vector with v_i+1:n is (0,0) and v_i is (1,0)

    v_1:i-1 is stored on return in submatrix A_{1+(ia-1):i-1+(ia-1), i+1+(ja-1)}

    tau is stored on return in tau_i+(ja-1)

    I is the identity matrix

    If uplo = 'U', then the following example shows the contents of A on return with n = 5 and ia = ja = 1:

    
    
    

    
    

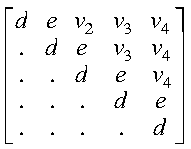
    where:

    d represents the diagonal elements of T

    e represents the superdiagonal elements of T

    v_i represents the corresponding elements of the vector defining H_i.

  • For uplo = 'L', the matrix Q is the product of elementary reflectors: Q = H₁H₂ ... H_n-1,

    where:

    For each i: H_i = I-tauvv^T

    tau is a complex scalar

    v is a complex vector with v_1:i is (0,0) and v_i+1 is (1,0)

    v_i+2:n is stored on return in submatrix A_{i+2+(ia-1):n+(ia-1), i+(ja-1)}

    tau is stored on return in tau_i+(ja-1)

    I is the identity matrix

    If uplo = 'L', then the following example shows the contents of A on return with n = 5 and ia = ja = 1:

    
    
    

    
    

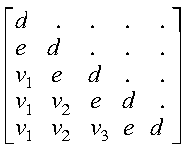
    where:

    d represents the diagonal elements of T

    e represents the subdiagonal elements of T

    v_i represents the corresponding elements of the vector defining H_i.

Error Conditions

Computational Errors

None

Resource Errors

1. lwork = 0 and unable to allocate work space

Input-Argument and Miscellaneous Errors

Stage 1:  

1. DTYPE_A is invalid.

Stage 2:  

1. CTXT_A is invalid.

Stage 3:  

1. This subroutine has been called from outside the process grid.

Stage 4:  

1. uplo <> 'U' or 'L'
2. n < 0
3. M_A < 0 and n = 0; M_A < 1 otherwise
4. N_A < 0 and n = 0; N_A < 1 otherwise
5. MB_A < 1
6. NB_A < 1
7. RSRC_A < 0 or RSRC_A >= p
8. CSRC_A < 0 or CSRC_A >= q
9. ia < 1
10. ja < 1

Stage 5:   If n <> 0:

1. ia > M_A
2. ja > N_A
3. ia+n-1 > M_A
4. ja+n-1 > N_A

In all cases:

1. MB_A <> NB_A
2. mod(ia-1, MB_A) <> 0
3. mod(ja-1, NB_A) <> 0

Stage 6:  

1. LLD_A < max(1, LOCp(M_A))
2. lwork <> 0, lwork <> -1, and lwork < max(nb(np+1), 3nb)

   where:

   nb = MB_A = NB_A

   iarow = mod(RSRC_A+(ia-1)/nb, nprow).

   np = NUMROC(n, nb, myrow, iarow, nprow)

Stage 7:  

Each of the following global input arguments are checked to determine whether its value differs from the value specified on process P₀₀:

1. uplo differs.
2. n differs.
3. ia differs.
4. ja differs.
5. DTYPE_A differs.
6. M_A differs.
7. N_A differs.
8. MB_A differs.
9. NB_A differs.
10. RSRC_A differs.
11. CSRC_A differs.

    Also:

12. lwork = -1 on a subset of processes.

Example 1

This example shows the reduction of a real symmetric matrix of order 4 to symmetric tridiagonal form, using a 2 × 2 process grid.

Note:

Because lwork = 0, PDSYTRD dynamically allocates the work area used by this subroutine.

Call Statements and Input

ORDER = 'R'
NPROW = 2
NPCOL = 2
CALL BLACS_GET(0, 0, ICONTXT)
CALL BLACS_GRIDINIT(ICONTXT, ORDER, NPROW, NPCOL)
CALL BLACS_GRIDINFO(ICONTXT, NPROW, NPCOL, MYROW, MYCOL)
 
              UPLO  N   A   IA  JA   DESC_A   D   E   TAU   WORK  LWORK   INFO
               |    |   |    |   |     |      |   |    |     |      |      |
CALL PDSYTRD( 'U' , 4 , A  , 1 , 1 , DESC_A , D , E , TAU , WORK ,  0   , INFO )

Global real symmetric matrix A of order 4 with block sizes 1 × 1:

B,D     0        1        2        3
     *                                 *
 0   |  5.0  |   4.0  |   1.0  |   1.0 |
     | ------|--------|--------|------ |
 1   |   .   |   5.0  |   1.0  |   1.0 |
     | ------|--------|--------|------ |
 2   |   .   |    .   |   4.0  |   2.0 |
     | ------|--------|--------|------ |
 3   |   .   |    .   |    .   |   4.0 |
     *                                 *

The following is the 2 × 2 process grid:

B,D  |   0 2   | 1 3 
-----| ------- |-----
0    |   P00   |  P01
2    |         |
-----| ------- |-----
1    |   P10   |  P11
3    |         |

Local arrays for A:

p,q  |     0      |      1
-----|------------|------------
 0   |  5.0  1.0  |   4.0  1.0
     |   .   4.0  |    .   2.0
-----|------------|------------
 1   |   .   1.0  |   5.0  1.0
     |   .    .   |    .   4.0

Output:

Global real symmetric matrix A of order 4 with block sizes 1 × 1:

B,D      0         1         2         3
     *                                     *
 0   |  1.00  |   0.00  |   0.41  |   0.22 |
     | -------|---------|---------|------- |
 1   |   .    |   6.00  |   2.83  |   0.22 |
     | -------|---------|---------|------- |
 2   |   .    |    .    |   7.00  |  -2.45 |
     | -------|---------|---------|------- |
 3   |   .    |    .    |    .    |   4.00 |
     *                                     *

The following is the 2 × 2 process grid:

B,D  |   0 2   | 1 3 
-----| ------- |-----
0    |   P00   |  P01
2    |         |
-----| ------- |-----
1    |   P10   |  P11
3    |         |

Local arrays for A:

p,q  |      0       |       1
-----|--------------|--------------
 0   |  1.00  0.41  |   0.00  0.22
     |   .    7.00  |    .   -2.45
-----|--------------|--------------
 1   |   .    2.83  |   6.00  0.22
     |   .     .    |    .    4.00

Global row vector D of length 4 with block size 1:

B,D      0         1         2         3
     *                                     *
 0   |  1.00  |   6.00  |   7.00  |   4.00 |
     *                                     *

Note:

A copy of D is distributed across each row of the process grid.

The following is the 2 × 2 process grid:

B,D  |   0 2   | 1 3 
-----| ------- |-----
     |   P00   |  P01
-----| ------- |-----
     |   P10   |  P11

Local arrays for D:

p,q  |      0       |       1
-----|--------------|--------------
 0   |  1.00  7.00  |   6.00  4.00
-----|--------------|--------------
 1   |  1.00  7.00  |   6.00  4.00

Global row vector E of length 4 with block size 1:

B,D      0         1         2         3
     *                                     *
 0   |  0.00  |   0.00  |   2.83  |  -2.45 |
     *                                     *

Note:

A copy of E is distributed across each row of the process grid.

The following is the 2 × 2 process grid:

B,D  |   0 2   | 1 3 
-----| ------- |-----
     |   P00   |  P01
-----| ------- |-----
     |   P10   |  P11

Local arrays for E:

p,q  |      0       |       1
-----|--------------|--------------
 0   |  0.00  2.83  |   0.00 -2.45
-----|--------------|--------------
 1   |  0.00  2.83  |   0.00 -2.45

Global row vector tau of length 4 with block size 1:

B,D      0         1         2         3
     *                                     *
 0   |  0.00  |   0.00  |   1.71  |   1.82 |
     *                                     *

Note:

A copy of tau is distributed across each row of the process grid.

The following is the 2 × 2 process grid:

B,D  |   0 2   | 1 3 
-----| ------- |-----
     |   P00   |  P01
-----| ------- |-----
     |   P10   |  P11

Local arrays for tau:

p,q  |      0       |       1
-----|--------------|--------------
 0   |  0.00  1.71  |   0.00  1.82
-----|--------------|--------------
 1   |  0.00  1.71  |   0.00  1.82

The value of info is 0 on all processes.

Example 2

This example shows the reduction of a complex Hermitian matrix of order 4 to symmetric tridiagonal form, using a 2 × 2 process grid.

Note:

1. The imaginary parts of the diagonal elements of a complex Hermitian matrix A are assumed to be zero, so you do not have to set these values. On output, they are set to zero, except when n is equal to zero.
2. Because lwork = 0, PZHETRD dynamically allocates the work area used by this subroutine.

ORDER = 'R'
NPROW = 2
NPCOL = 2
CALL BLACS_GET(0, 0, ICONTXT)
CALL BLACS_GRIDINIT(ICONTXT, ORDER, NPROW, NPCOL)
CALL BLACS_GRIDINFO(ICONTXT, NPROW, NPCOL, MYROW, MYCOL)
 
              UPLO  N   A   IA  JA   DESC_A   D   E   TAU   WORK  LWORK   INFO
               |    |   |    |   |     |      |   |    |     |      |      |
CALL PZHETRD( 'L' , 4 , A  , 1 , 1 , DESC_A , D , E , TAU , WORK ,  0   , INFO )

Global complex Hermitian matrix A of order 4 with block sizes 1 × 1:

B,D        0             1            2            3
     *                                                   *
 0   | (5.0, 0.0) |     .      |     .      |     .      |
     |------------|------------|------------|------------|
 1   | (4.0, 1.0) | (5.0, 0.0) |     .      |     .      |
     |------------|------------|------------|------------|
 2   | (1.0, 2.0) | (1.0, 0.0) | (4.0, 0.0) |     .      |
     |------------|------------|------------|------------|
 3   | (2.0, 3.0) | (3.0, 2.0) | (5.0, 1.0) | (4.0, 0.0) |
     *                                                   *

The following is the 2 × 2 process grid:

B,D  |   0 2   | 1 3 
-----| ------- |-----
0    |   P00   |  P01
2    |         |
-----| ------- |-----
1    |   P10   |  P11
3    |         |

Local arrays for A:

p,q  |           0            |            1            
-----|------------------------|------------------------ 
 0   | (5.0,  . )      .      |     .            .      
     | (1.0, 2.0)  (4.0, .  ) | (1.0, 0.0)       .      
-----|------------------------|------------------------ 
 1   | (4.0, 1.0)      .      | (5.0,  . )       .      
     | (2.3, 3.0)  (5.0, 1.0) | (3.0, 2.0)  (4.0,  .  )

Output:

Global complex Hermitian matrix A of order 4 with block sizes 1 × 1:

B,D           0               1              2              3
     *                                                              *
 0   | ( 5.00, 0.00) |       .       |       .      |       .       |
     |---------------|---------------|--------------|---------------|
 1   | (-5.92, 0.00) | (10.09, 0.00) |       .      |       .       |
     |---------------|---------------|--------------|---------------|
 2   | ( 0.12, 0.19) | ( 2.36, 0.00) | ( 4.16, 0.0) |       .       |
     |---------------|---------------|--------------|---------------|
 3   | ( 0.23, 0.28) | ( 0.14, 0.19) | ( 1.62, 0.00)| (-1.25, 0.00) |
     *                                                              *

The following is the 2 × 2 process grid:

B,D  |   0 2   | 1 3 
-----| ------- |-----
0    |   P00   |  P01
2    |         |
-----| ------- |-----
1    |   P10   |  P11
3    |         |

Local arrays for A

p,q  |              0               |                1            
-----|------------------------------|-----------------------------
 0   | ( 5.00, 0.00)        .       |       .              .      
     | ( 0.12, 0.19)  ( 4.16, 0.00) | ( 2.36, 0.00)        .      
-----|------------------------------|-----------------------------
 1   | (-5.92, 0.00)        .       | (10.09, 0.00)        .      
     | ( 0.23, 0.28)  ( 1.62, 0.00) | ( 0.14, 0.19)  (-1.25, 0.00)

Global row vector D of length 4 with block size 1:

B,D      0         1         2         3
     *                                     *
 0   |  5.00  |  10.09  |   4.16  |  -1.25 |
     *                                     *

Note:

A copy of D is distributed across each row of the process grid.

The following is the 2 × 2 process grid:

B,D  |   0 2   | 1 3 
-----| ------- |-----
     |   P00   |  P01
-----| ------- |-----
     |   P10   |  P11

Local arrays for D:

p,q  |      0       |       1
-----|--------------|--------------
 0   |  5.00  4.16  |  10.09  -1.25
-----|--------------|--------------
 1   |  5.00  4.16  |  10.09  -1.25

Global row vector E of length 4 with block size 1:

B,D       0         1         2         3
     *                                    *
 0   |  -5.92  |   2.36  |  1.62  |  0.00 |
     *                                    *

Note:

A copy of E is distributed across each row of the process grid.

The following is the 2 × 2 process grid:

B,D  |   0 2   | 1 3 
-----| ------- |-----
     |   P00   |  P01
     |         |
-----| ------- |-----
     |   P10   |  P11
     |         |

Local arrays for E:

p,q  |      0       |       1
-----|--------------|--------------
 0   | -5.92  1.62  |   2.36  0.00 
-----|--------------|--------------
 1   | -5.92  1.62  |   2.36  0.00

Global row vector tau of length 4 with block size 1:

B,D          0              1             2              3
     *                                                            *
 0   | (1.68, 0.17) | (1.87, 0.21) | (1.96, -0.27) | (0.00, 0.00) |
     *                                                            *

Note:

A copy of tau is distributed across each row of the process grid.

The following is the 2 × 2 process grid:

B,D  |   0 2   | 1 3 
-----| ------- |-----
     |   P00   |  P01
-----| ------- |-----
     |   P10   |  P11

Local arrays for tau:

p,q  |             0              |             1
-----|----------------------------|--------------------------
 0   | (1.68, 0.17) (1.96, -0.27) | (1.87, 0.21) (0.00, 0.00)
-----|----------------------------|--------------------------
 1   | (1.68, 0.17) (1.96, -0.27) | (1.87, 0.21) (0.00, 0.00)

The value of info is 0 on all processes.