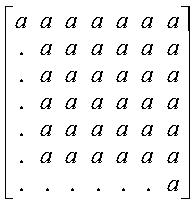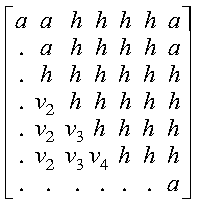Parallel Engineering and Scientific Subroutine Library for AIX Version 2 Release 3: Guide and Reference

PDGEHRD--Reduce a General Matrix to Upper Hessenberg Form

This subroutine reduces a real general matrix A to upper Hessenberg form H by an orthogonal similarity transformation:

H = Q^TAQ

where A represents the global general submatrix A_{ia+ilo-1:
ia+ihi-1, ja+ilo-1:
ja+ihi-1}.

If n = 0, no computation is performed, and the subroutine returns after doing some parameter checking. Then, if ihi = ilo, the subroutine returns after doing some parameter checking and setting tau_ja:ja+ilo-2 and tau_{ja+ihi-1:ja+n-2} to zero.

See references [13] and [21].

Table 106. Data Types

A, tau, `work`	Subroutine
Long-precision real	PDGEHRD

Syntax

Fortran	CALL PDGEHRD (`n`, `ilo`, `ihi`, `a`, `ia`, `ja`, `desc_a`, `tau`, `work`, `lwork`, `info`)
C and C++	pdgehrd (`n`, `ilo`, `ihi`, `a`, `ia`, `ja`, `desc_a`, `tau`, `work`, `lwork`, `info`);

On Entry

n

is the order of submatrix A used in the computation.

Scope: global

Specified as: a fullword integer; n >= 0.

ilo

lower range of the rows or columns in the global general submatrix A used in the computation.

Scope: global

Specified as: a fullword integer; 1 <= ilo <= max(1, n).

ihi

upper range of the rows or columns in the global general submatrix A used in the computation.

Scope: global

Specified as: a fullword integer; min(ilo, n) <= ihi <= n.

a

is the local part of the global general matrix A. This identifies the first element of the local array A. This subroutine computes the location of the first element of the local subarray used, based on ia, ja, desc_a, p, q, myrow, and mycol; therefore, the leading LOCp(ia+n-1) by LOCq(ja+n-1) part of the local array A must contain the local pieces of the leading ia+n-1 by ja+n-1 part of the global matrix.

Scope: local

Specified as: an LLD_A by (at least) LOCq(N_A) array, containing numbers of the data type indicated in Table 106. Details about the square block-cyclic data distribution of global matrix A are stored in desc_a.

ia

is the row index of the global matrix A, identifying the first row of the submatrix A.

Scope: global

Specified as: a fullword integer; 1 <= ia <= M_A and ia+n-1 <= M_A.

ja

is the column index of the global matrix A, identifying the first column of the submatrix A.

Scope: global

Specified as: a fullword integer; 1 <= ja <= N_A and ja+n-1 <= N_A.

desc_a

is the array descriptor for global matrix A, described in the following table:

`desc_a`	Name	Description	Limits	Scope
1	DTYPE_A	Descriptor type	DTYPE_A=1	Global
2	CTXT_A	BLACS context	Valid value, as returned by BLACS_GRIDINIT or BLACS_GRIDMAP	Global
3	M_A	Number of rows in the global matrix	If `n` = 0: M_A >= 0 Otherwise: M_A >= 1	Global
4	N_A	Number of columns in the global matrix	If `n` = 0: N_A >= 0 Otherwise: N_A >= 1	Global
5	MB_A	Row block size	MB_A >= 1	Global
6	NB_A	Column block size	NB_A >= 1	Global
7	RSRC_A	The process row of the `p` × `q` grid over which the first row of the global matrix is distributed	0 <= RSRC_A < `p`	Global
8	CSRC_A	The process column of the `p` × `q` grid over which the first column of the global matrix is distributed	0 <= CSRC_A < `q`	Global
9	LLD_A	The leading dimension of the local array	LLD_A >= max(1,LOCp(M_A))	Local

Specified as: an array of (at least) length 9, containing fullword integers.

tau

See On Return.

work

has the following meaning:

If lwork = 0, work is ignored.

If lwork <> 0, work is the work area used by this subroutine, where:

If lwork <> -1, its size is (at least) of length lwork.
If lwork = -1, its size is (at least) of length 1.

Scope: local

Specified as: an area of storage containing numbers of data type indicated in Table 106.

lwork

is the number of elements in array WORK.

Scope:

If lwork >= 0, lwork is local
If lwork = -1, lwork is global

Specified as: a fullword integer; where:

If lwork = 0, PDGEHRD dynamically allocates the work area used by this subroutine. The work area is deallocated before control is returned to the calling program. This option is an extension to the ScaLAPACK standard.
If lwork = -1, PDGEHRD performs a work area query and returns the minimum size of work in work₁. No computation is performed and the subroutine returns after error checking is complete.
Otherwise, it must have the following value:
lwork >= (nb × nb)+nb × max(ihip+1, ihlp+inlq)
where:

nb = MB_A = NB_A
ioff = mod(ia+ilo-2, nb)
iroffa = mod(ia-1, nb)
iarow = mod(RSRC_A+(ia-1)/nb, nprow)
ilrow = mod(RSRC_A+(ia+ilo-2)/nb, nprow)
ilcol = mod(CSRC_A+(ja+ilo-2)/nb, npcol)
ihip = NUMROC(ihi+iroffa, nb, myrow, iarow, nprow)
ihlp = NUMROC(ihi-ilo+ioff+1, nb, myrow, ilrow, nprow)
inlq = NUMROC(n-ilo+ioff+1, nb, mycol, ilcol, npcol)

info

See On Return.

On Return

a

is the updated local part of the global general matrix A, containing the results of the computation.

The upper triangle and the first subdiagonal of A_{ia:ia+n-1,
ja:ja+n-1} are overwritten by the corresponding elements of the upper Hessenberg matrix H. The elements below the first subdiagonal are overwritten with v_i+2:ihi. These elements with tau represent the orthogonal matrix Q as a product of elementary reflectors.

See Function, for more information.

Scope: local

Returned as: an LLD_A by (at least) LOCq(N_A) array, containing numbers of the data type indicated in Table 106. Details about the square block-cyclic data distribution of global matrix A are stored in desc_a.

tau

is the updated local part of the global matrix tau, where:

tau_{ja+ilo-1:ja+ihi-2} contains the scalar factors of the elementary reflectors.
tau_ja:ja+ilo-2 are set to zero.
tau_{ja+ihi-1:ja+n-2} are set to zero.

This identifies the first element of the local array tau. This subroutine computes the location of the first element of the local subarray used, based on ja, desc_a, p, q, myrow, and mycol; therefore, the leading 1 by LOCq(ja+n-2) part of the local array tau must contain the local pieces of the leading 1 by ja+n-2 part of the global matrix tau.

A copy of the vector tau, with a block size of NB_A and global index ja, is returned to each row of the process grid. The process column over which the first column of tau is distributed is CSRC_A.

Scope: local

Returned as: a 1 by (at least) LOCq(N_A-1) array, containing numbers of the data type indicated in Table 106.

work

is the work area used by this subroutine if lwork <> 0, where:

If lwork <> 0 and lwork <> -1, its size is (at least) of length lwork.

If lwork = -1, its size is (at least) of length 1.

Scope: local

Returned as: an area of storage, where:

If lwork >= 1 or lwork = -1, then work₁ is set to the minimum lwork value and contains numbers of the data type indicated in Table 106. Except for work₁, the contents of work are overwritten on return.

info

indicates that a successful computation occurred.

Scope: global

Returned as: a fullword integer; info = 0.

Notes and Coding Rules

In your C program, argument info must be passed by reference.
Matrix A, tau, and work must have no common elements; otherwise, results are unpredictable.
On entry, the general submatrix A_{ia:ia+n-1,
ja:ja+n-1} must already be upper triangular in rows (ia:ia+ilo-2) and (ia+ihi:ia+n-1), and upper triangular in columns (ja:ja+ilo-2) and (ja+ihi:ja+n-1). If this is not the case, you should set ilo = 1 and ihi = n.
If n = 0, you should set ilo = 1 and ihi = 0. If n > 0, you should set 1 <= ilo <= ihi <= n.
The NUMROC utility subroutine can be used to determine the values of LOCp(M_) and LOCq(N_) used in the argument descriptions above. For details, see Determining the Number of Rows and Columns in Your Local Arrays and NUMROC--Compute the Number of Rows or Columns of a Block-Cyclically Distributed Matrix Contained in a Process.
The global general matrix A must be distributed using a square block-cyclic distribution; that is, MB_A = NB_A.
The global general matrix A must be aligned on a block boundary; that is:
- ia-1 must be a multiple of MB_A
- ja-1 must be a multiple of NB_A
There is no array descriptor for tau. tau is a row-distributed vector with block size NB_A, local arrays of dimension 1 by LOCq(N_A-1), and global index ja. A copy of tau exists on each row of the process grid, and the process column over which the first column of tau is distributed is CSRC_A.
For suggested block sizes, see Coding Tips for Optimizing Parallel Performance.
If lwork = -1 on any process, it must equal -1 on all processes. That is, if a subset of the processes specifies -1 for the work area size, they must all specify -1.

Function

This subroutine reduces a real general matrix A to upper Hessenberg form H by an orthogonal similarity transformation:

H = Q^TAQ

where:

A represents the global general submatrix A_{ia+ilo-1:ia+ihi-1,
ja+ilo-1:ja+ihi-1}
Matrix Q is represented as a product of (ihi-ilo) elementary reflectors:

Q = H_ilo H_ilo+1 ... H_ihi-1

where:

For each i: H_i = I-tauvv^T
tau is a real scalar
v is a real vector with v_1:i = 0, v_i+1 = 1, and v_ihi+1:n = 0
v_i+2:ihi is stored on return in in submatrix A_{i+ilo+1+(ia-1):ihi+(ia-1),
ilo+i-1+(ja-1)}
tau is stored on return in tau_{i+ilo-1+(ja-1)}
I is the identity matrix

The following example shows the contents of the general submatrix A on entry with n = 7, ia = ja = 1, ilo = 2, and ihi = 6:

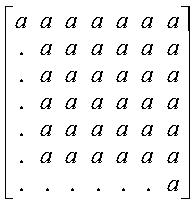
Following is the general submatrix A on return:

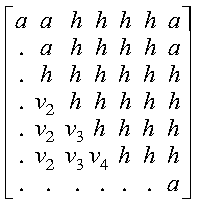
where:

a represents an element of the original submatrix A.
h represents a updated element of the upper Hessenberg matrix H.
v_i represents the corresponding elements of the vector defining H_{ilo+i-1+(ja-1)}.

Error Conditions

Computational Errors

None

Resource Errors

lwork = 0 and unable to allocate work space

Input-Argument and Miscellaneous Errors

Stage 1:

DTYPE_A is invalid.

Stage 2:

CTXT_A is invalid.

Stage 3:

PDGEHRD has been called from outside the process grid.

Stage 4:

n < 0
M_A < 0 and n = 0; M_A < 1 otherwise
N_A < 0 and n = 0; N_A < 1 otherwise
MB_A < 1
NB_A < 1
RSRC_A < 0 or RSRC_A >= p
CSRC_A < 0 or CSRC_A >= q
ia < 1
ja < 1

Stage 5:

ilo < 1 or ilo > max(1, n)
ihi < min(ilo, n) or ihi > n

If n <> 0:

ia > M_A
ja > N_A
ia+n-1 > M_A
ja+n-1 > N_A

In all cases:

MB_A <> NB_A
mod(ia-1, MB_A) <> 0
mod(ja-1, NB_A) <> 0

Stage 6:

LLD_A < max(1, LOCp(M_A))
lwork <> 0, lwork <> -1, and lwork < (nb × nb)+nb × max(ihip+1, ihlp+inlq)
where:

nb = MB_A = NB_A
ioff = mod(ia+ilo-2, nb)
iroffa = mod(ia-1, nb)
iarow = mod(RSRC_A+(ia-1)/nb, nprow)
ilrow = mod(RSRC_A+(ia+ilo-2)/nb, nprow)
ilcol = mod(CSRC_A+(ja+ilo-2)/nb, npcol)
ihip = NUMROC(ihi+iroffa, nb, myrow, iarow, nprow)
ihlp = NUMROC(ihi-ilo+ioff+1, nb, myrow, ilrow, nprow)
inlq = NUMROC(n-ilo+ioff+1, nb, mycol, ilcol, npcol)

Stage 7:

Each of the following global input arguments are checked to determine whether its value differs from the value specified on process P₀₀:

n differs.
ilo differs.
ihi differs.
ia differs.
ja differs.
DTYPE_A differs.
M_A differs.
N_A differs.
MB_A differs.
NB_A differs.
RSRC_A differs.
CSRC_A differs.

Also:
lwork = -1 on a subset of processes.

Example

This example shows the reduction of a general matrix of order 3 to upper Hessenberg form using a 2 × 2 process grid.

Note:: Because lwork = 0, PDGEHRD dynamically allocates the work area used by this subroutine.

Call Statements and Input

ORDER = 'R'
NPROW = 2
NPCOL = 2
CALL BLACS_GET(0, 0, ICONTXT)
CALL BLACS_GRIDINIT(ICONTXT, ORDER, NPROW, NPCOL)
CALL BLACS_GRIDINFO(ICONTXT, NPROW, NPCOL, MYROW, MYCOL)
 
              N   ILO   IHI   A  IA  JA   DESC_A   TAU   WORK   LWORK   INFO
              |    |     |    |   |   |     |       |     |       |      |
CALL PDGEHRD( 3 ,  1  ,  3  , A , 1 , 1 , DESC_A , TAU , WORK  ,  0   , INFO)

	DESC_A
DTYPE_	1
CTXT_	`icontxt`^(IITOOT5)
M_	3
N_	3
MB_	1
NB_	1
RSRC_	0
CSRC_	0
LLD_	See below^(EPSSTL5)
Notes: `icontxt` is the output of the BLACS_GRIDINIT call. Each process should set the LLD_ as follows: LLD_A = MAX(1,NUMROC(M_A, MB_A, MYROW, RSRC_A, NPROW)) In this example, LLD_A = 2 on P₀₀ and P₀₁, and LLD_A = 1 on P₁₀ and P₁₁.

Global general matrix A of order 3 with block sizes 1 × 1:

B,D      0         1         2
     *                           *
 0   |  33.0  |   16.0  |   72.0 |
     | -------|---------|------- |
 1   | -24.0  |  -10.0  |  -57.0 |
     | -------|---------|------- |
 2   |  -8.0  |   -4.0  |  -17.0 |
     *                           *

The following is the 2 × 2 process grid:

B,D  |  0 2  | 1 
-----|-------|-----
0    |   P₀₀   |  P₀₁
2    |       |
-----|-------|-----
1    |   P₁₀   |  P₁₁

Local arrays for A:

p,q  |      0       |    1
-----|--------------|--------
 0   |  33.0  72.0  |   16.0
     |  -8.0 -17.0  |   -4.0
-----|--------------|--------
 1   | -24.0 -57.0  |  -10.0

Output:

Global general matrix A of order 3 with block sizes 1 × 1:

B,D      0          1          2
     *                              *
 0   |  33.00  |  -37.95  |   63.25 |
     | --------|----------|-------- |
 1   |  25.30  |  -29.00  |   53.00 |
     | --------|----------|-------- |
 2   |   0.16  |    0.00  |    2.00 |
     *                              *

The following is the 2 × 2 process grid:

B,D  |  0 2  | 1 
-----|-------|-----
0    |   P₀₀   |  P₀₁
2    |       |
-----|-------|-----
1    |   P₁₀   |  P₁₁

Local arrays for A:

p,q  |       0        |    1
-----|----------------|---------
 0   |  33.0   63.25  |  -37.95
     |   0.16   2.00  |    0.00
-----|----------------|---------
 1   |  25.30  53.00  |  -29.00

Global row vector tau of length 2 with block sizes of 1:

B,D      0         1
     *                 *
 0   |  1.95  |   0.00 |
     *                 *

Note:: A copy of tau is distributed across each row of the process grid.

The following is the 2 × 2 process grid:

B,D  |   0   | 1 
-----|-------|-----
     |   P₀₀   |  P₀₁
-----|-------|-----
     |   P₁₀   |  P₁₁

Local arrays for tau:

p,q  |   0    |    1
-----|--------|--------
 0   |  1.95  |   0.00
-----|--------|--------
 1   |  1.95  |   0.00

The value of info is 0 on all processes.

[ Top of Page | Previous Page | Next Page | Table of Contents | Index ]