Parallel Engineering and Scientific Subroutine Library for AIX Version 2 Release 3: Guide and Reference

PSRCFT2 and PDRCFT2--Real-to-Complex Fourier Transforms in Two Dimensions

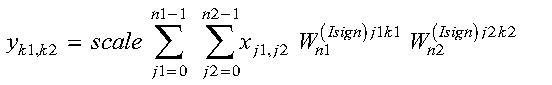
These subroutines compute the mixed-radix two-dimensional complex conjugate even discrete Fourier transform of real data:

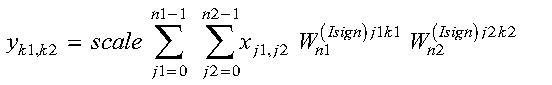
FFT Graphic

for:

k1 = 0, 1, ..., n1-1

k2 = 0, 1, ..., n2-1

where:

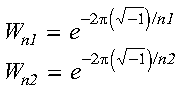
FFT Graphic

and where:

x_j1,j2 are elements of array X.

y_k1,k2 are elements of array Y.

Isign is + or - (determined by argument isign).

scale is a scalar value.

For scale = 1 and isign being positive, you obtain the discrete Fourier transform. For scale = 1/((n1)(n2)) and isign being negative, you obtain the inverse Fourier transform.

See references [1] and [3].

Table 110. Data Types

`X`, `scale`	`Y`	Subroutine
Short-precision real	Short-precision complex	PSRCFT2
Long-precision real	Long-precision complex	PDRCFT2

is the local array X, containing the two-dimensional data to be transformed that has been block-column distributed over a 1 × q process grid, where q is the number of processes. (The value of ldx is set in the IP array.)

Scope: local

Specified as: an array of (at least) length ldx × LOCq(n2), containing numbers of the data type indicated in Table 110. This array must be aligned on a doubleword boundary.

y

See On Return.

n1

is the length of the first dimension of the two-dimensional data in the array to be transformed.

Scope: global

Specified as: a fullword integer; n1 <= 37748736 and must be one of the values listed in Figure 9.

n2

is the length of the second dimension of the two-dimensional data in the array to be transformed.

Scope: global

Specified as: a fullword integer; n2 <= 37748736 and must be one of the values listed in Figure 9.

isign

controls the direction of the transform, determining the sign, isign, of the exponent of W_n, where:

If isign = positive value, Isign = + (transforming time to frequency).

If isign = negative value, Isign = - (transforming frequency to time).

Scope: global

Specified as: a fullword integer; where isign > 0 or isign < 0.

scale

is the scaling constant scale.

Scope: global

Specified as: a number of the data type indicated in Table 110, where scale > 0.0 or scale < 0.0.

icontxt

is the BLACS context parameter.

Scope: global

Specified as: the fullword integer that was returned by a prior call to BLACS_GRIDINIT or BLACS_GRIDMAP.

ip

is an array of parameters, IP(i), where:

IP(1) indicates whether the default values for ip are used or you set the values for ip.
If IP(1) = 0, then the following default values are used:
- ldx, the leading dimension of the array specified for X, equals n1
- ldy, the leading dimension of the array specified for Y, equals n2
The remaining parameters of the array IP are ignored.
If IP(1) <> 0, then you set the remaining values of ip to indicate values for ldx and ldy.
IP(2-19) are reserved.
IP(20) indicates the value of the leading dimension, ldx, of the array specified for X, where:
If IP(20) = 0, then ldx = n1.
If IP(20) <> 0, then ldx is this value of IP(20).
IP(21) indicates the value of the leading dimension, ldy, of the array specified for Y, where:
If IP(21) = 0, then ldy = n2.
If IP(21) <> 0, then ldy is this value of IP(21).
IP(22-40) are reserved.

Scope: global

Specified as: a one-dimensional array of (at least) length 40, containing fullword integers, where:

IP(1) is any integer

IP(20) >= n1 or IP(20) = 0

IP(21) >= n2 or IP(21) = 0

On Return

y

is the local array Y, stored in FFT-packed storage mode, containing the results of the computation that are block-column distributed, where:

If IP(1) = 0, the local array Y has dimensions n2 × LOCq(n1/2).

If IP(1) <> 0 and IP(21) = 0, the local array Y has dimensions n2 × LOCq(n1/2).

If IP(1) <> 0 and IP(21) <> 0, the local array Y has dimensions ldy × LOCq(n1/2).

Scope: local

Returned as: an ldy × LOCq(n1/2) array, containing the numbers of the data type indicated in Table 110. This array must be aligned on a doubleword boundary.

Notes and Coding Rules

These subroutines always return Y in transposed form.
For the output array Y, these subroutines may use any extra space available when ldy is greater than its minimum value.
You may specify the same array for X and Y. In this case, output overwrites input. If you specify different arrays X and Y, they must have no common elements; otherwise, results are unpredictable.
For more information on LOCq(_), and how sequences are block-column distributed and stored in FFT-packed storage mode, see Two-Dimensional Sequence.
In general, distributing your data evenly provides the best work load balance among the processes and allows the use of the most efficient collective communication. However, for your specific problem size and number of processes available, experimentation is necessary to achieve optimal performance.

Error Conditions

Computational Errors

None

Resource Errors

Unable to allocate work space

Input-Argument and Miscellaneous Errors

Stage 1:

icontxt is invalid

Stage 2:

Process grid is not 1 × q
The subroutine was called from outside the process grid.

Stage 3:

n1 > 37748736
n2 > 37748736
The length of n1 or n2 is not an allowable transform length.
isign = 0
scale = 0.0
IP(1) <> 0 and IP(20) <> 0 and IP(20) < n1 (that is, ldx < n1)
IP(1) <> 0 and IP(21) <> 0 and IP(21) < n2 (that is, ldy < n2)

Example

This example shows how to compute a two-dimensional transform. The data is block-column distributed over a 1 × 2 process grid. The arrays are declared as follows:

  REAL*8 X(0:11,0:1)
  COMPLEX*16 Y(0:6,0:1)
  INTEGER*4 IP(40)
  REAL*8 SCALE

Call Statements and Input

ORDER = 'R'
NPROW = 1
NPCOL = 2
CALL BLACS_GET(0, 0, ICONTXT)
CALL BLACS_GRIDINIT(ICONTXT, ORDER, NPROW, NPCOL)
CALL BLACS_GRIDINFO(ICONTXT, NPROW, NPCOL, MYROW, MYCOL)
IP(1) = 1
IP(20) = 12 (that is, ldx = 12)
IP(21) = 7  (that is, ldy = 7)
 
              X   Y   N1  N2  ISIGN  SCALE   ICONTXT   IP
              |   |   |   |     |      |        |      |
CALL PDRCFT2( X , Y , 8 , 4 ,   1  , 1.0D0 , ICONTXT , IP)

Global matrix X of order 8 × 4:

B,D        0              1
     *                          *
     |  1.0   0.0  |   0.0  0.0 |
     |  0.0   0.0  |   0.0  0.0 |
     |  0.0   0.0  |   0.0  0.0 |
     |  0.0   0.0  |   0.0  0.0 |
     |  0.0   0.0  |   0.0  0.0 |
     |  0.0   0.0  |   0.0  0.0 |
 0   |  0.0   0.0  |   0.0  0.0 |
     |  0.0   0.0  |   0.0  0.0 |
     |   .     .   |    .    .  |
     |   .     .   |    .    .  |
     |   .     .   |    .    .  |
     |   .     .   |    .    .  |
     *                          *

The following is the 1 × 2 process grid:

B,D  |   0   | 1 
-----|-------|-----
0    |   P₀₀   |  P₀₁

Local arrays for X:

p,q  |     0      |      1
-----|------------|------------
     |  1.0  0.0  |   0.0  0.0
     |  0.0  0.0  |   0.0  0.0
     |  0.0  0.0  |   0.0  0.0
     |  0.0  0.0  |   0.0  0.0
     |  0.0  0.0  |   0.0  0.0
     |  0.0  0.0  |   0.0  0.0
 0   |  0.0  0.0  |   0.0  0.0
     |  0.0  0.0  |   0.0  0.0
     |   .    .   |    .    .
     |   .    .   |    .    .
     |   .    .   |    .    .
     |   .    .   |    .    .

Output

The following global matrix Y is returned in transposed form and stored in FFT-packed storage mode:

B,D              0                          1
     *                                                   *
     |  (1.0,1.0)  (1.0,0.0)  |     (1.0,0.0)  (1.0,0.0) |
     |  (1.0,0.0)  (1.0,0.0)  |     (1.0,0.0)  (1.0,0.0) |
     |  (1.0,1.0)  (1.0,0.0)  |     (1.0,0.0)  (1.0,0.0) |
 0   |  (1.0,0.0)  (1.0,0.0)  |     (1.0,0.0)  (1.0,0.0) |
     |      .          .      |         .          .     |
     |      .          .      |         .          .     |
     |      .          .      |         .          .     |
     *                                                   *

The following is the 1 × 2 process grid:

B,D  |   0   | 1 
-----|-------|-----
0    |   P₀₀   |  P₀₁

The following local arrays for Y are returned in transposed form and stored in FFT-packed storage mode:

p,q  |           0             |            1
-----|-------------------------|-------------------------
     |  (1.0,1.0)   (1.0,0.0)  |   (1.0,0.0)   (1.0,0.0)
     |  (1.0,0.0)   (1.0,0.0)  |   (1.0,0.0)   (1.0,0.0)
     |  (1.0,1.0)   (1.0,0.0)  |   (1.0,0.0)   (1.0,0.0)
 0   |  (1.0,0.0)   (1.0,0.0)  |   (1.0,0.0)   (1.0,0.0)
     |      .           .      |       .           .
     |      .           .      |       .           .
     |      .           .      |       .           .

[ Top of Page | Previous Page | Next Page | Table of Contents | Index ]

Fortran	CALL PSRCFT2 \| PDRCFT2 (`x`, `y`, `n1`, `n2`, `isign`, `scale`, `icontxt`, `ip`)
C and C++	psrcft2 \| pdrcft2 (`x`, `y`, `n1`, `n2`, `isign`, `scale`, `icontxt`, `ip`);

Parallel Engineering and Scientific Subroutine Library for AIX Version 2 Release 3: Guide and Reference

PSRCFT2 and PDRCFT2--Real-to-Complex Fourier Transforms in Two Dimensions

Syntax

On Entry

On Return

Notes and Coding Rules

Error Conditions

Computational Errors

Resource Errors

Input-Argument and Miscellaneous Errors

Example

Call Statements and Input

Output