Parallel Engineering and Scientific Subroutine Library for AIX Version 2 Release 3: Guide and Reference

PSCRFT3 and PDCRFT3--Complex-to-Real Fourier Transforms in Three Dimensions

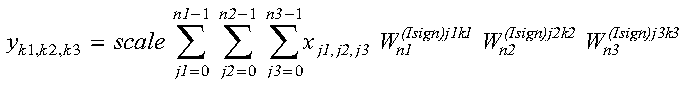
These subroutines compute the mixed-radix three-dimensional real discrete Fourier transform of complex conjugate even data:

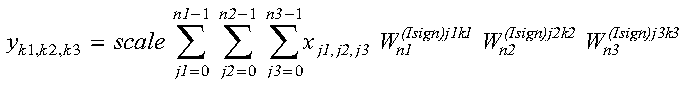
for:

k1 = 0, 1, ..., n1-1

k2 = 0, 1, ..., n2-1

k3 = 0, 1, ..., n3-1

where:

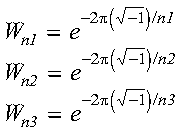
and where:

x_j1,j2,j3 are elements of array X.

y_k1,k2,k3 are elements of array Y.

Isign is + or - (determined by argument isign).

scale is a scalar value.

See references [1] and [3].

Table 114. Data Types

Syntax

On Entry

x

is the local array X, containing the three-dimensional data to be transformed that has been block-plane distributed over a 1 × q process grid, where q is the number of processes. (The value of ldx1 and ldx2 are set in the IP array.) Array X is stored in FFT-packed storage mode.

Scope: local

Specified as: an array of (at least) length ldx1 × ldx2 × LOCq(n1/2), containing numbers of the data type indicated in Table 114. This array must be aligned on a doubleword boundary.

y

See On Return.

n1

is the length of the first dimension of the three-dimensional data in the array to be transformed.

Scope: global

Specified as: a fullword integer; n1 <= 37748736 and must be one of the values listed in Figure 9.

n2

is the length of the second dimension of the three-dimensional data in the array to be transformed.

Scope: global

Specified as: a fullword integer; n2 <= 37748736 and must be one of the values listed in Figure 9.

n3

is the length of the third dimension of the three-dimensional data in the array to be transformed.

Scope: global

Specified as: a fullword integer; n3 <= 37748736 and must be one of the values listed in Figure 9.

isign

controls the direction of the transform, determining the sign, isign, of the exponent of W_n, where:

If isign = positive value, Isign = + (transforming time to frequency).

If isign = negative value, Isign = - (transforming frequency to time).

Scope: global

Specified as: a fullword integer; where isign > 0 or isign < 0.

scale

is the scaling constant scale.

Scope: global

Specified as: a number of the data type indicated in Table 114, where scale > 0.0 or scale < 0.0.

icontxt

is the BLACS context parameter.

Scope: global

Specified as: the fullword integer that was returned by a prior call to BLACS_GRIDINIT or BLACS_GRIDMAP.

ip

is an array of parameters, IP(i), where:

• IP(1) indicates whether the default values for ip are used or you set the values for ip.

  If IP(1) = 0, then the following default values are used:

  • ldx1 and ldx2, the leading dimensions of the array specified for X, equal n3 and n2, respectively.
  • ldy1 and ldy2, the leading dimensions of the array specified for Y, equal n1 and n2, respectively.

  The remaining parameters of the array IP are ignored.

  If IP(1) <> 0, then you set the remaining values of ip to indicate values for the leading dimensions.

• IP(2-19) are reserved.
• IP(20) indicates the value of the leading dimension, ldx1, of the array specified for X, where:

  If IP(20) = 0, then ldx1 = n3.

  If IP(20) <> 0, then ldx1 is this value of IP(20).

• IP(21) indicates the value of the leading dimension, ldx2, of the array specified for X, where:

  If IP(21) = 0, then ldx2 = n2.

  If IP(21) <> 0, then ldx2 is this value of IP(21).

• IP(22) indicates the value of the leading dimension, ldy1, of the array specified for Y, where:

  If IP(22) = 0, then ldy1 = n1.

  If IP(22) <> 0, then ldy1 is this value of IP(22).

• IP(23) indicates the value of the leading dimension, ldy2, of the array specified for Y, where:

  If IP(23) = 0, then ldy2 = n2.

  If IP(23) <> 0, then ldy2 is this value of IP(23).

• IP(24-40) are reserved.

Scope: global

Specified as: a one-dimensional array of (at least) length 40, containing fullword integers, where:

IP(1) is any integer

IP(20) >= n3 or IP(20) = 0

IP(21) >= n2 or IP(21) = 0

IP(22) >= n1 or IP(22) = 0

IP(23) >= n2 or IP(23) = 0

On Return

y

is the local array Y that is block-plane distributed and contains the results of the computation, where:

If IP(1) = 0, the local array Y has dimensions n1 × n2 × LOCq(n3).

If IP(1) <> 0, the local array Y has dimensions ldy1 × ldy2 × LOCq(n3).

Scope: local

Returned as: an ldy1 × ldy2 × LOCq(n3) array, containing the numbers of the data type indicated in Table 114. This array must be aligned on a doubleword boundary.

Notes and Coding Rules

1. These subroutines always return Y in normal form.
2. For the output array Y, these subroutines may use any extra space available when ldy1 and ldy2 are greater than their minimum value.
3. You may specify the same array for X and Y. In this case, output overwrites input. If you specify different arrays X and Y, they must have no common elements; otherwise, results are unpredictable.
4. For more information on LOCq(_), and how sequences are block-plane distributed and stored in FFT-packed storage mode, see Three-Dimensional Sequences.

   In general, distributing your data evenly provides the best work load balance among the processes and allows the use of the most efficient collective communication. However, for your specific problem size and number of processes available, experimentation is necessary to achieve optimal performance.

Error Conditions

Computational Errors

None

Resource Errors

1. Unable to allocate work space

Input-Argument and Miscellaneous Errors

Stage 1:  

1. icontxt is invalid

Stage 2:  

1. Process grid is not 1 × q
2. The subroutine was called from outside the process grid.

Stage 3:  

1. n1 > 37748736
2. n2 > 37748736
3. n3 > 37748736
4. The length of n1, n2, n3 is not an allowable transform length.
5. isign = 0
6. scale = 0.0
7. IP(1) <> 0 and IP(20) <> 0 and IP(20) < n3 (that is, ldx1 < n3)
8. IP(1) <> 0 and IP(21) <> 0 and IP(21) < n2 (that is, ldx2 < n2)
9. IP(1) <> 0 and IP(22) <> 0 and IP(22) < n1 (that is, ldy1 < n1)
10. IP(1) <> 0 and IP(23) <> 0 and IP(23) < n2 (that is, ldy2 < n2)

Example

This example shows how to compute a three-dimensional transform. The data is block-plane distributed over a 1 × 2 process grid. The arrays are declared as follows:

  COMPLEX*16 X(0:4,0:3,0)
  REAL*8 Y(0:8,0:3,0:1)
  INTEGER*4 IP(40)
  REAL*8 SCALE

Call Statements and Input

ORDER = 'R'
NPROW = 1
NPCOL = 2
CALL BLACS_GET(0, 0, ICONTXT)
CALL BLACS_GRIDINIT(ICONTXT, ORDER, NPROW, NPCOL)
CALL BLACS_GRIDINFO(ICONTXT, NPROW, NPCOL, MYROW, MYCOL)
SCALE = 1.0D0/4*4*4
IP(1) = 1
IP(20) = 5
IP(21) = 4
IP(22) = 9
IP(23) = 4
 
              X   Y   N1  N2  N3  ISIGN      SCALE      ICONTXT   IP
              |   |   |   |   |     |          |           |      |
CALL PDCRFT3( X , Y , 4 , 4 , 4  , -1  , 1.0D0/64.0D0 , ICONTXT , IP)

The following global matrix X is stored in FFT-packed storage mode:

Plane 0:

B,D                         0
     *                                             *
     |  (1.0,1.0)  (1.0,0.0)  (1.0,1.0)  (1.0,0.0) |
     |  (1.0,0.0)  (1.0,0.0)  (1.0,0.0)  (1.0,0.0) |
 0   |  (1.0,1.0)  (1.0,0.0)  (1.0,1.0)  (1.0,0.0) |
     |  (1.0,0.0)  (1.0,0.0)  (1.0,0.0)  (1.0,0.0) |
     |      .          .          .          .     |
     *                                             *

Plane 1:

B,D                         1
     *                                             *
     |  (1.0,0.0)  (1.0,0.0)  (1.0,0.0)  (1.0,0.0) |
     |  (1.0,0.0)  (1.0,0.0)  (1.0,0.0)  (1.0,0.0) |
 0   |  (1.0,0.0)  (1.0,0.0)  (1.0,0.0)  (1.0,0.0) |
     |  (1.0,0.0)  (1.0,0.0)  (1.0,0.0)  (1.0,0.0) |
     |      .          .          .          .     |
     *                                             *

The following is the 1 × 2 process grid:

B,D  |    0    |  1  
-----| ------- |-----
0    |   P00   |  P01

The following local arrays for X are stored in FFT-packed storage mode:

p,q  |                      0                       |                       1
-----|----------------------------------------------|----------------------------------------------
     |  (1.0,1.0)  (1.0,0.0)  (1.0,1.0)  (1.0,0.0)  |   (1.0,0.0)  (1.0,0.0)  (1.0,0.0)  (1.0,0.0)
     |  (1.0,0.0)  (1.0,0.0)  (1.0,0.0)  (1.0,0.0)  |   (1.0,0.0)  (1.0,0.0)  (1.0,0.0)  (1.0,0.0)
 0   |  (1.0,1.0)  (1.0,0.0)  (1.0,1.0)  (1.0,0.0)  |   (1.0,0.0)  (1.0,0.0)  (1.0,0.0)  (1.0,0.0)
     |  (1.0,0.0)  (1.0,0.0)  (1.0,0.0)  (1.0,0.0)  |   (1.0,0.0)  (1.0,0.0)  (1.0,0.0)  (1.0,0.0)
     |      .          .          .          .      |       .          .          .          .

Output:

Global matrix Y:

          Plane 0:                Plane 1:
----------------------------------------------------
B,D                         0
----------------------------------------------------
     *                                             *
     |  1.0  0.0  0.0  0.0  |   0.0  0.0  0.0  0.0 |
     |  0.0  0.0  0.0  0.0  |   0.0  0.0  0.0  0.0 |
     |  0.0  0.0  0.0  0.0  |   0.0  0.0  0.0  0.0 |
     |  0.0  0.0  0.0  0.0  |   0.0  0.0  0.0  0.0 |
 0   |   .    .    .    .   |    .    .    .    .  |
     |   .    .    .    .   |    .    .    .    .  |
     |   .    .    .    .   |    .    .    .    .  |
     |   .    .    .    .   |    .    .    .    .  |
     |   .    .    .    .   |    .    .    .    .  |
     *                                             *
 
          Plane 2:                Plane 3:
----------------------------------------------------
B,D                         1
----------------------------------------------------
     *                                             *
     |  0.0  0.0  0.0  0.0  |   0.0  0.0  0.0  0.0 |
     |  0.0  0.0  0.0  0.0  |   0.0  0.0  0.0  0.0 |
     |  0.0  0.0  0.0  0.0  |   0.0  0.0  0.0  0.0 |
     |  0.0  0.0  0.0  0.0  |   0.0  0.0  0.0  0.0 |
 0   |   .    .    .    .   |    .    .    .    .  |
     |   .    .    .    .   |    .    .    .    .  |
     |   .    .    .    .   |    .    .    .    .  |
     |   .    .    .    .   |    .    .    .    .  |
     |   .    .    .    .   |    .    .    .    .  |
     *                                             *

The following is the 1 × 2 process grid:

B,D  |    0    |  1  
-----| ------- |-----
0    |   P00   |  P01

Local arrays for Y:

p,q  |                    0                     |                     1
-----|------------------------------------------|------------------------------------------
     |  1.0  0.0  0.0  0.0  0.0  0.0  0.0  0.0  |   0.0  0.0  0.0  0.0  0.0  0.0  0.0  0.0
     |  0.0  0.0  0.0  0.0  0.0  0.0  0.0  0.0  |   0.0  0.0  0.0  0.0  0.0  0.0  0.0  0.0
     |  0.0  0.0  0.0  0.0  0.0  0.0  0.0  0.0  |   0.0  0.0  0.0  0.0  0.0  0.0  0.0  0.0
     |  0.0  0.0  0.0  0.0  0.0  0.0  0.0  0.0  |   0.0  0.0  0.0  0.0  0.0  0.0  0.0  0.0
 0   |   .    .    .    .    .    .    .    .   |    .    .    .    .    .    .    .    .
     |   .    .    .    .    .    .    .    .   |    .    .    .    .    .    .    .    .
     |   .    .    .    .    .    .    .    .   |    .    .    .    .    .    .    .    .
     |   .    .    .    .    .    .    .    .   |    .    .    .    .    .    .    .    .
     |   .    .    .    .    .    .    .    .   |    .    .    .    .    .    .    .    .