Parallel Engineering and Scientific Subroutine Library for AIX Version 2 Release 3: Guide and Reference
This section contains the sample programs and utilities that use the
Fortran 90 and Fortran 77 sparse linear algebraic equations
subroutines. You can use the makefile shown in Makefile to build these sample programs. A copy of
these programs and the makefile are provided with the Parallel ESSL
product. For file names and installation procedures, see the
Parallel ESSL Installation Memo.
The following list describes these sample programs and their
utilities:
- The Fortran 90 and Fortran 77 sample programs shown in Fortran 90 Sample Sparse Program and Fortran 77 Sample Sparse Program, respectively, solve a sparse linear system
based on the discretization of the same elliptic partial differential
equation:
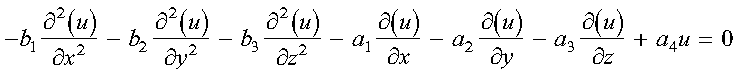
with the Dirichlet boundary conditions on the unit cube, that is,
0 <= x,y,z <= 1. The
equation is discretized with finite differences and uniform stepsize, where
the resulting discrete equation is:
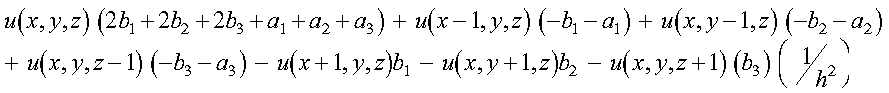
This elliptic partial differential equation is similar to an example
problem discussed in [43].
In these sample programs the index space of the discretized computational
domain is first numbered sequentially in a standard way. Then, the
corresponding vector is distributed using block data distribution, which is
implemented using the subroutine shown in PART_BLOCK (Block Data Distribution).
Boundary conditions are set in a very simple way, by adding equations of
the form:
u(x,y,z) = rhs(x,y,z)
From the command line, you can specify the number of gridpoints along the
edges of the unit cube, the iterative solution method, the preconditioner and
the stopping criterion to be used.
- The Fortran 90 sample program shown in Fortran 90 Sample Sparse Program (using the Harwell-Boeing exchange format) shows how to build and solve a sparse linear system with the
coefficient matrices read from external storage, using the Harwell-Boeing
exchange format. Details on the Harwell-Boeing exchange format and
sample matrices are available from
http://math.nist.gov/MatrixMarket/.
From the command line, you can specify a file containing the input matrix,
an iterative method and preconditioner, and a data distribution to be
used.
This sample program uses the following subroutines:
- Note:
- The performance of the iterative methods depends heavily on the choice of
data distribution. The random data distribution is usually not a good
choice. It is provided to serve as a template to help you implement a
graph partitioning data distribution, which you can do by substituting the
call to the random number generator in the PARTRAND initialization routine
with a call to a graph partitioning package. The data distributions
based on graph partitioning and/or physical considerations usually give the
best performance; in general, experimentation is required to determine
the best data distribution for your particular application.
@process free(f90) init(f90ptr) nosave
!
! This sample program shows how to build and solve a sparse linear
! system using the subroutines in the sparse section of Parallel
! ESSL. The matrix and RHS are generated
! in parallel, so that there is no serial bottleneck.
!
! The program solves a linear system based on the partial differential
! equation
!
!
! b1 dd(u) b2 dd(u) b3 dd(u) a1 d(u) a2 d(u) a3 d(u)
! - ------ - ------ - ------ - ----- - ------ - ------ + a4 u
! dxdx dydy dzdz dx dy dz
!
! = 0
!
! with Dirichlet boundary conditions on the unit cube
!
! 0<=x,y,z<=1
!
! The equation is discretized with finite differences and uniform stepsize;
! the resulting discrete equation is
!
! ( u(x,y,z)(2b1+2b2+2b3+a1+a2+a3)+u(x-1,y,z)(-b1-a1)+u(x,y-1,z)(-b2-a2)+
! + u(x,y,z-1)(-b3-a3)-u(x+1,y,z)b1-u(x,y+1,z)b2-u(x,y,z+1)b3)*(1/h**2)
!
!
! In this sample program the index space of the discretized
! computational domain is first numbered sequentially in a standard way,
! then the corresponding vector is distributed according to an HPF BLOCK
! distribution directive.
!
! Boundary conditions are set in a very simple way, by adding
! equations of the form
!
! u(x,y,z) = rhs(x,y,z)
!
Program PDE90
USE F90SPARSE
Implicit none
INTERFACE PART_BLOCK
! .....user defined subroutine.....
SUBROUTINE PART_BLOCK(GLOBAL_INDX,N,NP,PV,NV)
IMPLICIT NONE
INTEGER, INTENT(IN) :: GLOBAL_INDX, N, NP
INTEGER, INTENT(OUT) :: NV
INTEGER, INTENT(OUT) :: PV(*)
END SUBROUTINE PART_BLOCK
END INTERFACE
! Input parameters
Character*10 :: CMETHD, PREC
Integer :: IDIM, IRET
! Miscellaneous
Integer, Parameter :: IZERO=0, IONE=1
Character, PARAMETER :: ORDER='R'
INTEGER :: IARGC
REAL(KIND(1.D0)), PARAMETER :: DZERO = 0.D0, ONE = 1.D0
REAL(KIND(1.D0)) :: TIMEF, T1, T2, TPREC, TSOLVE, T3, T4
EXTERNAL TIMEF
! Sparse Matrix and preconditioner
TYPE(D_SPMAT) :: A
TYPE(D_PRECN) :: APRC
! Descriptor
TYPE(DESC_TYPE) :: DESC_A
! Dense Matrices
REAL(KIND(1.d0)), POINTER :: B(:), X(:)
! BLACS parameters
INTEGER :: nprow, npcol, icontxt, iam, np, myprow, mypcol
! Solver parameters
INTEGER :: ITER, ITMAX,IERR,ITRACE, METHD,IPREC, ISTOPC,&
& IPARM(20)
REAL(KIND(1.D0)) :: ERR, EPS, RPARM(20)
! Other variables
INTEGER :: I,INFO
INTEGER :: INTERNAL, M,II
! Initialize BLACS
CALL BLACS_PINFO(IAM, NP)
CALL BLACS_GET(IZERO, IZERO, ICONTXT)
! Rectangular Grid, P x 1
CALL BLACS_GRIDINIT(ICONTXT, ORDER, NP, IONE)
CALL BLACS_GRIDINFO(ICONTXT, NPROW, NPCOL, MYPROW, MYPCOL)
!
! Get parameters
!
CALL GET_PARMS(ICONTXT,CMETHD,PREC,IDIM,ISTOPC,ITMAX,ITRACE)
!
! Allocate and fill in the coefficient matrix, RHS and initial guess
!
CALL BLACS_BARRIER(ICONTXT,'All')
T1 = TIMEF()
CALL CREATE_MATRIX(PART_BLOCK,IDIM,A,B,X,DESC_A,ICONTXT)
T2 = TIMEF() - T1
CALL DGAMX2D(ICONTXT,'A',' ',IONE, IONE,T2,IONE,T1,T1,-1,-1,-1)
IF (IAM.EQ.0) Write(6,*) 'Matrix creation Time : ',T2/1.D3
!
! Prepare the preconditioner.
!
SELECT CASE (PREC)
CASE ('ILU')
IPREC = 2
CASE ('DIAGSC')
IPREC = 1
CASE ('NONE')
IPREC = 0
CASE DEFAULT
WRITE(0,*) 'Unknown preconditioner'
CALL BLACS_ABORT(ICONTXT,-1)
END SELECT
CALL BLACS_BARRIER(ICONTXT,'All')
T1 = TIMEF()
CALL PSPGPR(IPREC,A,APRC,DESC_A,INFO=IRET)
TPREC = TIMEF()-T1
CALL DGAMX2D(icontxt,'A',' ',IONE, IONE,TPREC,IONE,t1,t1,-1,-1,-1)
IF (IAM.EQ.0) WRITE(6,*) 'Preconditioner Time : ',TPREC/1.D3
IF (IRET.NE.0) THEN
WRITE(0,*) 'Error on preconditioner',IRET
CALL BLACS_ABORT(ICONTXT,-1)
STOP
END IF
!
! Iterative method parameters
!
IF (CMETHD(1:6).EQ.'CGSTAB') Then
METHD = 1
ELSE IF (CMETHD(1:3).EQ.'CGS') Then
METHD = 2
ELSE IF (CMETHD(1:5).EQ.'TFQMR') THEN
METHD = 3
ELSE
WRITE(0,*) 'Unknown method '
CALL BLACS_ABORT(ICONTXT,-1)
END IF
EPS = 1.D-9
IPARM = 0
RPARM = 0.D0
IPARM(1) = METHD
IPARM(2) = ISTOPC
IPARM(3) = ITMAX
IPARM(4) = ITRACE
RPARM(1) = EPS
CALL BLACS_BARRIER(ICONTXT,'All')
T1 = TIMEF()
CALL PSPGIS(A,B,X,APRC,DESC_A,&
& IPARM=IPARM,RPARM=RPARM,INFO=IERR)
CALL BLACS_BARRIER(ICONTXT,'All')
T2 = TIMEF() - T1
ITER = IPARM(5)
ERR = RPARM(2)
CALL DGAMX2D(ICONTXT,'A',' ',IONE, IONE,T2,IONE,T1,T1,-1,-1,-1)
IF (IAM.EQ.0) THEN
WRITE(6,*) 'Time to Solve Matrix : ',T2/1.D3
WRITE(6,*) 'Time per iteration : ',T2/(ITER*1.D3)
WRITE(6,*) 'Number of iterations : ',ITER
WRITE(6,*) 'Error on exit : ',ERR
WRITE(6,*) 'INFO on exit : ',IERR
END IF
!
! Cleanup storage and exit
!
CALL PGEFREE(B,DESC_A)
CALL PGEFREE(X,DESC_A)
CALL PSPFREE(APRC,DESC_A)
CALL PSPFREE(A,DESC_A)
CALL PADFREE(DESC_A)
CALL BLACS_GRIDEXIT(ICONTXT)
CALL BLACS_EXIT(0)
STOP
CONTAINS
!
! Subroutine to allocate and fill in the coefficient matrix and
! the RHS.
!
SUBROUTINE CREATE_MATRIX(PARTS,IDIM,A,B,T,DESC_A,ICONTXT)
!
! Discretize the partial diferential equation
!
! b1 dd(u) b2 dd(u) b3 dd(u) a1 d(u) a2 d(u) a3 d(u)
! - ------ - ------ - ------ - ----- - ------ - ------ + a4 u
! dxdx dydy dzdz dx dy dz
!
! = 0
!
! boundary condition: Dirichlet
! 0< x,y,z<1
!
! u(x,y,z)(2b1+2b2+2b3+a1+a2+a3)+u(x-1,y,z)(-b1-a1)+u(x,y-1,z)(-b2-a2)+
! + u(x,y,z-1)(-b3-a3)-u(x+1,y,z)b1-u(x,y+1,z)b2-u(x,y,z+1)b3
USE F90SPARSE
Implicit None
INTEGER :: IDIM
INTERFACE PART_BLOCK
SUBROUTINE PARTS(GLOBAL_INDX,N,P,PV,NV)
IMPLICIT NONE
INTEGER, INTENT(IN) :: GLOBAL_INDX, N, P
INTEGER, INTENT(OUT) :: NV
INTEGER, INTENT(OUT) :: PV(*)
END SUBROUTINE PARTS
END INTERFACE
Real(Kind(1.D0)),Pointer :: B(:),T(:)
Type (DESC_TYPE) :: DESC_A
Integer :: ICONTXT
Type(D_SPMAT) :: A
Real(Kind(1.d0)) :: ZT(10),GLOB_X,GLOB_Y,GLOB_Z
Integer :: M,N,NNZ,GLOB_ROW,J
Type (D_SPMAT) :: ROW_MAT
Integer :: X,Y,Z,COUNTER,IA,I,INDX_OWNER
INTEGER :: NPROW,NPCOL,MYPROW,MYPCOL
Integer :: ELEMENT
INTEGER :: INFO, NV, INV
INTEGER, ALLOCATABLE :: PRV(:)
! deltah dimension of each grid cell
! deltat discretization time
Real(Kind(1.D0)) :: DELTAH
Real(Kind(1.d0)),Parameter :: RHS=0.d0,ONE=1.d0,ZERO=0.d0
Real(Kind(1.d0)) :: TIMEF, T1, T2, TINS
external timef
! common area
CALL BLACS_GRIDINFO(ICONTXT, NPROW, NPCOL, MYPROW, MYPCOL)
DELTAH = 1.D0/(IDIM-1)
! Initialize array descriptor and sparse matrix storage. Provide an
! estimate of the number of non zeroes
M = IDIM*IDIM*IDIM
N = M
NNZ = (N*7)/(NPROW*NPCOL)
Call PADALL(N,PARTS,DESC_A,ICONTXT)
Call PSPALL(A,DESC_A,NNZ=NNZ)
! Define RHS from boundary conditions; also build initial guess
Call PGEALL(B,DESC_A)
Call PGEALL(T,DESC_A)
! We build an auxiliary matrix consisting of one row at a
! time
ROW_MAT%DESCRA(1:1) = 'G'
ROW_MAT%FIDA = 'CSR'
ALLOCATE(ROW_MAT%AS(20))
ALLOCATE(ROW_MAT%IA1(20))
ALLOCATE(ROW_MAT%IA2(20))
ALLOCATE(PRV(NPROW))
ROW_MAT%IA2(1)=1
TINS = 0.D0
CALL BLACS_BARRIER(ICONTXT,'ALL')
T1 = TIMEF()
! Loop over rows belonging to current process in a BLOCK
! distribution.
DO GLOB_ROW = 1, N
CALL PARTS(GLOB_ROW,N,NPROW,PRV,NV)
DO INV = 1, NV
INDX_OWNER = PRV(INV)
IF (INDX_OWNER == MYPROW) THEN
! Local matrix pointer
ELEMENT=1
! Compute gridpoint Coordinates
IF (MOD(GLOB_ROW,(IDIM*IDIM)).EQ.0) THEN
X = GLOB_ROW/(IDIM*IDIM)
ELSE
X = GLOB_ROW/(IDIM*IDIM)+1
ENDIF
IF (MOD((GLOB_ROW-(X-1)*IDIM*IDIM),IDIM).EQ.0) THEN
Y = (GLOB_ROW-(X-1)*IDIM*IDIM)/IDIM
ELSE
Y = (GLOB_ROW-(X-1)*IDIM*IDIM)/IDIM+1
ENDIF
Z = GLOB_ROW-(X-1)*IDIM*IDIM-(Y-1)*IDIM
! GLOB_X, GLOB_Y, GLOB_X coordinates
GLOB_X=X*DELTAH
GLOB_Y=Y*DELTAH
GLOB_Z=Z*DELTAH
! Check on boundary points
IF (X.EQ.1) THEN
ROW_MAT%AS(ELEMENT)=ONE
ROW_MAT%IA1(ELEMENT)=(X-1)*IDIM*IDIM+(Y-1)*IDIM+(Z)
ELEMENT=ELEMENT+1
ELSE IF (Y.EQ.1) THEN
ROW_MAT%AS(ELEMENT)=ONE
ROW_MAT%IA1(ELEMENT)=(X-1)*IDIM*IDIM+(Y-1)*IDIM+(Z)
ELEMENT=ELEMENT+1
ELSE IF (Z.EQ.1) THEN
ROW_MAT%AS(ELEMENT)=ONE
ROW_MAT%IA1(ELEMENT)=(X-1)*IDIM*IDIM+(Y-1)*IDIM+(Z)
ELEMENT=ELEMENT+1
ELSE IF (X.EQ.IDIM) THEN
ROW_MAT%AS(ELEMENT)=ONE
ROW_MAT%IA1(ELEMENT)=(X-1)*IDIM*IDIM+(Y-1)*IDIM+(Z)
ELEMENT=ELEMENT+1
ELSE IF (Y.EQ.IDIM) THEN
ROW_MAT%AS(ELEMENT)=ONE
ROW_MAT%IA1(ELEMENT)=(X-1)*IDIM*IDIM+(Y-1)*IDIM+(Z)
ELEMENT=ELEMENT+1
ELSE IF (Z.EQ.IDIM) THEN
ROW_MAT%AS(ELEMENT)=ONE
ROW_MAT%IA1(ELEMENT)=(X-1)*IDIM*IDIM+(Y-1)*IDIM+(Z)
ELEMENT=ELEMENT+1
ELSE
! Internal point: build discretization
!
! Term depending on (x-1,y,z)
!
ROW_MAT%AS(ELEMENT)=-B1(GLOB_X,GLOB_Y,GLOB_Z)&
& -A1(GLOB_X,GLOB_Y,GLOB_Z)
ROW_MAT%AS(ELEMENT) = ROW_MAT%AS(ELEMENT)/(DELTAH*&
& DELTAH)
ROW_MAT%IA1(ELEMENT)=(X-2)*IDIM*IDIM+(Y-1)*IDIM+(Z)
ELEMENT=ELEMENT+1
! Term depending on (x,y-1,z)
ROW_MAT%AS(ELEMENT)=-B2(GLOB_X,GLOB_Y,GLOB_Z)&
& -A2(GLOB_X,GLOB_Y,GLOB_Z)
ROW_MAT%AS(ELEMENT) = ROW_MAT%AS(ELEMENT)/(DELTAH*&
& DELTAH)
ROW_MAT%IA1(ELEMENT)=(X-1)*IDIM*IDIM+(Y-2)*IDIM+(Z)
ELEMENT=ELEMENT+1
! Term depending on (x,y,z-1)
ROW_MAT%AS(ELEMENT)=-B3(GLOB_X,GLOB_Y,GLOB_Z)&
& -A3(GLOB_X,GLOB_Y,GLOB_Z)
ROW_MAT%AS(ELEMENT) = ROW_MAT%AS(ELEMENT)/(DELTAH*&
& DELTAH)
ROW_MAT%IA1(ELEMENT)=(X-1)*IDIM*IDIM+(Y-1)*IDIM+(Z-1)
ELEMENT=ELEMENT+1
! Term depending on (x,y,z)
ROW_MAT%AS(ELEMENT)=2*B1(GLOB_X,GLOB_Y,GLOB_Z)&
& +2*B2(GLOB_X,GLOB_Y,GLOB_Z)&
& +2*B3(GLOB_X,GLOB_Y,GLOB_Z)&
& +A1(GLOB_X,GLOB_Y,GLOB_Z)&
& +A2(GLOB_X,GLOB_Y,GLOB_Z)&
& +A3(GLOB_X,GLOB_Y,GLOB_Z)
ROW_MAT%AS(ELEMENT) = ROW_MAT%AS(ELEMENT)/(DELTAH*&
& DELTAH)
ROW_MAT%IA1(ELEMENT)=(X-1)*IDIM*IDIM+(Y-1)*IDIM+(Z)
ELEMENT=ELEMENT+1
! Term depending on (x,y,z+1)
ROW_MAT%AS(ELEMENT)=-B1(GLOB_X,GLOB_Y,GLOB_Z)
ROW_MAT%AS(ELEMENT) = ROW_MAT%AS(ELEMENT)/(DELTAH*&
& DELTAH)
ROW_MAT%IA1(ELEMENT)=(X-1)*IDIM*IDIM+(Y-1)*IDIM+(Z+1)
ELEMENT=ELEMENT+1
! Term depending on (x,y+1,z)
ROW_MAT%AS(ELEMENT)=-B2(GLOB_X,GLOB_Y,GLOB_Z)
ROW_MAT%AS(ELEMENT) = ROW_MAT%AS(ELEMENT)/(DELTAH*&
& DELTAH)
ROW_MAT%IA1(ELEMENT)=(X-1)*IDIM*IDIM+(Y)*IDIM+(Z)
ELEMENT=ELEMENT+1
! Term depending on (x+1,y,z)
ROW_MAT%AS(ELEMENT)=-B3(GLOB_X,GLOB_Y,GLOB_Z)
ROW_MAT%AS(ELEMENT) = ROW_MAT%AS(ELEMENT)/(DELTAH*&
& DELTAH)
ROW_MAT%IA1(ELEMENT)=(X)*IDIM*IDIM+(Y-1)*IDIM+(Z)
ELEMENT=ELEMENT+1
ENDIF
ROW_MAT%M=1
ROW_MAT%N=N
ROW_MAT%IA2(2)=ELEMENT
! IA== GLOBAL ROW INDEX
IA=(X-1)*IDIM*IDIM+(Y-1)*IDIM+(Z)
T3 = TIMEF()
CALL PSPINS(A,IA,1,ROW_MAT,DESC_A)
TINS = TINS + (TIMEF()-T3)
! Build RHS
IF (X==1) THEN
GLOB_Y=(Y-IDIM/2)*DELTAH
GLOB_Z=(Z-IDIM/2)*DELTAH
ZT(1) = EXP(-GLOB_Y**2-GLOB_Z**2)
ELSE IF ((Y==1).OR.(Y==IDIM).OR.(Z==1).OR.(Z==IDIM)) THEN
GLOB_X=3*(X-1)*DELTAH
GLOB_Y=(Y-IDIM/2)*DELTAH
GLOB_Z=(Z-IDIM/2)*DELTAH
ZT(1) = EXP(-GLOB_Y**2-GLOB_Z**2)*EXP(-GLOB_X)
ELSE
ZT(1) = 0.D0
ENDIF
CALL PGEINS(B,ZT(1:1),DESC_A,IA)
ZT(1)=0.D0
CALL PGEINS(T,ZT(1:1),DESC_A,IA)
END IF
END DO
END DO
CALL BLACS_BARRIER(ICONTXT,'ALL')
T2 = TIMEF()
IF (MYPROW.EQ.0) THEN
WRITE(0,*) ' pspins time',TINS/1.D3
WRITE(0,*) ' Insert time',(T2-T1)/1.D3
ENDIF
DEALLOCATE(ROW_MAT%AS,ROW_MAT%IA1,ROW_MAT%IA2)
CALL BLACS_BARRIER(ICONTXT,'ALL')
T1 = TIMEF()
CALL PSPASB(A,DESC_A,INFO=INFO,DUPFLAG=0,MTYPE='GEN ')
CALL BLACS_BARRIER(ICONTXT,'ALL')
T2 = TIMEF()
IF (MYPROW.EQ.0) THEN
WRITE(0,*) ' Assembly time',(T2-T1)/1.D3
ENDIF
CALL PGEASB(B,DESC_A)
CALL PGEASB(T,DESC_A)
RETURN
END SUBROUTINE CREATE_MATRIX
!
! Functions parameterizing the differential equation
!
FUNCTION A1(X,Y,Z)
REAL(KIND(1.D0)) :: A1
REAL(KIND(1.D0)) :: X,Y,Z
A1=1.D0
END FUNCTION A1
FUNCTION A2(X,Y,Z)
REAL(KIND(1.D0)) :: A2
REAL(KIND(1.D0)) :: X,Y,Z
A2=2.D1*Y
END FUNCTION A2
FUNCTION A3(X,Y,Z)
REAL(KIND(1.D0)) :: A3
REAL(KIND(1.D0)) :: X,Y,Z
A3=1.D0
END FUNCTION A3
FUNCTION A4(X,Y,Z)
REAL(KIND(1.D0)) :: A4
REAL(KIND(1.D0)) :: X,Y,Z
A4=1.D0
END FUNCTION A4
FUNCTION B1(X,Y,Z)
REAL(KIND(1.D0)) :: B1
REAL(KIND(1.D0)) :: X,Y,Z
B1=1.D0
END FUNCTION B1
FUNCTION B2(X,Y,Z)
REAL(KIND(1.D0)) :: B2
REAL(KIND(1.D0)) :: X,Y,Z
B2=1.D0
END FUNCTION B2
FUNCTION B3(X,Y,Z)
REAL(KIND(1.D0)) :: B3
REAL(KIND(1.D0)) :: X,Y,Z
B3=1.D0
END FUNCTION B3
!
! Get iteration parameters from the command line
!
SUBROUTINE GET_PARMS(ICONTXT,CMETHD,PREC,IDIM,ISTOPC,ITMAX,ITRACE)
integer :: icontxt
Character*10 :: CMETHD, PREC
Integer :: IDIM, IRET, ISTOPC,ITMAX,ITRACE
Character*40 :: CHARBUF
INTEGER :: IARGC, NPROW, NPCOL, MYPROW, MYPCOL
EXTERNAL IARGC
INTEGER :: INTBUF(10), IP
CALL BLACS_GRIDINFO(ICONTXT, NPROW, NPCOL, MYPROW, MYPCOL)
IF (MYPROW==0) THEN
! Read command line parameters
IP=IARGC()
IF (IARGC().GE.3) THEN
CALL GETARG(1,CHARBUF)
READ(CHARBUF,*) CMETHD
CALL GETARG(2,CHARBUF)
READ(CHARBUF,*) PREC
! Convert strings in array
DO I = 1, LEN(CMETHD)
INTBUF(I) = IACHAR(CMETHD(I:I))
END DO
! Broadcast parameters to all processors
CALL IGEBS2D(ICONTXT,'ALL',' ',10,1,INTBUF,10)
DO I = 1, LEN(PREC)
INTBUF(I) = IACHAR(PREC(I:I))
END DO
! Broadcast parameters to all processors
CALL IGEBS2D(ICONTXT,'ALL',' ',10,1,INTBUF,10)
CALL GETARG(3,CHARBUF)
READ(CHARBUF,*) IDIM
IF (IARGC().GE.4) THEN
CALL GETARG(4,CHARBUF)
READ(CHARBUF,*) ISTOPC
ELSE
ISTOPC=1
ENDIF
IF (IARGC().GE.5) THEN
CALL GETARG(5,CHARBUF)
READ(CHARBUF,*) ITMAX
ELSE
ITMAX=500
ENDIF
IF (IARGC().GE.6) THEN
CALL GETARG(6,CHARBUF)
READ(CHARBUF,*) ITRACE
ELSE
ITRACE=0
ENDIF
! Broadcast parameters to all processors
CALL IGEBS2D(ICONTXT,'ALL',' ',1,1,IDIM,1)
CALL IGEBS2D(ICONTXT,'ALL',' ',1,1,ISTOPC,1)
CALL IGEBS2D(ICONTXT,'ALL',' ',1,1,ITMAX,1)
CALL IGEBS2D(ICONTXT,'ALL',' ',1,1,ITRACE,1)
WRITE(6,*)'Solving matrix: ELL1'
WRITE(6,*)'on grid',IDIM,'x',IDIM,'x',IDIM
WRITE(6,*)' with BLOCK data distribution, NP=',Np,&
& ' Preconditioner=',PREC,&
& ' Iterative methd=',CMETHD
ELSE
! Wrong number of parameter, print an error message and exit
CALL PR_USAGE(0)
CALL BLACS_ABORT(ICONTXT,-1)
STOP 1
ENDIF
ELSE
! Receive Parameters
CALL IGEBR2D(ICONTXT,'ALL',' ',10,1,INTBUF,10,0,0)
DO I = 1, 10
CMETHD(I:I) = ACHAR(INTBUF(I))
END DO
CALL IGEBR2D(ICONTXT,'ALL',' ',10,1,INTBUF,10,0,0)
DO I = 1, 10
PREC(I:I) = ACHAR(INTBUF(I))
END DO
CALL IGEBR2D(ICONTXT,'ALL',' ',1,1,IDIM,1,0,0)
CALL IGEBR2D(ICONTXT,'ALL',' ',1,1,ISTOPC,1,0,0)
CALL IGEBR2D(ICONTXT,'ALL',' ',1,1,ITMAX,1,0,0)
CALL IGEBR2D(ICONTXT,'ALL',' ',1,1,ITRACE,1,0,0)
END IF
RETURN
END SUBROUTINE GET_PARMS
!
! Print an error message
!
SUBROUTINE PR_USAGE(IOUT)
INTEGER :: IOUT
WRITE(IOUT,*)'Incorrect parameter(s) found'
WRITE(IOUT,*)' Usage: pde90 methd prec dim &
&[istop itmax itrace]'
WRITE(IOUT,*)' Where:'
WRITE(IOUT,*)' methd: CGSTAB TFQMR CGS'
WRITE(IOUT,*)' prec : ILU DIAGSC NONE'
WRITE(IOUT,*)' dim number of points along each axis'
WRITE(IOUT,*)' the size of the resulting linear '
WRITE(IOUT,*)' system is dim**3'
WRITE(IOUT,*)' istop Stopping criterion 1, 2 or 3 [1] '
WRITE(IOUT,*)' itmax Maximum number of iterations [500] '
WRITE(IOUT,*)' itrace 0 (no tracing, default) or '
WRITE(IOUT,*)' >= 0 do tracing every ITRACE'
WRITE(IOUT,*)' iterations '
END SUBROUTINE PR_USAGE
END PROGRAM PDE90
C
C This sample program shows how to build and solve a sparse linear
C system using the subroutines in the sparse section of Parallel
C ESSL. The matrix and RHS are generated
C in parallel, so that there is no serial bottleneck.
C
C The program solves a linear system based on the partial differential equation
C
C b1 dd(u) b2 dd(u) b3 dd(u) a1 d(u) a2 d(u) a3 d(u)
C - ------ - ------ - ------ - ----- - ------ - ------ + a4 u
C dxdx dydy dzdz dx dy dz
C
C = 0
C
C with Dirichlet boundary conditions on the unit cube
C
C 0<=x,y,z<=1
C
C The equation is discretized with finite differences and uniform stepsize;
C the resulting discrete equation is
C
C ( u(x,y,z)(2b1+2b2+2b3+a1+a2+a3)+u(x-1,y,z)(-b1-a1)+u(x,y-1,z)(-b2-a2)+
C + u(x,y,z-1)(-b3-a3)-u(x+1,y,z)b1-u(x,y+1,z)b2-u(x,y,z+1)b3)*(1/h**2)
C
C
C In this sample program the index space of the discretized
C computational domain is first numbered sequentially in a standard way,
C then the corresponding vector is distributed according to an HPF BLOCK
C distribution directive.
C
C Boundary conditions are set in a very simple way, by adding
C equations of the form
C
C u(x,y,z) = rhs(x,y,z)
C
C
Program PDE77
USE F90SPARSE
Implicit none
EXTERNAL PART_BLOCK
C Input parameters
Character*10 :: CMETHD, PREC
Integer :: IDIM
C Miscellaneous
Integer, Parameter :: IZERO=0, IONE=1
Character, PARAMETER :: ORDER='R'
REAL(KIND(1.D0)), POINTER :: B_COL(:), X_COL(:)
INTEGER :: NR, NNZ,IRCODE, NNZ1, NRHS
REAL(KIND(1.D0)), PARAMETER :: DZERO = 0.D0, ONE = 1.D0
REAL(KIND(1.D0)) :: TIMEF, T1, T2, TPREC, TSOLVE, T3, T4
REAL(KIND(1.D0)), POINTER :: DWORK(:)
EXTERNAL TIMEF
LOGICAL, PARAMETER :: UPDATE=.TRUE., NOUPDATE=.FALSE.
C Sparse Matrices
REAL(8), POINTER :: AS(:), PRCS(:)
INTEGER, POINTER :: DESC_A(:), IA1(:), IA2(:)
INTEGER :: INFOA(30)
C Dense Matrices
REAL(KIND(1.D0)), POINTER :: B(:), X(:)
INTEGER :: LB, LX, LDV, LDV1,IRET
INTERFACE
SUBROUTINE CREATE_MTRX_ELL1_BLOCK(PARTS,IDIM,
+ AS,IA1,IA2,INFOA,B,T,DESC_A,ICONTXT)
Implicit None
external parts
Integer :: IDIM
Real(Kind(1.D0)),Pointer :: B(:), T(:), AS(:)
integer :: infoa(30)
INTEGER, POINTER :: DESC_A(:), IA1(:),IA2(:)
Integer :: ICONTXT
end SUBROUTINE CREATE_MTRX_ELL1_BLOCK
END INTERFACE
C Communications data structure
C BLACS parameters
INTEGER :: nprow, npcol, icontxt, iam, np, myprow,
+ mypcol
C Solver parameters
Integer :: iter, itmax,ierr,itrace, methd,iprec,
+ istopc, iparm(20)
real(kind(1.d0)) :: err, eps, rparm(20)
C Other variables
Integer :: i,info
INTEGER :: INTERNAL, M,ii,nnzero
C Initialize BLACS
CALL BLACS_PINFO(IAM, NP)
CALL BLACS_GET(IZERO, IZERO, ICONTXT)
C Rectangular Grid, Np x 1
CALL BLACS_GRIDINIT(ICONTXT, ORDER, NP, IONE)
CALL BLACS_GRIDINFO(ICONTXT, NPROW, NPCOL, MYPROW, MYPCOL)
C
C Get parameters
C
CALL GET_PARMS(ICONTXT,CMETHD,PREC,IDIM,ISTOPC,ITMAX,ITRACE)
C
C Allocate and fill in the coefficient matrix and the RHS
C
CALL BLACS_BARRIER(ICONTXT,'All')
T1 = TIMEF()
CALL CREATE_MTRX_ELL1_BLOCK(PART_BLOCK,IDIM,
+ AS,IA1,IA2,INFOA,B,X,DESC_A,ICONTXT)
T2 = TIMEF() - T1
CALL DGAMX2D(ICONTXT,'A',' ',IONE, IONE,T2,IONE,T1,T1,-1,-1,-1)
IF (IAM.EQ.0) Write(6,*) 'Matrix creation Time : ',T2/1.D3
LB = SIZE(B)
LX = SIZE(X)
LDV = DESC_A(5)
LDV1 = DESC_A(6)
NNZ = SIZE(AS)
NNZ1 = SIZE(IA1)
ALLOCATE(PRCS(2*NNZ+LDV+LDV1+31),STAT=IRCODE)
IF (IRCODE /= 0) THEN
WRITE(0,*) 'Allocation error'
CALL BLACS_ABORT(ICONTXT,-1)
STOP
ENDIF
C
C Prepare the preconditioning data structure
C
SELECT CASE (PREC)
CASE ('ILU')
IPREC = 2
CASE ('DIAGSC')
IPREC = 1
CASE ('NONE')
IPREC = 0
CASE DEFAULT
WRITE(0,*) 'Unknown preconditioner'
CALL BLACS_ABORT(ICONTXT,-1)
END SELECT
CALL BLACS_BARRIER(ICONTXT,'All')
T1 = TIMEF()
CALL PDSPGPR(IPREC,AS,IA1,IA2,INFOA,PRCS,SIZE(PRCS),DESC_A,IRET)
TPREC = TIMEF()-T1
CALL DGAMX2D(icontxt,'A',' ',IONE, IONE,TPREC,IONE,t1,t1,-1,-1,-1)
IF (IAM.EQ.0) WRITE(6,*) 'Preconditioner Time : ',TPREC/1.D3
if (iret.ne.0) then
write(0,*) 'Error on preconditioner',iret
call blacs_abort(icontxt,-1)
stop
endif
C
C Iteration parameters
C
IF (CMETHD(1:6).EQ.'CGSTAB') Then
METHD = 1
ELSE IF (CMETHD(1:3).EQ.'CGS') Then
METHD = 2
ELSE IF (CMETHD(1:5).EQ.'TFQMR') THEN
METHD = 3
ELSE
WRITE(0,*) 'Unknown method '
CALL BLACS_ABORT(ICONTXT,-1)
END IF
EPS = 1.D-9
IPARM = 0
RPARM = 0.D0
IPARM(1) = METHD
IPARM(2) = ISTOPC
IPARM(3) = ITMAX
IPARM(4) = ITRACE
RPARM(1) = EPS
NRHS = 1
CALL BLACS_BARRIER(ICONTXT,'All')
T1 = TIMEF()
CALL PDSPGIS(AS,IA1,IA2,INFOA,NRHS,B,LB,X,LX,PRCS,
+ DESC_A,IPARM,RPARM,INFO)
CALL BLACS_BARRIER(ICONTXT,'All')
TSOLVE = TIMEF() - T1
ERR = RPARM(2)
ITER = IPARM(5)
IF (IAM.EQ.0) THEN
WRITE(6,*) 'Time to Solve Matrix : ',TSOLVE/1.D3
WRITE(6,*) 'Time per iteration : ',TSOLVE/(1.D3*ITER)
WRITE(6,*) 'Number of iterations : ',ITER
WRITE(6,*) 'Error on exit : ',ERR
WRITE(6,*) 'INFO on exit:',INFO
END IF
CALL BLACS_GRIDEXIT(ICONTXT)
CALL BLACS_EXIT(0)
STOP
END
C
C Print an error message
C
SUBROUTINE PR_USAGE(IOUT)
INTEGER :: IOUT
WRITE(IOUT,*)'Incorrect parameter(s) found'
WRITE(IOUT,*)
+ ' Usage: pde77 methd prec dim [istopc itmax itrace]'
WRITE(IOUT,*)' Where:'
WRITE(IOUT,*)' methd: CGSTAB TFQMR CGS'
WRITE(IOUT,*)' prec : ILU DIAGSC NONE'
WRITE(IOUT,*)' dim number of points along each axis'
WRITE(IOUT,*)' the size of the resulting linear '
WRITE(IOUT,*)' system is dim**3'
WRITE(IOUT,*)' istopc Stopping criterion 1 2 or 3 [1] '
WRITE(IOUT,*)' itmax Maximum number of iterations [500]'
WRITE(IOUT,*)' itrace 0 (no tracing, default) or '
WRITE(IOUT,*)' >= 0 do tracing every ITRACE'
WRITE(IOUT,*)' iterations '
RETURN
END
C
C Functions parameterizing the differential equation
C
FUNCTION A1(X,Y,Z)
REAL(KIND(1.D0)) :: A1
REAL(KIND(1.D0)) :: X,Y,Z
A1=1.D0
END
FUNCTION A2(X,Y,Z)
REAL(KIND(1.D0)) :: A2
REAL(KIND(1.D0)) :: X,Y,Z
A2=2.D1*Y
END
FUNCTION A3(X,Y,Z)
REAL(KIND(1.D0)) :: A3
REAL(KIND(1.D0)) :: X,Y,Z
A3=1.D0
END
FUNCTION A4(X,Y,Z)
REAL(KIND(1.D0)) :: A4
REAL(KIND(1.D0)) :: X,Y,Z
A4=1.D0
END
FUNCTION B1(X,Y,Z)
REAL(KIND(1.D0)) :: B1
REAL(KIND(1.D0)) :: X,Y,Z
B1=1.D0
END
FUNCTION B2(X,Y,Z)
REAL(KIND(1.D0)) :: B2
REAL(KIND(1.D0)) :: X,Y,Z
B2=1.D0
END
FUNCTION B3(X,Y,Z)
REAL(KIND(1.D0)) :: B3
REAL(KIND(1.D0)) :: X,Y,Z
B3=1.D0
END
C
C Subroutine to allocate and fill in the coefficient matrix and
C the RHS.
C
SUBROUTINE CREATE_MTRX_ELL1_BLOCK(PARTS,IDIM,
+ AS,IA1,IA2,INFOA,B,T,DESC_A,ICONTXT)
C
C the equation generated is:
C b1 d d (u) b2 d d (u) b3 d d (u) a1 d (u)) a2 d (u))) a3d (u)) a4 u
C - ------ - ------ - ------ - ----- - ------ - ------ +
C dx dx dy dy dz dz dx dy dz
C
C =g(x,y,z)
C where g is the RHS extracted from exact solution:
C f(x,y,z)=10.d0*X*Y*Z*(1-X)*(1-Y)*(1-Z)*EXP(X**4.5)
C boundary condition: Dirichlet
C 0< x,y,z<1
C discretized with finite differences; the discrete equation is
C u(x,y,z)(2b1+2b2+2b3+a1+a2+a3)+u(x-1,y,z)(-b1-a1)+u(x,y-1,z)(-b2-a2)+
C + u(x,y,z-1)(-b3-a3)-u(x+1,y,z)b1-u(x,y+1,z)b2-u(x,y,z+1)b3
C !!this matrix is non symmetric
USE F90SPARSE
EXTERNAL PARTS
Implicit None
Integer :: IDIM
Real(Kind(1.D0)),Pointer :: B(:), T(:), AS(:)
integer :: infoa(20)
INTEGER, POINTER :: DESC_A(:), IA1(:),IA2(:)
Integer :: ICONTXT
Real(Kind(1.d0)) :: ZT(10),GLOB_X,GLOB_Y,GLOB_Z,
+ ras(20)
Integer :: M,N,NNZ,glob_row,nr,j
integer :: ria1(20),ria2(20),rinfoa(30)
Real(Kind(1.D0)),POINTER :: SOL(:)
real(kind(1.d0)), external :: a1,a2,a3,b1,b2,b3
Integer :: X,Y,Z,COUNTER,IA,I,NPROW,NPCOL,MYPROW
+ ,MYPCOL,DOMAIN_INDEX
Integer :: BOUND_COND_0YZ, BOUND_COND_1YZ,
+ BOUND_COND_X0Z , BOUND_COND_X1Z , BOUND_COND_XY0 ,
+ BOUND_COND_XY1,MP,ELEMENT,LDSCA,IRCODE, NNZ1
REAL(KIND(1.D0)) :: DELTAH
INTEGER :: GAP,INFO
integer :: prv(64), indx_owner, nv,inv
C deltah dimension of each grid cell
C deltat discretization time
Real(Kind(1.d0)),Parameter :: RHS=0.d0,ONE=1.d0,ZERO=0.d0
Real(Kind(1.d0)) :: TIMEF, T1, T2,t3, TINS
external timef
C common area
INTEGER DIM_BLOCK, NPROC
CALL BLACS_GRIDINFO(ICONTXT, NPROW, NPCOL, MYPROW, MYPCOL)
NPROC = NPROW*NPCOL
DELTAH=1.D0/(IDIM-1)
M = IDIM*IDIM*IDIM
N = M
LDSCA = 3*N+31+3*NPROC
DIM_BLOCK=(N+NPROC-1)/NPROC
NNZ = MAX(2,(N*7)/(NPROC))
NNZ1 = MAX(2,(N*9)/(NPROC))+MAX(1,DIM_BLOCK)
ALLOCATE(DESC_A(LDSCA),AS(NNZ),IA1(NNZ1),
+ IA2(NNZ1),STAT=IRCODE)
IF (IRCODE /= 0) THEN
WRITE(0,*) 'Allocation error in CREATE'
CALL BLACS_ABORT(ICONTXT,-1)
STOP
ENDIF
INFOA(1) = NNZ
INFOA(2) = NNZ1
INFOA(3) = NNZ1
DESC_A(11) = LDSCA
CALL PADINIT(N,PARTS,DESC_A,ICONTXT)
NR = DESC_A(5)
ALLOCATE(B(NR),T(NR),STAT=IRCODE)
IF (IRCODE /= 0) THEN
WRITE(0,*) 'Allocation error in CREATE'
CALL BLACS_ABORT(ICONTXT,-1)
STOP
ENDIF
CALL PDSPINIT(AS,IA1,IA2,INFOA,DESC_A)
C
C We build an auxiliary matrix consisting of one row at a
C time in CSR mode
C
RINFOA(4) = 1
RINFOA(5) = 1
RINFOA(6) = 1
RINFOA(7) = N
GAP = 1
RIA2(1)=1
TINS = 0.D0
CALL BLACS_BARRIER(ICONTXT,'ALL')
T1 = TIMEF()
C Loop over all rows which belongs to me; we have a BLOCK
C distribution !!
DO GLOB_ROW = 1, N
CALL PARTS(GLOB_ROW,N,NPROW,PRV,NV)
DO INV = 1, NV
INDX_OWNER = PRV(INV)
IF (INDX_OWNER == MYPROW) THEN
ELEMENT=1
C GLOB_X, GLOB_Y, GLOB_X coordinates in current measure unit
C Compute Point Coordinates
IF (MOD(GLOB_ROW,(IDIM*IDIM)).EQ.0) THEN
X = GLOB_ROW/(IDIM*IDIM)
ELSE
X = GLOB_ROW/(IDIM*IDIM)+1
ENDIF
IF (MOD((GLOB_ROW-(X-1)*IDIM*IDIM),IDIM).EQ.0) THEN
Y = (GLOB_ROW-(X-1)*IDIM*IDIM)/IDIM
ELSE
Y = (GLOB_ROW-(X-1)*IDIM*IDIM)/IDIM+1
ENDIF
Z = GLOB_ROW-(X-1)*IDIM*IDIM-(Y-1)*IDIM
GLOB_X=X*DELTAH
GLOB_Y=Y*DELTAH
GLOB_Z=Z*DELTAH
IF (X.EQ.1) THEN
RAS(ELEMENT)=ONE
RIA1(ELEMENT)=(X-1)*IDIM*IDIM+(Y-1)*IDIM+(Z)
ELEMENT=ELEMENT+1
ELSE IF (Y.EQ.1) THEN
RAS(ELEMENT)=ONE
RIA1(ELEMENT)=(X-1)*IDIM*IDIM+(Y-1)*IDIM+(Z)
ELEMENT=ELEMENT+1
ELSE IF (Z.EQ.1) THEN
RAS(ELEMENT)=ONE
RIA1(ELEMENT)=(X-1)*IDIM*IDIM+(Y-1)*IDIM+(Z)
ELEMENT=ELEMENT+1
ELSE IF (X.EQ.IDIM) THEN
RAS(ELEMENT)=ONE
RIA1(ELEMENT)=(X-1)*IDIM*IDIM+(Y-1)*IDIM+(Z)
ELEMENT=ELEMENT+1
ELSE IF (Y.EQ.IDIM) THEN
RAS(ELEMENT)=ONE
RIA1(ELEMENT)=(X-1)*IDIM*IDIM+(Y-1)*IDIM+(Z)
ELEMENT=ELEMENT+1
ELSE IF (Z.EQ.IDIM) THEN
RAS(ELEMENT)=ONE
RIA1(ELEMENT)=(X-1)*IDIM*IDIM+(Y-1)*IDIM+(Z)
ELEMENT=ELEMENT+1
ELSE
C ! .....internal point......
C ! (x-1,y,z)
RAS(ELEMENT)=-B1(GLOB_X,GLOB_Y,GLOB_Z)
+ -A1(GLOB_X,GLOB_Y,GLOB_Z)
RAS(ELEMENT) = RAS(ELEMENT)/(DELTAH*DELTAH)
RIA1(ELEMENT)=(X-2)*IDIM*IDIM+(Y-1)*IDIM+(Z)
ELEMENT=ELEMENT+1
C ! (x,y-1,z)
RAS(ELEMENT)=-B2(GLOB_X,GLOB_Y,GLOB_Z)
+ -A2(GLOB_X,GLOB_Y,GLOB_Z)
RAS(ELEMENT) = RAS(ELEMENT)/(DELTAH*DELTAH)
RIA1(ELEMENT)=(X-1)*IDIM*IDIM+(Y-2)*IDIM+(Z)
ELEMENT=ELEMENT+1
C ! (x,y,z-1)
RAS(ELEMENT)=-B3(GLOB_X,GLOB_Y,GLOB_Z)
+ -A3(GLOB_X,GLOB_Y,GLOB_Z)
RAS(ELEMENT) = RAS(ELEMENT)/(DELTAH*DELTAH)
RIA1(ELEMENT)=(X-1)*IDIM*IDIM+(Y-1)*IDIM+(Z-1)
ELEMENT=ELEMENT+1
C ! (x,y,z)
RAS(ELEMENT)=2*B1(GLOB_X,GLOB_Y,GLOB_Z)
+ +2*B2(GLOB_X,GLOB_Y,GLOB_Z)
+ +2*B3(GLOB_X,GLOB_Y,GLOB_Z)
+ +A1(GLOB_X,GLOB_Y,GLOB_Z)
+ +A2(GLOB_X,GLOB_Y,GLOB_Z)
+ +A3(GLOB_X,GLOB_Y,GLOB_Z)
RAS(ELEMENT) = RAS(ELEMENT)/(DELTAH*DELTAH)
RIA1(ELEMENT)=(X-1)*IDIM*IDIM+(Y-1)*IDIM+(Z)
ELEMENT=ELEMENT+1
C ! (x,y,z+1)
RAS(ELEMENT)=-B1(GLOB_X,GLOB_Y,GLOB_Z)
RAS(ELEMENT) = RAS(ELEMENT)/(DELTAH*DELTAH)
RIA1(ELEMENT)=(X-1)*IDIM*IDIM+(Y-1)*IDIM+(Z+1)
ELEMENT=ELEMENT+1
C ! (x,y+1,z)
RAS(ELEMENT)=-B2(GLOB_X,GLOB_Y,GLOB_Z)
RAS(ELEMENT) = RAS(ELEMENT)/(DELTAH*DELTAH)
RIA1(ELEMENT)=(X-1)*IDIM*IDIM+(Y)*IDIM+(Z)
ELEMENT=ELEMENT+1
C ! (x+1,y,z)
RAS(ELEMENT)=-B3(GLOB_X,GLOB_Y,GLOB_Z)
RAS(ELEMENT) = RAS(ELEMENT)/(DELTAH*DELTAH)
RIA1(ELEMENT)=(X)*IDIM*IDIM+(Y-1)*IDIM+(Z)
ELEMENT=ELEMENT+1
ENDIF
RIA2(2) = ELEMENT
RINFOA(1) = 20
RINFOA(2) = 20
RINFOA(3) = 20
RINFOA(4) = 1
RINFOA(5) = 1
RINFOA(6) = 1
C IA== GLOBAL ROW INDEX
IA=(X-1)*IDIM*IDIM+(Y-1)*IDIM+(Z)
T3 = TIMEF()
CALL PDSPINS(AS,IA1,IA2,INFOA,DESC_A,
+ IA,1,RAS,RIA1,RIA2,RINFOA)
TINS = TINS + (TIMEF()-T3)
C Build RHS
IF (X==1) THEN
GLOB_Y=(Y-IDIM/2)*DELTAH
GLOB_Z=(Z-IDIM/2)*DELTAH
ZT(1) = EXP(-GLOB_Y**2-GLOB_Z**2)
ELSE IF ((Y==1).OR.(Y==IDIM).OR.(Z==1).OR.(Z==IDIM)) THEN
GLOB_X=3*(X-1)*DELTAH
GLOB_Y=(Y-IDIM/2)*DELTAH
GLOB_Z=(Z-IDIM/2)*DELTAH
ZT(1) = EXP(-GLOB_Y**2-GLOB_Z**2)*EXP(-GLOB_X)
ELSE
ZT(1) = 0.D0
ENDIF
CALL PDGEINS(1,B,NR,IA,1,1,1,ZT,1,DESC_A)
ZT(1) = 0.D0
CALL PDGEINS(1,T,NR,IA,1,1,1,ZT,1,DESC_A)
ENDIF
ENDDO
ENDDO
CALL BLACS_BARRIER(ICONTXT,'ALL')
T2 = TIMEF()
IF (MYPROW.EQ.0) THEN
WRITE(0,*) ' pspins time',TINS/1.D3
WRITE(0,*) ' Insert time',(T2-T1)/1.D3
ENDIF
CALL BLACS_BARRIER(ICONTXT,'ALL')
T1 = TIMEF()
CALL PDSPASB(AS,IA1,IA2,INFOA,DESC_A,
+ 'GEN ','DEF ',0,INFO)
CALL BLACS_BARRIER(ICONTXT,'ALL')
T2 = TIMEF()
IF (MYPROW.EQ.0) THEN
WRITE(0,*) ' Assembly time',(T2-T1)/1.D3
ENDIF
CALL PDGEASB(1,B,NR,DESC_A)
CALL PDGEASB(1,T,NR,DESC_A)
RETURN
END
C
C Get iteration parameters from the command line
C
SUBROUTINE GET_PARMS(ICONTXT,CMETHD,PREC,IDIM,
+ ISTOPC,ITMAX,ITRACE)
integer :: icontxt
Character*10 :: CMETHD, PREC
Integer :: IDIM, IRET, ISTOPC,ITMAX,ITRACE
Character*40 :: CHARBUF
INTEGER :: IARGC, NPROW, NPCOL, MYPROW, MYPCOL
EXTERNAL IARGC
INTEGER :: INTBUF(10), IP
CALL BLACS_GRIDINFO(ICONTXT, NPROW, NPCOL, MYPROW, MYPCOL)
IF (MYPROW==0) THEN
C Read command line parameters
IP=IARGC()
IF (IARGC().GE.3) THEN
CALL GETARG(1,CHARBUF)
READ(CHARBUF,*) CMETHD
CALL GETARG(2,CHARBUF)
READ(CHARBUF,*) PREC
C Convert strings in array
DO I = 1, LEN(CMETHD)
INTBUF(I) = IACHAR(CMETHD(I:I))
END DO
C Broadcast parameters to all processors
CALL IGEBS2D(ICONTXT,'ALL',' ',10,1,INTBUF,10)
DO I = 1, LEN(PREC)
INTBUF(I) = IACHAR(PREC(I:I))
END DO
C Broadcast parameters to all processors
CALL IGEBS2D(ICONTXT,'ALL',' ',10,1,INTBUF,10)
CALL GETARG(3,CHARBUF)
READ(CHARBUF,*) IDIM
IF (IARGC().GE.4) THEN
CALL GETARG(4,CHARBUF)
READ(CHARBUF,*) ISTOPC
ELSE
ISTOPC=1
ENDIF
IF (IARGC().GE.5) THEN
CALL GETARG(5,CHARBUF)
READ(CHARBUF,*) ITMAX
ELSE
ITMAX=500
ENDIF
IF (IARGC().GE.6) THEN
CALL GETARG(6,CHARBUF)
READ(CHARBUF,*) ITRACE
ELSE
ITRACE=0
ENDIF
C Broadcast parameters to all processors
CALL IGEBS2D(ICONTXT,'ALL',' ',1,1,IDIM,1)
CALL IGEBS2D(ICONTXT,'ALL',' ',1,1,ISTOPC,1)
CALL IGEBS2D(ICONTXT,'ALL',' ',1,1,ITMAX,1)
CALL IGEBS2D(ICONTXT,'ALL',' ',1,1,ITRACE,1)
WRITE(6,*)'Solving matrix: ELL1'
WRITE(6,*)'on grid',IDIM,'x',IDIM,'x',IDIM
WRITE(6,*)' with BLOCK data distribution, NP=',Np,
+ ' Preconditioner=',PREC,
+ ' Iterative methd=',CMETHD
ELSE
C Wrong number of parameter, print an error message and exit
CALL PR_USAGE(0)
CALL BLACS_ABORT(ICONTXT,-1)
STOP 1
ENDIF
ELSE
C Receive Parameters
CALL IGEBR2D(ICONTXT,'ALL',' ',10,1,INTBUF,10,0,0)
DO I = 1, 10
CMETHD(I:I) = ACHAR(INTBUF(I))
END DO
CALL IGEBR2D(ICONTXT,'ALL',' ',10,1,INTBUF,10,0,0)
DO I = 1, 10
PREC(I:I) = ACHAR(INTBUF(I))
END DO
CALL IGEBR2D(ICONTXT,'ALL',' ',1,1,IDIM,1,0,0)
CALL IGEBR2D(ICONTXT,'ALL',' ',1,1,ISTOPC,1,0,0)
CALL IGEBR2D(ICONTXT,'ALL',' ',1,1,ITMAX,1,0,0)
CALL IGEBR2D(ICONTXT,'ALL',' ',1,1,ITRACE,1,0,0)
END IF
RETURN
END
@PROCESS FREE(F90) INIT(F90PTR)
!
! This sample program shows how to build and solve a sparse linear
! system using the subroutines in the sparse section of Parallel
! ESSL; the matrices are read from file using the Harwell-Boeing
! exchange format. Details on the format and sample matrices are
! available from
!
! http://math.nist.gov/MatrixMarket/
!
! The user can choose between different data distribution strategies.
! These are equivalents to the HPF BLOCK and CYCLIC(N) distributions;
! they do not take into account the sparsity pattern of the input
! matrix.
!
PROGRAM HB_SAMPLE
USE F90SPARSE
USE MAT_DIST
USE READ_MAT
USE PARTRAND
USE PARTBCYC
IMPLICIT NONE
! Input parameters
CHARACTER*40 :: CMETHD, PREC, MTRX_FILE
CHARACTER*80 :: CHARBUF
DOUBLE PRECISION DDOT
EXTERNAL DDOT
EXTERNAL PART_BLOCK
INTEGER, PARAMETER :: IZERO=0, IONE=1
CHARACTER, PARAMETER :: ORDER='R'
REAL(KIND(1.D0)), POINTER,SAVE :: B_COL(:), X_COL(:), R_COL(:), &
& B_COL_GLOB(:), X_COL_GLOB(:), R_COL_GLOB(:), B_GLOB(:,:)
INTEGER :: IARGC
Real(Kind(1.d0)), Parameter :: Dzero = 0.d0, One = 1.d0
Real(Kind(1.d0)) :: TIMEF, T1, T2, TPREC, R_AMAX, B_AMAX,bb(1,1)
integer :: nrhs, nrow, nx1, nx2
External IARGC, TIMEF
integer bsze,overlap
common/part/bsze,overlap
! Sparse Matrices
TYPE(D_SPMAT) :: A, AUX_A
TYPE(D_PRECN) :: APRC
! Dense Matrices
REAL(KIND(1.D0)), POINTER :: AUX_B(:,:) , AUX1(:), AUX2(:)
! Communications data structure
TYPE(DESC_TYPE) :: DESC_A
! BLACS parameters
INTEGER :: NPROW, NPCOL, ICTXT, IAM, NP, MYPROW, MYPCOL
! Solver paramters
INTEGER :: ITER, ITMAX, IERR, ITRACE, IRCODE, IPART,&
& IPREC, METHD, ISTOPC
REAL(KIND(1.D0)) :: ERR, EPS
integer iparm(20)
real(kind(1.d0)) rparm(20)
! Other variables
INTEGER :: I,INFO,J
INTEGER :: INTERNAL, M,II,NNZERO
! common area
INTEGER M_PROBLEM, NPROC
! Initialize BLACS
CALL BLACS_PINFO(IAM, NP)
CALL BLACS_GET(IZERO, IZERO, ICTXT)
! Rectangular Grid, Np x 1
CALL BLACS_GRIDINIT(ICTXT, ORDER, NP, IONE)
CALL BLACS_GRIDINFO(ICTXT, NPROW, NPCOL, MYPROW, MYPCOL)
!
! Get parameters
!
CALL GET_PARMS(ICTXT,MTRX_FILE,CMETHD,PREC,&
& IPART,ISTOPC,ITMAX,ITRACE)
CALL BLACS_BARRIER(ICTXT,'A')
T1 = TIMEF()
! Read the input matrix to be processed and (possibly) the RHS
IF (IAM == 0) THEN
CALL READMAT(MTRX_FILE, AUX_A, ICTXT,B=AUX_B)
M_PROBLEM = AUX_A%M
CALL IGEBS2D(ICTXT,'A',' ',1,1,M_PROBLEM,1)
IF (SIZE(AUX_B,1).EQ.M_PROBLEM) THEN
! If any RHS were present, broadcast the first one
NRHS = 1
CALL IGEBS2D(ICTXT,'A',' ',1,1,NRHS,1)
CALL DGEBS2D(ICTXT,'A',' ',M_PROBLEM,1,AUX_B(:,1),M_PROBLEM)
ELSE
NRHS = 0
CALL IGEBS2D(ICTXT,'A',' ',1,1,NRHS,1)
ENDIF
ELSE
CALL IGEBR2D(ICTXT,'A',' ',1,1,M_PROBLEM,1,0,0)
CALL IGEBR2D(ICTXT,'A',' ',1,1,NRHS,1,0,0)
IF (NRHS.EQ.1) THEN
ALLOCATE(AUX_B(M_PROBLEM,1), STAT=IRCODE)
IF (IRCODE /= 0) THEN
WRITE(0,*) 'Memory allocation failure in HB_SAMPLE'
CALL BLACS_ABORT(ICTXT,-1)
STOP
ENDIF
CALL DGEBR2D(ICTXT,'A',' ',M_PROBLEM,1,AUX_B,M_PROBLEM,0,0)
ENDIF
END IF
IF (NRHS.EQ.1 ) THEN
B_COL_GLOB =>AUX_B(:,1)
ELSE
ALLOCATE(AUX_B(M_PROBLEM,1), STAT=IRCODE)
B_COL_GLOB =>AUX_B(:,1)
IF (IAM==0) THEN
DO I=1, M_PROBLEM
B_COL_GLOB(I) = REAL(I)*2.0/REAL(M_PROBLEM)
ENDDO
ENDIF
ENDIF
NPROC = NPROW
! Switch over different partition types
IF (IPART > 0 ) THEN
WRITE(6,*) 'Partition type: CYCLIC(NB)'
CALL SET_NB(IPART,0,0,ICTXT)
CALL MATDIST(AUX_A, A, PART_BCYC, ICTXT, &
& DESC_A,B_COL_GLOB,B_COL)
ELSE
SELECT CASE (IPART)
CASE (0)
WRITE(6,*) 'Partition type: BLOCK'
CALL MATDIST(AUX_A, A, PART_BLOCK, ICTXT, &
& DESC_A,B_COL_GLOB,B_COL)
CASE (-1)
WRITE(6,*) 'Partition type: RANDOM'
IF (IAM==0) THEN
CALL BUILD_RNDPART(AUX_A,NP)
ENDIF
CALL DISTR_RNDPART(0,0,ICTXT)
CALL MATDIST(AUX_A, A, PART_RAND, ICTXT, &
& DESC_A,B_COL_GLOB,B_COL)
CASE DEFAULT
WRITE(6,*) 'Partition type: BLOCK'
CALL MATDIST(AUX_A, A, PART_BLOCK, ICTXT, &
& DESC_A,B_COL_GLOB,B_COL)
END SELECT
ENDIF
CALL PGEALL(X_COL,DESC_A)
CALL PGEASB(X_COL,DESC_A)
T2 = TIMEF() - T1
CALL DGAMX2D(ICTXT, 'A', ' ', IONE, IONE, T2, IONE,&
& T1, T1, -1, -1, -1)
IF (IAM.EQ.0) THEN
WRITE(6,*) 'Time to Read and Partition Matrix : ',T2/1.D3
END IF
!
! Prepare the preconditioning matrix. Note the availability
! of optional parameters
!
IF (PREC(1:3) == 'ILU') THEN
IPREC = 2
ELSE IF (PREC(1:6) == 'DIAGSC') THEN
IPREC = 1
ELSE IF (PREC(1:4) == 'NONE') THEN
IPREC = 0
ELSE
WRITE(0,*) 'Unknown preconditioner'
CALL BLACS_ABORT(ICTXT,-1)
END IF
CALL BLACS_BARRIER(ICTXT,'A')
T1 = TIMEF()
CALL PSPGPR(IPREC,A,APRC,DESC_A,INFO=INFO)
TPREC = TIMEF()-T1
CALL DGAMX2D(ICTXT,'A',' ',IONE, IONE,TPREC,IONE,T1,T1,-1,-1,-1)
IF (IAM.EQ.0) WRITE(6,*) 'Preconditioner Time : ',TPREC/1.D3
IF (INFO /= 0) THEN
WRITE(0,*) 'Error in preconditioner :',INFO
CALL BLACS_ABORT(ICTXT,-1)
STOP
END IF
IPARM = 0
RPARM = 0.D0
EPS = 1.D-8
RPARM(1) = EPS
IPARM(2) = ISTOPC
IPARM(3) = ITMAX
IPARM(4) = ITRACE
IF (CMETHD(1:6).EQ.'CGSTAB') Then
IPARM(1)=1
ELSE IF (CMETHD(1:3).EQ.'CGS') THEN
IPARM(1)=2
ELSE IF (CMETHD(1:5).EQ.'TFQMR') THEN
IPARM(1)=3
ELSE
WRITE(0,*) 'Unknown method '
CALL BLACS_ABORT(ICTXT,-1)
END IF
CALL BLACS_BARRIER(ICTXT,'All')
T1 = TIMEF()
CALL PSPGIS(A,B_COL,X_COL,APRC,DESC_A,&
& IPARM=IPARM,RPARM=RPARM,INFO=IERR)
CALL BLACS_BARRIER(ICTXT,'All')
T2 = TIMEF() - T1
CALL DGAMX2D(ICTXT,'A',' ',IONE, IONE,T2,IONE,T1,T1,-1,-1,-1)
ITER=IPARM(5)
ERR = RPARM(2)
IF (IAM.EQ.0) THEN
WRITE(6,*) 'methd iprec istopc : ',METHD, IPREC, ISTOPC
WRITE(6,*) 'Number of iterations : ',ITER
WRITE(6,*) 'Time to Solve Matrix : ',T2/1.D3
WRITE(6,*) 'Time per iteration : ',T2/(1.D3*ITER)
WRITE(6,*) 'Error on exit : ',ERR
END IF
CALL PGEFREE(B_COL, DESC_A)
CALL PGEFREE(X_COL, DESC_A)
CALL PSPFREE(A, DESC_A)
CALL PSPFREE(APRC, DESC_A)
CALL PADFREE(DESC_A)
CALL BLACS_GRIDEXIT(ICTXT)
CALL BLACS_EXIT(0)
CONTAINS
!
! Get iteration parameters from the command line
!
SUBROUTINE GET_PARMS(ICONTXT,MTRX_FILE,CMETHD,PREC,IPART,&
& ISTOPC,ITMAX,ITRACE)
integer :: icontxt
Character*40 :: CMETHD, PREC, MTRX_FILE
Integer :: IRET, ISTOPC,ITMAX,ITRACE,IPART
Character*40 :: CHARBUF
INTEGER :: IARGC, NPROW, NPCOL, MYPROW, MYPCOL
EXTERNAL IARGC
INTEGER :: INPARMS(20), IP
CALL BLACS_GRIDINFO(ICONTXT, NPROW, NPCOL, MYPROW, MYPCOL)
IF (MYPROW==0) THEN
! Read Input Parameters
IF (IARGC().GE.3) THEN
CALL GETARG(1,CHARBUF)
READ(CHARBUF,*) MTRX_FILE
CALL GETARG(2,CHARBUF)
READ(CHARBUF,*) CMETHD
CALL GETARG(3,CHARBUF)
READ(CHARBUF,*) PREC
IF (IARGC().GE.4) THEN
CALL GETARG(4,CHARBUF)
READ(CHARBUF,*) IPART
ELSE
IPART = 0
ENDIF
IF (IARGC().GE.5) THEN
CALL GETARG(5,CHARBUF)
READ(CHARBUF,*) ITMAX
ELSE
ITMAX = 500
ENDIF
IF (IARGC().GE.6) THEN
CALL GETARG(6,CHARBUF)
READ(CHARBUF,*) ISTOPC
ELSE
ISTOPC = 1
ENDIF
IF (IARGC().GE.7) THEN
CALL GETARG(7,CHARBUF)
READ(CHARBUF,*) ITRACE
ELSE
ITRACE = 0
ENDIF
! Convert strings to integers
DO I = 1, 20
INPARMS(I) = IACHAR(MTRX_FILE(I:I))
END DO
! Broadcast parameters to all processors
CALL IGEBS2D(ICTXT,'A',' ',20,1,INPARMS,20)
! Convert strings in array
DO I = 1, 20
INPARMS(I) = IACHAR(CMETHD(I:I))
END DO
! Broadcast parameters to all processors
CALL IGEBS2D(ICTXT,'A',' ',20,1,INPARMS,20)
DO I = 1, 20
INPARMS(I) = IACHAR(PREC(I:I))
END DO
! Broadcast parameters to all processors
CALL IGEBS2D(ICTXT,'A',' ',20,1,INPARMS,20)
! Broadcast parameters to all processors
CALL IGEBS2D(ICTXT,'A',' ',1,1,IPART,1)
CALL IGEBS2D(ICTXT,'A',' ',1,1,ITMAX,1)
CALL IGEBS2D(ICTXT,'A',' ',1,1,ISTOPC,1)
CALL IGEBS2D(ICTXT,'A',' ',1,1,ITRACE,1)
ELSE
CALL PR_USAGE(0)
CALL BLACS_ABORT(ICTXT,-1)
STOP 1
END IF
ELSE
! Receive Parameters
CALL IGEBR2D(ICTXT,'A',' ',20,1,INPARMS,20,0,0)
DO I = 1, 20
MTRX_FILE(I:I) = ACHAR(INPARMS(I))
END DO
CALL IGEBR2D(ICTXT,'A',' ',20,1,INPARMS,20,0,0)
DO I = 1, 20
CMETHD(I:I) = ACHAR(INPARMS(I))
END DO
CALL IGEBR2D(ICTXT,'A',' ',20,1,INPARMS,20,0,0)
DO I = 1, 20
PREC(I:I) = ACHAR(INPARMS(I))
END DO
CALL IGEBR2D(ICTXT,'A',' ',1,1,IPART,1,0,0)
CALL IGEBR2D(ICTXT,'A',' ',1,1,ITMAX,1,0,0)
CALL IGEBR2D(ICTXT,'A',' ',1,1,ISTOPC,1,0,0)
CALL IGEBR2D(ICTXT,'A',' ',1,1,ITRACE,1,0,0)
END IF
END SUBROUTINE GET_PARMS
SUBROUTINE PR_USAGE(IOUT)
INTEGER IOUT
WRITE(IOUT, *) ' Number of parameters is incorrect!'
WRITE(IOUT, *) ' Use: hb_sample mtrx_file methd prec [ptype &
&itmax istopc itrace]'
WRITE(IOUT, *) ' Where:'
WRITE(IOUT, *) ' mtrx_file is stored in HB format'
WRITE(IOUT, *) ' methd may be: CGSTAB CGS TFQMR'
WRITE(IOUT, *) ' prec may be: ILU DIAGSC NONE'
WRITE(IOUT, *) ' ptype Partition strategy default 0'
WRITE(IOUT, *) ' >0: CYCLIC(ptype) '
WRITE(IOUT, *) ' 0: BLOCK partition '
WRITE(IOUT, *) ' -1: Random partition '
WRITE(IOUT, *) ' itmax Max iterations [500] '
WRITE(IOUT, *) ' istopc Stopping criterion [1] '
WRITE(IOUT, *) ' itrace 0 (no tracing, default) or '
WRITE(IOUT, *) ' >= 0 do tracing every ITRACE'
WRITE(IOUT, *) ' iterations '
END SUBROUTINE PR_USAGE
END PROGRAM HB_SAMPLE
This section shows sample parts programs.
C
C User defined function corresponding to an HPF BLOCK partition
C
SUBROUTINE PART_BLOCK(GLOBAL_INDX,N,NP,PV,NV)
IMPLICIT NONE
INTEGER, INTENT(IN) :: GLOBAL_INDX, N, NP
INTEGER, INTENT(OUT) :: NV
INTEGER, INTENT(OUT) :: PV(*)
INTEGER :: DIM_BLOCK
REAL(8), PARAMETER :: PC=0.0D0
REAL(8) :: DDIFF
INTEGER :: IB1, IB2, IPV
DIM_BLOCK = (N + NP - 1)/NP
NV = 1
PV(NV) = (GLOBAL_INDX - 1) / DIM_BLOCK
IPV = PV(1)
IB1 = IPV * DIM_BLOCK + 1
IB2 = (IPV+1) * DIM_BLOCK
DDIFF = DBLE(ABS(GLOBAL_INDX-IB1))/DBLE(DIM_BLOCK)
IF (DDIFF < PC/2) THEN
C
C Overlap at the beginning of a block, with the previous proc
C
IF (IPV>0) THEN
NV = NV + 1
PV(NV) = IPV - 1
ENDIF
ENDIF
DDIFF = DBLE(ABS(GLOBAL_INDX-IB2))/DBLE(DIM_BLOCK)
IF (DDIFF < PC/2) THEN
C
C Overlap at the end of a block, with the next proc
C
IF (IPV<(NP-1)) THEN
NV = NV + 1
PV(NV) = IPV + 1
ENDIF
ENDIF
RETURN
END
@process free(f90)
MODULE PARTBCYC
PUBLIC PART_BCYC, SET_NB
PRIVATE
INTEGER, SAVE :: BLOCK_SIZE
CONTAINS
!
! User defined subroutine corresponding to an HPF CYCLIC(NB)
! data distribution
!
SUBROUTINE PART_BCYC(GLOBAL_INDX,N,NP,PV,NV)
IMPLICIT NONE
INTEGER, INTENT(IN) :: GLOBAL_INDX, N, NP
INTEGER, INTENT(OUT) :: NV
INTEGER, INTENT(OUT) :: PV(*)
NV = 1
PV(NV) = MOD((((GLOBAL_INDX+BLOCK_SIZE-1)/BLOCK_SIZE)-1),NP)
RETURN
END SUBROUTINE PART_BCYC
SUBROUTINE SET_NB(NB, RROOT, CROOT, ICTXT)
INTEGER :: RROOT, CROOT, ICTXT
INTEGER :: N, MER, MEC, NPR, NPC
CALL BLACS_GRIDINFO(ICTXT,NPR,NPC,MER,MEC)
IF (.NOT.((RROOT>=0).AND.(RROOT<NPR).AND.&
& (CROOT>=0).AND.(CROOT<NPC))) THEN
WRITE(0,*) 'Fatal error in SET_NB: invalid ROOT ',&
& 'coordinates '
CALL BLACS_ABORT(ICTXT,-1)
RETURN
ENDIF
IF ((MER==RROOT).AND.(MEC==CROOT)) THEN
IF (NB < 1) THEN
WRITE(0,*) 'Fatal error in SET_NB: invalid NB'
CALL BLACS_ABORT(ICTXT,-1)
RETURN
ENDIF
CALL IGEBS2D(ICTXT,'A',' ',1,1,NB,1)
ELSE
CALL IGEBR2D(ICTXT,'A',' ',1,1,NB,1,RROOT,CROOT)
ENDIF
BLOCK_SIZE = NB
RETURN
END SUBROUTINE SET_NB
END MODULE PARTBCYC
@process free(f90) init(f90ptr)
!
! Purpose:
! Provide a set of subroutines to define a data distribution based on
! a random number generator.
! This partition does *not* generally give good performance; it may be
! useful as a model to implement a graph partitioning based
! distribution; to do this you need to alter the BUILD_RNDPART
! subroutine to make it call your favorite graph partition subroutine
! instead of the random number generator.
!
! Subroutines:
!
! BUILD_RNDPART(A,NPARTS): This subroutine will be called by the root
! process to build define the data distribution mapping.
! Input parameters:
! TYPE(D_SPMAT) :: A The input matrix. The coefficients are
! ignored; only the structure is used.
! INTEGER :: NPARTS How many parts we are requiring to the
! partition utility
!
!
! DISTR_RNDPART(RROOT,CROOT,ICTXT): This subroutine will be called by
! all processes to distribute the information computed by the root
! process, to be used subsequently.
!
!
! PART_RAND : The subroutine to be passed to PESSL sparse library;
! uses information prepared by the previous two subroutines.
!
MODULE PARTRAND
PUBLIC PART_RAND, BUILD_RNDPART, DISTR_RNDPART
PRIVATE
INTEGER, POINTER, SAVE :: RAND_VECT(:)
CONTAINS
SUBROUTINE PART_RAND(GLOBAL_INDX,N,NP,PV,NV)
INTEGER, INTENT(IN) :: GLOBAL_INDX, N, NP
INTEGER, INTENT(OUT) :: NV
INTEGER, INTENT(OUT) :: PV(*)
IF (.NOT.ASSOCIATED(RAND_VECT)) THEN
WRITE(0,*) 'Fatal error in PART_RAND: vector RAND_VECT ',&
& 'not initialized'
RETURN
ENDIF
IF ((GLOBAL_INDX<1).OR.(GLOBAL_INDX > SIZE(RAND_VECT))) THEN
WRITE(0,*) 'Fatal error in PART_RAND: index GLOBAL_INDX ',&
& 'outside RAND_VECT bounds'
RETURN
ENDIF
NV = 1
PV(NV) = RAND_VECT(GLOBAL_INDX)
RETURN
END SUBROUTINE PART_RAND
SUBROUTINE DISTR_RNDPART(RROOT, CROOT, ICTXT)
INTEGER :: RROOT, CROOT, ICTXT
INTEGER :: N, MER, MEC, NPR, NPC
CALL BLACS_GRIDINFO(ICTXT,NPR,NPC,MER,MEC)
IF (.NOT.((RROOT>=0).AND.(RROOT<NPR).AND.&
& (CROOT>=0).AND.(CROOT<NPC))) THEN
WRITE(0,*) 'Fatal error in DISTR_RNDPART: invalid ROOT ',&
& 'coordinates '
CALL BLACS_ABORT(ICTXT,-1)
RETURN
ENDIF
IF ((MER == RROOT) .AND.(MEC == CROOT)) THEN
IF (.NOT.ASSOCIATED(RAND_VECT)) THEN
WRITE(0,*) 'Fatal error in DISTR_RNDPART: vector RAND_VECT ',&
& 'not initialized'
CALL BLACS_ABORT(ICTXT,-1)
RETURN
ENDIF
N = SIZE(RAND_VECT)
CALL IGEBS2D(ICTXT,'All',' ',1,1,N,1)
CALL IGEBS2D(ICTXT,'All',' ',N,1,RAND_VECT,N)
ELSE
CALL IGEBR2D(ICTXT,'All',' ',1,1,N,1,RROOT,CROOT)
IF (ASSOCIATED(RAND_VECT)) THEN
DEALLOCATE(RAND_VECT)
ENDIF
ALLOCATE(RAND_VECT(N),STAT=INFO)
IF (INFO /= 0) THEN
WRITE(0,*) 'Fatal error in DISTR_RNDPART: memory allocation ',&
& ' failure.'
RETURN
ENDIF
CALL IGEBR2D(ICTXT,'All',' ',N,1,RAND_VECT,N,RROOT,CROOT)
ENDIF
RETURN
END SUBROUTINE DISTR_RNDPART
SUBROUTINE BUILD_RNDPART(A,NPARTS)
USE F90SPARSE
TYPE(D_SPMAT) :: A
INTEGER :: NPARTS
INTEGER :: N, I, IB, II
INTEGER, PARAMETER :: NB=512
REAL(KIND(1.D0)), PARAMETER :: SEED=12345.D0
REAL(KIND(1.D0)) :: XV(NB)
N = A%M
IF (ASSOCIATED(RAND_VECT)) THEN
DEALLOCATE(RAND_VECT)
ENDIF
ALLOCATE(RAND_VECT(N),STAT=INFO)
IF (INFO /= 0) THEN
WRITE(0,*) 'Fatal error in BUILD_RNDPART: memory allocation ',&
& ' failure.'
RETURN
ENDIF
IF (NPARTS.GT.1) THEN
DO I=1, N, NB
IB = MIN(N-I+1,NB)
CALL DURAND(SEED,IB,XV)
DO II=1, IB
RAND_VECT(I+II-1) = MIN(NPARTS-1,INT(XV(II)*NPARTS))
ENDDO
ENDDO
ELSE
DO I=1, N
RAND_VECT(I) = 0
ENDDO
ENDIF
RETURN
END SUBROUTINE BUILD_RNDPART
END MODULE PARTRAND
@PROCESS FREE(F90) INIT(F90PTR)
!
! READ_MAT subroutine reads a matrix and its right hand sides,
! all stored in a BCS format file. The B field is optional,.
!
! Character :: filename*20
! On Entry: name of file to be processed.
! On Exit : unchanged.
!
! Type(D_SPMAT) :: A
! On Entry: fresh variable.
! On Exit : will contain the global sparse matrix as follows:
! A%AS for coefficient values
! A%IA1 for column indices
! A%IA2 for row pointers
! A%M for number of global matrix rows
! A%K for number of global matrix columns
!
! Integer :: ICTXT
! On Entry: BLACS context.
! On Exit : unchanged.
!
! Real(Kind(1.D0)), Pointer, Optional :: B(:,:)
! On Entry: fresh variable.
! On Exit: will contain right hand side(s).
!
! Integer, Optional :: inroot
! On Entry: Index of root processor (default: 0)
! On Exit : unchanged.
!
! Real(Kind(1.D0)), Pointer, Optional :: indwork(:)
! On Entry/Exit: Double Precision Work Area.
!
! Integer, Pointer, Optional :: iniwork()
! On Entry/Exit: Integer Work Area.
!
MODULE READ_MAT
PUBLIC READMAT
CONTAINS
SUBROUTINE READMAT (FILENAME, A, ICTXT, B, INROOT,&
& INDWORK, INIWORK)
USE F90SPARSE
! Parameters
IMPLICIT NONE
REAL(KIND(1.D0)), POINTER, OPTIONAL :: B(:,:)
INTEGER :: ICTXT
TYPE(D_SPMAT) :: A
CHARACTER :: FILENAME*(*)
INTEGER, OPTIONAL :: INROOT
REAL(KIND(1.0D0)), POINTER, OPTIONAL :: INDWORK(:)
INTEGER, POINTER, OPTIONAL :: INIWORK(:)
! Local Variables
INTEGER, PARAMETER :: INFILE = 2
CHARACTER :: MXTYPE*3, KEY*8, TITLE*72,&
& INDFMT*16, PTRFMT*16, RHSFMT*20, VALFMT*20, RHSTYP
INTEGER :: INDCRD, PTRCRD, TOTCRD,&
& VALCRD, RHSCRD, NROW, NCOL, NNZERO, NELTVL, NRHS, NRHSIX
REAL(KIND(1.0D0)), POINTER :: AS_LOC(:), DWORK(:)
INTEGER, POINTER :: IA1_LOC(:), IA2_LOC(:), IWORK(:)
INTEGER :: D_ALLOC, I_ALLOC, IRCODE, I,&
& J, LIWORK, LDWORK, ROOT, NPROW, NPCOL, MYPROW, MYPCOL
IF (PRESENT(INROOT)) THEN
ROOT = INROOT
ELSE
ROOT = 0
END IF
CALL BLACS_GRIDINFO(ICTXT, NPROW, NPCOL, MYPROW, MYPCOL)
IF (MYPROW == ROOT) THEN
WRITE(*, *) 'Start read_matrix'
! Open Input File
OPEN(INFILE,FILE=FILENAME, STATUS='OLD', ERR=901, ACTION="READ")
READ(INFILE,FMT='(A72,A8,/,5I14,/,A3,11X,4I14,/,2A16,2A20)',&
& END=902) TITLE, KEY, TOTCRD, PTRCRD,INDCRD, VALCRD,&
& RHSCRD, MXTYPE, NROW, NCOL, NNZERO, NELTVL,&
& PTRFMT, INDFMT, VALFMT, RHSFMT
A%M = NROW
A%N = NCOL
A%FIDA = 'CSR'
IF (RHSCRD>0) READ(INFILE, FMT='(A1,13X,2I14)',&
& END=902) RHSTYP, NRHS, NRHSIX
IF (MXTYPE == 'RUA') THEN
ALLOCATE(A%AS(NNZERO), A%IA1(NNZERO), A%IA2(NROW + 1),&
& STAT = IRCODE)
IF (IRCODE <> 0) GOTO 993
READ(INFILE,FMT=PTRFMT,END=902) (A%IA2(I), I=1,NROW+1)
READ(INFILE,FMT=INDFMT,END=902) (A%IA1(I), I=1,NNZERO)
READ(INFILE,FMT=VALFMT,END=902) (A%AS(I), I=1,NNZERO)
ELSE IF (MXTYPE == 'RSA') THEN
! We are generally working with non-symmetric matrices, so
! we de-symmetrize what we are about to read
ALLOCATE(A%AS(2*NNZERO),A%IA1(2*NNZERO),&
& A%IA2(NROW+1),AS_LOC(2*NNZERO),&
& IA1_LOC(2*NNZERO),IA2_LOC(NROW+1),STAT=IRCODE)
IF (IRCODE <> 0) GOTO 993
READ(INFILE,FMT=PTRFMT,END=902) (IA2_LOC(I), I=1,NROW+1)
READ(INFILE,FMT=INDFMT,END=902) (IA1_LOC(I), I=1,NNZERO)
READ(INFILE,FMT=VALFMT,END=902) (AS_LOC(I), I=1,NNZERO)
LDWORK = MAX(NROW + 1, 2 * NNZERO)
IF (PRESENT(INDWORK)) THEN
IF (SIZE(INDWORK) >= LDWORK) THEN
DWORK => INDWORK
D_ALLOC = 0
ELSE
ALLOCATE(DWORK(LDWORK), STAT = IRCODE)
D_ALLOC = 1
END IF
ELSE
ALLOCATE(DWORK(LDWORK), STAT = IRCODE)
D_ALLOC = 1
END IF
IF (IRCODE <> 0) GOTO 993
LIWORK = NROW + 1
IF (PRESENT(INIWORK)) THEN
IF (SIZE(INIWORK) >= LIWORK) THEN
IWORK => INIWORK
I_ALLOC = 0
ELSE
ALLOCATE(IWORK(LIWORK), STAT = IRCODE)
I_ALLOC = 1
END IF
ELSE
ALLOCATE(IWORK(LIWORK), STAT = IRCODE)
I_ALLOC = 1
END IF
IF (IRCODE <> 0) GOTO 993
! After this call NNZERO contains the actual value for
! desymetrized matrix
CALL DESYM(NROW, AS_LOC, IA1_LOC, IA2_LOC, A%AS, A%IA1,&
& A%IA2, IWORK, DWORK, NNZERO, 1)
DEALLOCATE(AS_LOC, IA1_LOC, IA2_LOC)
IF (D_ALLOC == 1) DEALLOCATE(DWORK)
IF (I_ALLOC == 1) DEALLOCATE(IWORK)
ELSE
WRITE(0,*) 'READ_MATRIX: matrix type not yet supported'
CALL BLACS_ABORT(ICTXT, 1)
END IF
! Read Right Hand Sides
IF (PRESENT(B) .AND. (NRHS > 0)) THEN
WRITE(0,*) 'Reading RHS'
IF (RHSTYP == 'F') THEN
ALLOCATE(B(NROW, NRHS), STAT = IRCODE)
IF (IRCODE <> 0) GOTO 993
READ(INFILE,FMT=RHSFMT,END=902) ((B(I,J), I=1,NROW),J=1,NRHS)
ELSE !(RHSTYP <> 'F')
WRITE(0,*) 'READ_MATRIX: unsupported RHS type'
END IF
END IF
CLOSE(INFILE)
WRITE(*,*) 'End READ_MATRIX'
END IF
RETURN
! Open failed
901 WRITE(0,*) 'READ_MATRIX: Could not open file ',&
& INFILE,' for input'
CALL BLACS_ABORT(ICTXT, 1)
! Unexpected End of File
902 WRITE(0,*) 'READ_MATRIX: Unexpected end of file ',INFILE,&
& ' during input'
CALL BLACS_ABORT(ICTXT, 1)
! Allocation Failed
993 WRITE(0,*) 'READ_MATRIX: Memory allocation failure'
CALL BLACS_ABORT(ICTXT, 1)
END SUBROUTINE READMAT
END MODULE READ_MAT
@process free(f90) init(f90ptr)
MODULE MAT_DIST
PUBLIC MATDIST
CONTAINS
SUBROUTINE MATDIST (A_GLOB, A, PARTS, ICONTXT, DESC_A,&
& B_GLOB, B, INROOT)
!
! An utility subroutine to distribute a matrix among processors
! according to a user defined data distribution, using PESSL
! sparse matrix subroutines.
!
! Type(D_SPMAT) :: A_GLOB
! On Entry: this contains the global sparse matrix as follows:
! A%FIDA =='CSR'
! A%AS for coefficient values
! A%IA1 for column indices
! A%IA2 for row pointers
! A%M for number of global matrix rows
! A%K for number of global matrix columns
! On Exit : undefined, with unassociated pointers.
!
! Type(D_SPMAT) :: A
! On Entry: fresh variable.
! On Exit : this will contain the local sparse matrix.
!
! INTERFACE PARTS
! ! .....user passed subroutine.....
! SUBROUTINE PARTS(GLOBAL_INDX,N,NP,PV,NV)
! IMPLICIT NONE
! INTEGER, INTENT(IN) :: GLOBAL_INDX, N, NP
! INTEGER, INTENT(OUT) :: NV
! INTEGER, INTENT(OUT) :: PV(*)
!
! END SUBROUTINE PARTS
! END INTERFACE
! On Entry: subroutine providing user defined data distribution.
! For each GLOBAL_INDX the subroutine should return
! the list PV of all processes owning the row with
! that index; the list will contain NV entries.
! Usually NV=1; if NV >1 then we have an overlap in the data
! distribution.
!
! Integer :: ICONTXT
! On Entry: BLACS context.
! On Exit : unchanged.
!
! Type (DESC_TYPE) :: DESC_A
! On Entry: fresh variable.
! On Exit : the updated array descriptor
!
! Real(Kind(1.D0)), Pointer, Optional :: B_GLOB(:)
! On Entry: this contains right hand side.
! On Exit :
!
! Real(Kind(1.D0)), Pointer, Optional :: B(:)
! On Entry: fresh variable.
! On Exit : this will contain the local right hand side.
!
! Integer, Optional :: inroot
! On Entry: specifies processor holding A_GLOB. Default: 0
! On Exit : unchanged.
!
!
Use F90SPARSE
Implicit None
! Parameters
Type(D_SPMAT) :: A_GLOB
Real(Kind(1.D0)), Pointer :: B_GLOB(:)
Integer :: ICONTXT
Type(D_SPMAT) :: A
Real(Kind(1.D0)), Pointer :: B(:)
Type (DESC_TYPE) :: DESC_A
INTEGER, OPTIONAL :: INROOT
INTERFACE PARTS
! .....user passed subroutine.....
SUBROUTINE PARTS(GLOBAL_INDX,N,NP,PV,NV)
IMPLICIT NONE
INTEGER, INTENT(IN) :: GLOBAL_INDX, N, NP
INTEGER, INTENT(OUT) :: NV
INTEGER, INTENT(OUT) :: PV(*)
END SUBROUTINE PARTS
END INTERFACE
! Local variables
Integer :: NPROW, NPCOL, MYPROW, MYPCOL
Integer :: IRCODE, LENGTH_ROW, I_COUNT, J_COUNT,&
& K_COUNT, BLOCKDIM, ROOT, LIWORK, NROW, NCOL, NNZERO, NRHS,&
& I,J,K, LL, INFO
Integer, Pointer :: IWORK(:)
CHARACTER :: AFMT*5, atyp*5
Type(D_SPMAT) :: BLCK
! Executable statements
IF (PRESENT(INROOT)) THEN
ROOT = INROOT
ELSE
ROOT = 0
END IF
CALL BLACS_GRIDINFO(ICONTXT, NPROW, NPCOL, MYPROW, MYPCOL)
IF (MYPROW == ROOT) THEN
! Extract information from A_GLOB
IF (A_GLOB%FIDA /= 'CSR') THEN
WRITE(0,*) 'Unsupported input matrix format'
CALL BLACS_ABORT(ICONTXT,-1)
ENDIF
NROW = A_GLOB%M
NCOL = A_GLOB%N
IF (NROW /= NCOL) THEN
WRITE(0,*) 'A rectangular matrix ? ',NROW,NCOL
CALL BLACS_ABORT(ICONTXT,-1)
ENDIF
NNZERO = Size(A_GLOB%AS)
NRHS = 1
! Broadcast informations to other processors
CALL IGEBS2D(ICONTXT, 'A', ' ', 1, 1, NROW, 1)
CALL IGEBS2D(ICONTXT, 'A', ' ', 1, 1, NCOL, 1)
CALL IGEBS2D(ICONTXT, 'A', ' ', 1, 1, NNZERO, 1)
CALL IGEBS2D(ICONTXT, 'A', ' ', 1, 1, NRHS, 1)
ELSE !(MYPROW <> root)
! Receive informations
CALL IGEBR2D(ICONTXT, 'A', ' ', 1, 1, NROW, 1, ROOT, 0)
CALL IGEBR2D(ICONTXT, 'A', ' ', 1, 1, NCOL, 1, ROOT, 0)
CALL IGEBR2D(ICONTXT, 'A', ' ', 1, 1, NNZERO, 1, ROOT, 0)
CALL IGEBR2D(ICONTXT, 'A', ' ', 1, 1, NRHS, 1, ROOT, 0)
END IF
! Allocate integer work area
LIWORK = MAX(NPROW, NROW + NCOL)
ALLOCATE(IWORK(LIWORK), STAT = IRCODE)
IF (IRCODE <> 0) THEN
WRITE(0,*) 'MATDIST Allocation failed'
RETURN
ENDIF
IF (MYPROW == ROOT) THEN
WRITE (*, FMT = *) 'Start matdist'
ENDIF
CALL PADALL(NROW,PARTS,DESC_A,ICONTXT)
CALL PSPALL(A,DESC_A,NNZ=NNZERO/NPROW)
CALL PGEALL(B,DESC_A)
! Prepare the local
ALLOCATE(BLCK%AS(NCOL),BLCK%IA1(NCOL),BLCK%IA2(2),STAT=IRCODE)
IF (IRCODE /= 0) THEN
WRITE(0,*) 'Error on allocating BLCK'
CALL BLACS_ABORT(ICONTXT,-1)
STOP
ENDIF
BLCK%M = 1
BLCK%N = NCOL
BLCK%FIDA = 'CSR'
Do I_COUNT = 1, NROW
CALL PARTS(I_COUNT,NROW,NPROW,IWORK, LENGTH_ROW)
! Here processors are counted 1..NPROW
DO J_COUNT = 1, LENGTH_ROW
K_COUNT = IWORK(J_COUNT)
IF (MYPROW == ROOT) THEN
BLCK%IA2(1) = 1
BLCK%IA2(2) = 1
DO J = A_GLOB%IA2(I_COUNT), A_GLOB%IA2(I_COUNT+1)-1
BLCK%AS(BLCK%IA2(2)) = A_GLOB%AS(J)
BLCK%IA1(BLCK%IA2(2)) = A_GLOB%IA1(J)
BLCK%IA2(2) =BLCK%IA2(2) + 1
ENDDO
LL = BLCK%IA2(2) - 1
IF (K_COUNT == MYPROW) THEN
BLCK%INFOA(1) = LL
BLCK%INFOA(2) = LL
BLCK%INFOA(3) = 2
BLCK%INFOA(4) = 1
BLCK%INFOA(5) = 1
BLCK%INFOA(6) = 1
CALL PSPINS(A,I_COUNT,1,BLCK,DESC_A)
CALL PGEINS(B,B_GLOB(I_COUNT:I_COUNT),DESC_A,I_COUNT)
ELSE
CALL IGESD2D(ICONTXT,1,1,LL,1,K_COUNT,0)
CALL IGESD2D(ICONTXT,LL,1,BLCK%IA1,LL,K_COUNT,0)
CALL DGESD2D(ICONTXT,LL,1,BLCK%AS,LL,K_COUNT,0)
CALL DGESD2D(ICONTXT,1,1,B_GLOB(I_COUNT),1,K_COUNT,0)
CALL IGERV2D(ICONTXT,1,1,LL,1,K_COUNT,0)
ENDIF
ELSE IF (MYPROW /= ROOT) THEN
IF (K_COUNT == MYPROW) THEN
CALL IGERV2D(ICONTXT,1,1,LL,1,ROOT,0)
BLCK%IA2(1) = 1
BLCK%IA2(2) = LL+1
CALL IGERV2D(ICONTXT,LL,1,BLCK%IA1,LL,ROOT,0)
CALL DGERV2D(ICONTXT,LL,1,BLCK%AS,LL,ROOT,0)
CALL DGERV2D(ICONTXT,1,1,B_GLOB(I_COUNT),1,ROOT,0)
CALL IGESD2D(ICONTXT,1,1,LL,1,ROOT,0)
CALL PSPINS(A,I_COUNT,1,BLCK,DESC_A)
CALL PGEINS(B,B_GLOB(I_COUNT:I_COUNT),DESC_A,I_COUNT)
ENDIF
ENDIF
END DO
END DO
! Default storage format for sparse matrix; we do not
! expect duplicated entries.
AFMT = 'DEF'
ATYP = 'GEN'
CALL PSPASB(A,DESC_A,INFO=INFO,MTYPE=ATYP,STOR=AFMT,DUPFLAG=2)
CALL PGEASB(B,DESC_A)
DEALLOCATE(BLCK%AS,BLCK%IA1,BLCK%IA2,IWORK)
IF (MYPROW == root) Write (*, FMT = *) 'End matdist'
RETURN
END SUBROUTINE MATDIST
END MODULE MAT_DIST
SUBROUTINE DESYM(NROW,A,JA,IA,AS,JAS,IAS,IAW,WORK,NNZERO,
+ VALUE)
IMPLICIT NONE
C .. Scalar Arguments ..
INTEGER NROW,NNZERO,VALUE,INDEX
C .. Array Arguments ..
DOUBLE PRECISION A(*),AS(*),WORK(*)
INTEGER IA(*),IAS(*),JAS(*),JA(*),IAW(*)
C .. Local Scalars ..
INTEGER I,IAW1,IAW2,IAWT,J,JPT,K,KPT,LDIM,COUNT,JS,BUFI
C REAL*8 BUF
C ..
DO I=1,NROW
IAW(I)=0
END DO
C ....Compute element belonging to each row in output matrix.....
DO I=1,NROW
DO J=IA(I),IA(I+1)-1
IAW(I)=IAW(I)+1
IF (JA(J).NE.I) IAW(JA(J))=IAW(JA(J))+1
END DO
END DO
IAS(1)=1
DO I=1,NROW
IAS(I+1)=IAS(I)+IAW(I)
IAW(I)=0
END DO
C
C .....Computing values array AS and column array indices JAS....
C
DO I=1,NROW
DO J=IA(I),IA(I+1)-1
IF (VALUE.NE.0) THEN
AS(IAS(I)+IAW(I))=A(J)
ENDIF
JAS(IAS(I)+IAW(I))=JA(J)
IAW(I)=IAW(I)+1
IF (I.NE.JA(J)) THEN
IF (VALUE.NE.0) THEN
AS(IAS(JA(J))+IAW(JA(J)))=A(J)
ENDIF
NNZERO=NNZERO+1
JAS(IAS(JA(J))+IAW(JA(J)))=I
IAW(JA(J))=IAW(JA(J))+1
END IF
END DO
END DO
C ......Sorting output arrays by column index......
C .....the IAS index not must be modified.....
C
DO I=1,NROW
CALL ISORTX(JAS(IAS(I)),1,IAS(I+1)-IAS(I),IAW)
INDEX=IAS(I)-1
IF (VALUE.NE.0) THEN
DO J=1,IAS(I+1)-IAS(I)
WORK(J)=AS(IAW(J)+INDEX)
END DO
DO J=1,IAS(I+1)-IAS(I)
AS(J+INDEX)=WORK(J)
END DO
ENDIF
C ....column indices are already sorted by ISORTX...
ENDDO
RETURN
END
[ Top of Page | Previous Page | Next Page | Table of Contents | Index ]