Parallel Engineering and Scientific Subroutine Library for AIX Version 2 Release 3: Guide and Reference

PDSYR2K, PZSYR2K, and PZHER2K--Rank-2K Update of a Real or Complex Symmetric or a Complex Hermitian Matrix

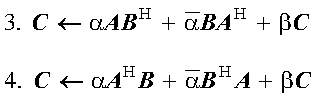
PDSYR2K and PZSYR2K compute one of the following rank-2k updates:

1. C <-- alphaAB^T+alphaBA^T+betaC

2. C <-- alphaA^TB+alphaB^TA+betaC

PZHER2K computes one of the following rank-2k updates:

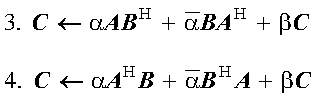
Rank-2K Update Graphic

where, in the formulas above:

A represents the global general submatrix:

For trans = 'N', it is A_{ia:ia+n-1,
ja:ja+k-1}.
For trans = 'T' or 'C', it is A_{ia:ia+k-1,
ja:ja+n-1}.

B represents the global general submatrix:

For trans = 'N', it is B_{ib:ib+n-1,
jb:jb+k-1}.
For trans = 'T' or 'C', it is B_{ib:ib+k-1,
jb:jb+n-1}.

C represents the global submatrix C_{ic:ic+n-1,
jc:jc+n-1}.

alpha and beta are scalars.

Note:: No data should be moved to form A^T, A^H, B^T, or B^H; that is, the A and B matrices should always be stored in their untransposed forms.

In the following two cases, no computation is performed and the subroutine returns after doing some parameter checking:

n = 0
beta is one, and alpha is zero or k = 0.

See references [14] and [15].

Table 52. Data Types

A, B, C, alpha	beta	Subprogram
Long-precision real	Long-precision real	PDSYR2K
Long-precision complex	Long-precision complex	PZSYR2K
Long-precision complex	Long-precision real	PZHER2K

Syntax

Fortran	CALL PDSYR2K \| PZSYR2K \| PZHER2K (`uplo`, `trans`, `n`, `k`, `alpha`, `a`, `ia`, `ja`, `desc_a`, `b`, `ib`, `jb`, `desc_b`, `beta`, `c`, `ic`, `jc`, `desc_c`)
C and C++	pdsyr2k \| pzsyr2k \| pzher2k (`uplo`, `trans`, `n`, `k`, `alpha`, `a`, `ia`, `ja`, `desc_a`, `b`, `ib`, `jb`, `desc_b`, `beta`, `c`, `ic`, `jc`, `desc_c`);

On Entry

uplo

indicates whether the upper or lower triangular part of the global submatrix C is referenced, where:

If uplo = 'U', the upper triangular part is referenced.

If uplo = 'L', the lower triangular part is referenced.

Scope: global

Specified as: a single character; uplo = 'U' or 'L'.

trans

indicates which computation is performed, where:

If trans = 'N', A and B are used.

If trans = 'T', A^T and B^T are used.

If trans = 'C', A^H and B^H are used.

Scope: global

Specified as: a single character, where:

For PDSYR2K, it must be 'N', 'T', or 'C'.

For PZSYR2K, it must be 'N' or 'T'.

For PZHER2K, it must be 'N' or 'C'.

n

is the order of the global submatrix C used in the computation, and:

If trans = 'N', it is the number of rows in submatrices A and B used in the computation.

If trans = 'T' or 'C', it is the number of columns in submatrices A and B used in the computation.

Scope: global

Specified as: a fullword integer; n >= 0.

k

has the following meaning:

If trans = 'N', it is the number of columns in submatrices A and B used in the computation.

If trans = 'T' or 'C', it is the number of rows in submatrices A and B used in the computation.

Scope: global

Specified as: a fullword integer; k >= 0.

alpha

is the scalar alpha.

Scope: global

Specified as: a number of the data type indicated in Table 52.

a

is the local part of the global general matrix A. This identifies the first element of the local array A. This subroutine computes the location of the first element of the local subarray used, based on ia, ja, desc_a, p, q, myrow, and mycol; therefore:

If trans = 'N', the leading LOCp(ia+n-1) by LOCq(ja+k-1) part of the local array A must contain the local pieces of the leading ia+n-1 by ja+k-1 part of the global matrix.
If trans = 'T' or 'C', the leading LOCp(ia+k-1) by LOCq(ja+n-1) part of the local array A must contain the local pieces of the leading ia+k-1 by ja+n-1 part of the global matrix.

Note:: No data should be moved to form A^T or A^H; that is, the matrix A should always be stored in its untransposed form.

Scope: local

Specified as: an LLD_A by (at least) LOCq(N_A) array, containing numbers of the data type indicated in Table 52. Details about the block-cyclic data distribution of global matrix A are stored in desc_a.

ia

is the row index of the global matrix A, identifying the first row of the submatrix A.

Scope: global

Specified as: a fullword integer; 1 <= ia <= M_A, and:

If trans = 'N', then ia+n-1 <= M_A.

If trans = 'T' or 'C', then ia+k-1 <= M_A.

ja

is the column index of the global matrix A, identifying the first column of the submatrix A.

Scope: global

Specified as: a fullword integer; 1 <= ja <= N_A, and:

If trans = 'N', then ja+k-1 <= N_A.

If trans = 'T' or 'C', then ja+n-1 <= N_A.

desc_a

is the array descriptor for global matrix A, described in the following table:

`desc_a`	Name	Description	Limits	Scope
1	DTYPE_A	Descriptor type	DTYPE_A=1	Global
2	CTXT_A	BLACS context	Valid value, as returned by BLACS_GRIDINIT or BLACS_GRIDMAP	Global
3	M_A	Number of rows in the global matrix	If `n` = 0 or `k` = 0: M_A >= 0 Otherwise: M_A >= 1	Global
4	N_A	Number of columns in the global matrix	If `n` = 0 or `k` = 0: N_A >= 0 Otherwise: N_A >= 1	Global
5	MB_A	Row block size	MB_A >= 1	Global
6	NB_A	Column block size	NB_A >= 1	Global
7	RSRC_A	The process row of the `p` × `q` grid over which the first row of the global matrix is distributed	0 <= RSRC_A < `p`	Global
8	CSRC_A	The process column of the `p` × `q` grid over which the first column of the global matrix is distributed	0 <= CSRC_A < `q`	Global
9	LLD_A	The leading dimension of the local array	LLD_A >= max(1,LOCp(M_A))	Local

Specified as: an array of (at least) length 9, containing fullword integers.

b

is the local part of the global general matrix B. This identifies the first element of the local array B. This subroutine computes the location of the first element of the local subarray used, based on ib, jb, desc_b, p, q, myrow, and mycol; therefore:

If trans = 'N', the leading LOCp(ib+n-1) by LOCq(jb+k-1) part of the local array B must contain the local pieces of the leading ib+n-1 by jb+k-1 part of the global matrix.
If trans = 'T' or 'C', the leading LOCp(ib+k-1) by LOCq(jb+n-1) part of the local array B must contain the local pieces of the leading ib+k-1 by jb+n-1 part of the global matrix.

Note:: No data should be moved to form B^T or B^H; that is, the matrix B should always be stored in its untransposed form.

Scope: local

Specified as: an LLD_B by (at least) LOCq(N_B) array, containing numbers of the data type indicated in Table 52. Details about the block-cyclic data distribution of global matrix B are stored in desc_b.

ib

is the row index of the global matrix B, identifying the first row of the submatrix B.

Scope: global

Specified as: a fullword integer; 1 <= ib <= M_B, and:

If trans = 'N', then ib+n-1 <= M_B.

If trans = 'T' or 'C', then ib+k-1 <= M_B.

jb

is the column index of the global matrix B, identifying the first column of the submatrix B.

Scope: global

Specified as: a fullword integer; 1 <= jb <= N_B, and:

If trans = 'N', then jb+k-1 <= N_B.

If trans = 'T' or 'C', then jb+n-1 <= N_B.

desc_b

is the array descriptor for global matrix B, described in the following table:

`desc_b`	Name	Description	Limits	Scope
1	DTYPE_B	Descriptor type	DTYPE_B=1	Global
2	CTXT_B	BLACS context	Valid value, as returned by BLACS_GRIDINIT or BLACS_GRIDMAP	Global
3	M_B	Number of rows in the global matrix	If `n` = 0 or `k` = 0: M_B >= 0 Otherwise: M_B >= 1	Global
4	N_B	Number of columns in the global matrix	If `n` = 0 or `k` = 0: N_B >= 0 Otherwise: N_B >= 1	Global
5	MB_B	Row block size	MB_B >= 1	Global
6	NB_B	Column block size	NB_B >= 1	Global
7	RSRC_B	The process row of the `p` × `q` grid over which the first row of the global matrix is distributed	0 <= RSRC_B < `p`	Global
8	CSRC_B	The process column of the `p` × `q` grid over which the first column of the global matrix is distributed	0 <= CSRC_B < `q`	Global
9	LLD_B	The leading dimension of the local array	LLD_B >= max(1,LOCp(M_B))	Local

Specified as: an array of (at least) length 9, containing fullword integers.

beta

is the scalar beta.

Scope: global

Specified as: a number of the data type indicated in Table 52.

c

is the local part of the global real symmetric, complex symmetric, or complex Hermitian matrix C. This identifies the first element of the local array C. This subroutine computes the location of the first element of the local subarray used, based on ic, jc, desc_c, p, q, myrow, and mycol; therefore, the leading LOCp(ic+n-1) by LOCq(jc+n-1) part of the local array C must contain the local pieces of the leading ic+n-1 by jc+n-1 part of the global matrix, and:

If uplo = 'U', the leading n × n upper triangular part of the global submatrix C_{ic:ic+n-1,
jc:jc+n-1} must contain the upper triangular part of the submatrix, and the strictly lower triangular part is not referenced.
If uplo = 'L', the leading n × n lower triangular part of the global submatrix C_{ic:ic+n-1,
jc:jc+n-1} must contain the lower triangular part of the submatrix, and the strictly upper triangular part is not referenced.

When beta is zero, C need not be set on input.

Scope: local

Specified as: an LLD_C by (at least) LOCq(N_C) array, containing numbers of the data type indicated in Table 52. Details about the block-cyclic data distribution of global matrix C are stored in desc_c.

ic

is the row index of the global matrix C, identifying the first row of the submatrix C.

Scope: global

Specified as: a fullword integer; 1 <= ic <= M_C and ic+n-1 <= M_C.

jc

is the column index of the global matrix C, identifying the first column of the submatrix C.

Scope: global

Specified as: a fullword integer; 1 <= jc <= N_C and jc+n-1 <= N_C.

desc_c

is the array descriptor for global matrix C, described in the following table:

`desc_c`	Name	Description	Limits	Scope
1	DTYPE_C	Descriptor type	DTYPE_C=1	Global
2	CTXT_C	BLACS context	Valid value, as returned by BLACS_GRIDINIT or BLACS_GRIDMAP	Global
3	M_C	Number of rows in the global matrix	If `n` = 0: M_C >= 0 Otherwise: M_C >= 1	Global
4	N_C	Number of columns in the global matrix	If `n` = 0: N_C >= 0 Otherwise: N_C >= 1	Global
5	MB_C	Row block size	MB_C >= 1	Global
6	NB_C	Column block size	NB_C >= 1	Global
7	RSRC_C	The process row of the `p` × `q` grid over which the first row of the global matrix is distributed	0 <= RSRC_C < `p`	Global
8	CSRC_C	The process column of the `p` × `q` grid over which the first column of the global matrix is distributed	0 <= CSRC_C < `q`	Global
9	LLD_C	The leading dimension of the local array	LLD_C >= max(1,LOCp(M_C))	Local

Specified as: an array of (at least) length 9, containing fullword integers.

On Return

c

is the updated local part of the global real symmetric, complex symmetric, or complex Hermitian matrix C, containing the results of the computation.

Scope: local

Returned as: an LLD_C by (at least) LOCq(N_C) array, containing numbers of the data type indicated in Table 52.

Notes and Coding Rules

These subroutines accept lowercase letters for the uplo and trans arguments.
For PDSYR2K, if you specify 'C' for the trans argument, it is interpreted as though you specified 'T'.
The imaginary parts of the diagonal elements of a complex Hermitian matrix C are assumed to be zero, so you do not have to set these values. On output, they are set to zero, except when beta is one and alpha or k is zero, in which case no computation is performed.
The matrices must have no common elements; otherwise, results are unpredictable.
The NUMROC utility subroutine can be used to determine the values of LOCp(M_) and LOCq(N_) used in the argument descriptions above. For details, see Determining the Number of Rows and Columns in Your Local Arrays and NUMROC--Compute the Number of Rows or Columns of a Block-Cyclically Distributed Matrix Contained in a Process.
For suggested block sizes, see Coding Tips for Optimizing Parallel Performance.
The following values must be equal: CTXT_A = CTXT_B = CTXT_C.
If trans = 'N':
- In the process grid, the process row containing the first row of the submatrix C must also contain the first row of the submatrices A and B; that is:
  
  icrow = iarow
  icrow = ibrow
  where:
  
  iarow = mod((((ia-1)/MB_A)+RSRC_A), p)
  ibrow = mod((((ib-1)/MB_B)+RSRC_B), p)
  icrow = mod((((ic-1)/MB_C)+RSRC_C), p)
- If looping is required--that is, either of the following is true:
  
  k+mod(ja-1, NB_A) > NB_A
  k+mod(jb-1, NB_B) > NB_B
  
  then the block column offset of A must be equal to the block column offset of B; that is, mod(ja-1, NB_A) = mod(jb-1, NB_B).
If trans = 'T' or 'C':
- In the process grid, the process column containing the first column of the submatrix C must also contain the first column of the submatrices A and B; that is:
  
  iccol = iacol
  iccol = ibcol
  where:
  
  iacol = mod((((ja-1)/NB_A)+CSRC_A), q)
  ibcol = mod((((jb-1)/NB_B)+CSRC_B), q)
  iccol = mod((((jc-1)/NB_C)+CSRC_C), q)
- If looping is required--that is, either of the following is true:
  
  k+mod(ia-1, MB_A) > MB_A
  k+mod(ib-1, MB_B) > MB_B
  
  then the block row offset of A must be equal to the block row offset of B; that is, mod(ia-1, MB_A) = mod(ib-1, MB_B)
If all the following are true:
- C is contained within a single block, that is:
  
  n+mod(ic-1, MB_C) <= MB_C
  n+mod(jc-1, NB_C) <= NB_C
- If trans = 'N', then (in the process grid) the process column containing the first column of the submatrix A must also contain the first column of the submatrix B; that is, iacol = ibcol, where:
  
  iacol = mod((((ja-1)/NB_A)+CSRC_A), q)
  ibcol = mod((((jb-1)/NB_B)+CSRC_B), q)
- If trans = 'T' or 'C', then (in the process grid) the process row containing the first row of the submatrix A must also contain the first row of the submatrix B; that is, iarow = ibrow, where:
  
  iarow = mod((((ia-1)/MB_A)+RSRC_A), p)
  ibrow = mod((((ib-1)/MB_B)+RSRC_B), p)
then you must follow these rules:
- If trans = 'N':
  - A and B must be block row matrices; that is, if p > 1:
    
    n+mod(ia-1, MB_A) <= MB_A
    n+mod(ib-1, MB_B) <= MB_B
  - If looping is required, the following block sizes must be equal: NB_A = NB_B.
- If trans = 'T' or 'C':
  - A and B must be block column matrices; that is, if q > 1:
    
    n+mod(ja-1, NB_A) <= NB_A
    n+mod(jb-1, NB_B) <= NB_B
  - If looping is required, the following block sizes must be equal: MB_A = MB_B.
If the following is true:
- C is not contained within a single block.
or if all the following are true:
- C is contained within a single block.
- If trans = 'N', then (in the process grid) the process column containing the first column of the submatrix A does not contain the first column of the submatrix B; that is, iacol <> ibcol, where:
  
  iacol = mod((((ja-1)/NB_A)+CSRC_A), q)
  ibcol = mod((((jb-1)/NB_B)+CSRC_B), q)
- If trans = 'T' or 'C', then (in the process grid) the process row containing the first row of the submatrix A does not contain the first row of the submatrix B; that is, iarow <> ibrow, where:
  
  iarow = mod((((ia-1)/MB_A)+RSRC_A), p)
  ibrow = mod((((ib-1)/MB_B)+RSRC_B), p)
then you must follow these rules:
- The global symmetric matrix C must be distributed using a square block-cyclic distribution; that is, MB_C = NB_C.
- The global symmetric matrix C must be aligned on a block boundary, that is:
  
  ic-1 must be a multiple of MB_C.
  jc-1 must be a multiple of NB_C.
- If trans = 'N':
  - The following block sizes must be equal:
    
    NB_A = NB_B
    MB_A = MB_B = NB_C.
  - The global matrices A and B must be aligned on a block row boundary, that is:
    
    ia-1 must be a multiple of MB_A.
    ib-1 must be a multiple of MB_B.
- If trans = 'T' or 'C':
  - The following block sizes must be equal:
    
    MB_A = MB_B
    NB_A = NB_B = MB_C.
  - The global matrices A and B must be aligned on a block column boundary, that is:
    
    ja-1 must be a multiple of NB_A.
    jb-1 must be a multiple of NB_B.

DTYPE_A is invalid.
DTYPE_B is invalid.
DTYPE_C is invalid.

Stage 2:

CTXT_A is invalid.

Stage 3:

This subroutine was called from outside the process grid.

Stage 4:

uplo <> 'U' or 'L'
trans <>
- 'N', 'T', or 'C' for PDSYR2K
- 'N' or 'T' for PZSYR2K
- 'N' or 'C' for PZHER2K
n < 0 and trans = 'N'; n < 0 and trans = 'T' or 'C'; n < 0 and trans is invalid.
k < 0 and trans = 'N'; k < 0 and trans = 'T' or 'C'; k < 0 and trans is invalid.
M_A < 0 and (n = 0 or k = 0); M_A < 1 otherwise
N_A < 0 and (n = 0 or k = 0); N_A < 1 otherwise
MB_A < 1
NB_A < 1
RSRC_A < 0 or RSRC_A >= p
CSRC_A < 0 or CSRC_A >= q
ia < 1
ja < 1
M_B < 0 and (n = 0 or k = 0); M_B < 1 otherwise
N_B < 0 and (n = 0 or k = 0); N_B < 1 otherwise
MB_B < 1
NB_B < 1
RSRC_B < 0 or RSRC_B >= p
CSRC_B < 0 or CSRC_B >= q
ib < 1
jb < 1
M_C < 0 and n = 0; M_C < 1 otherwise
N_C < 0 and n = 0; N_C < 1 otherwise
MB_C < 1
NB_C < 1
RSRC_C < 0 or RSRC_C >= p
CSRC_C < 0 or CSRC_C >= q
ic < 1
jc < 1
CTXT_A <> CTXT_B
CTXT_A <> CTXT_C

Stage 5: If n <> 0 and k <> 0:

ia > M_A
ja > N_A
trans = 'N' and ia+n-1 > M_A
trans = 'N' and ja+k-1 > N_A
trans = 'T' or 'C' and ia+k-1 > M_A
trans = 'T' or 'C' and ja+n-1 > N_A
ib > M_B
jb > N_B
trans = 'N' and ib+n-1 > M_B
trans = 'N' and jb+k-1 > N_B
trans = 'T' or 'C' and ib+k-1 > M_B
trans = 'T' or 'C' and jb+n-1 > N_B

If n <> 0:
ic > M_C
jc > N_C
ic+n-1 > M_C
jc+n-1 > N_C

Stage 6: If C is contained within a single block, that is:

n+mod(ic-1, MB_C) <= MB_C

n+mod(jc-1, NB_C) <= NB_C

and:

If trans = 'N', then (in the process grid) the process column containing the first column of the submatrix A must also contain the first column of the submatrix B; that is, iacol = ibcol, where:

iacol = mod((((ja-1)/NB_A)+CSRC_A), q)
ibcol = mod((((jb-1)/NB_B)+CSRC_B), q)
If trans = 'T' or 'C', then (in the process grid) the process row containing the first row of the submatrix A must also contain the first row of the submatrix B; that is, iarow = ibrow, where:

iarow = mod((((ia-1)/MB_A)+RSRC_A), p)
ibrow = mod((((ib-1)/MB_B)+RSRC_B), p)

then:

If trans = 'N':
1. p > 1 and n+mod(ia-1, MB_A) > MB_A
2. p > 1 and n+mod(ib-1, MB_B) > MB_B
3. Looping is required--that is, either of the following is true:
  
  k+mod(ja-1, NB_A) > NB_A
  k+mod(jb-1, NB_B) > NB_B
  
  and NB_A <> NB_B.
If trans = 'T' or 'C':
1. q > 1 and n+mod(ja-1, NB_A) > NB_A
2. q > 1 and n+mod(jb-1, NB_B) > NB_B
3. Looping is required--that is, either of the following is true:
  
  k+mod(ia-1, MB_A) > MB_A
  k+mod(ib-1, MB_B) > MB_B
  
  and MB_A <> MB_B.

If C is not contained within a single block, or if C is contained within a single block and:

If trans = 'N', then (in the process grid) the process column containing the first column of the submatrix A does not contain the first column of the submatrix B; that is, iacol <> ibcol, where:

iacol = mod((((ja-1)/NB_A)+CSRC_A), q)
ibcol = mod((((jb-1)/NB_B)+CSRC_B), q)
If trans = 'T' or 'C', then (in the process grid) the process row containing the first row of the submatrix A does not contain the first row of the submatrix B; that is, iarow <> ibrow, where:

iarow = mod((((ia-1)/MB_A)+RSRC_A), p)
ibrow = mod((((ib-1)/MB_B)+RSRC_B), p)

then:

MB_C <> NB_C
mod(ic-1, MB_C) <> 0
mod(jc-1, NB_C) <> 0

If trans = 'N':
NB_C <> MB_A
NB_C <> MB_B
NB_A <> NB_B
mod(ia-1, MB_A) <> 0
mod(ib-1, MB_B) <> 0

If trans = 'T' or 'C':
MB_C <> NB_A
MB_C <> NB_B
MB_A <> MB_B
mod(ja-1, NB_A) <> 0
mod(jb-1, NB_B) <> 0

In all cases:

LLD_A < max(1, LOCp(M_A))
LLD_B < max(1, LOCp(M_B))
LLD_C < max(1, LOCp(M_C))

If trans = 'N':
Looping is required and mod(ja-1, NB_A) <> mod(jb-1, NB_B).
In the process grid, the process row containing the first row of the submatrix C does not contain the first row of the submatrix A; that is, icrow <> iarow, where:

icrow = mod((((ic-1)/MB_C)+RSRC_C), p)
iarow = mod((((ia-1)/MB_A)+RSRC_A), p)
In the process grid, the process row containing the first row of the submatrix C does not contain the first row of the submatrix B; that is, icrow <> ibrow, where:

icrow = mod((((ic-1)/MB_C)+RSRC_C), p)
ibrow = mod((((ib-1)/MB_B)+RSRC_B), p)

If trans = 'T' or 'C':
Looping is required and mod(ia-1, MB_A) <> mod(ib-1, MB_B).
In the process grid, the process column containing the first column of the submatrix C does not contain the first column of the submatrix A; that is, iccol <> iacol, where:

iccol = mod((((jc-1)/NB_C)+CSRC_C), q)
iacol = mod((((ja-1)/NB_A)+CSRC_A), q)
In the process grid, the process column containing the first column of the submatrix C does not contain the first column of the submatrix B; that is, iccol <> ibcol, where:

iccol = mod((((jc-1)/NB_C)+CSRC_C), q)
ibcol = mod((((jb-1)/NB_B)+CSRC_B), q)

Example 1

This example computes C = alphaA^TB+alphaB^TA+betaC using a 2 × 2 process grid.

Call Statements and Input

 ORDER = 'R'
 NPROW = 2
 NPCOL = 2
 CALL BLACS_GET (0, 0, ICONTXT)
 CALL BLACS_GRIDINIT(ICONTXT, ORDER, NPROW, NPCOL)
 CALL BLACS_GRIDINFO(ICONTXT, NPROW, NPCOL, MYROW, MYCOL)
 
              UPLO   TRANS   N    K     ALPHA    A  IA  JA    DESC_A   B  IB  JB
                |      |     |    |       |      |   |   |      |      |   |   |
 CALL PDSYR2K( 'U' ,  'T' ,  9  , 8  ,  1.0D0  , A , 1 , 1 ,  DESC_A , B , 1 , 1 ,
 
               DESC_B    BETA    C  IC  JC   DESC_C
                 |         |     |   |   |     |
               DESC_B ,  0.0D0 , C , 1 , 1 , DESC_C )

	Desc_A	Desc_B	Desc_C
DTYPE_	1	1	1
CTXT_	`icontxt`^(IOBG29)	`icontxt`^(IOBG29)	`icontxt`^(IOBG29)
M_	8	8	9
N_	9	9	9
MB_	2	2	4
NB_	4	4	4
RSRC_	0	0	0
CSRC_	0	0	0
LLD_	See below^(EPSSL29)	See below^(EPSSL29)	See below^(EPSSL29)
Notes: `icontxt` is the output of the BLACS_GRIDINIT call. Each process should set the LLD_ as follows: LLD_A = MAX(1,NUMROC(M_A, MB_A, MYROW, RSRC_A, NPROW)) LLD_B = MAX(1,NUMROC(M_B, MB_B, MYROW, RSRC_B, NPROW)) LLD_C = MAX(1,NUMROC(M_C, MB_C, MYROW, RSRC_C, NPROW)) In this example, LLD_A = LLD_B = 4 on all processes, LLD_C = 5 on P₀₀ and P₀₁, and LLD_C = 4 on P₁₀ and P₁₁.

Global general 8 × 9 matrix A with block size 2 × 4:

B,D             0                       1               2
     *                                                      *
 0   |  0.0 -1.0 -1.0  0.0  |   0.0  0.0  0.0  0.0  |   1.0 |
     |  0.0  1.0  0.0  1.0  |   0.0  1.0  0.0  1.0  |   1.0 |
     | ---------------------|-----------------------|------ |
 1   |  0.0  0.0 -1.0 -1.0  |   0.0  0.0  1.0  0.0  |   1.0 |
     |  0.0  1.0  0.0 -1.0  |   1.0  1.0  0.0  1.0  |   1.0 |
     | ---------------------|-----------------------|------ |
 2   |  1.0  0.0  0.0  0.0  |  -1.0  0.0  0.0  0.0  |   1.0 |
     |  1.0  0.0  0.0  0.0  |   1.0  1.0  0.0  0.0  |   1.0 |
     | ---------------------|-----------------------|------ |
 3   |  0.0  0.0 -1.0  0.0  |  -1.0  0.0  0.0  0.0  |   1.0 |
     | -1.0  0.0  0.0  0.0  |   0.0  0.0 -1.0  0.0  |   1.0 |
     *                                                      *

The following is the 2 × 2 process grid:

B,D  |  0 2  | 1 
-----|-------|-----
0    |   P₀₀   |  P₀₁
2    |       |
-----|-------|-----
1    |   P₁₀   |  P₁₁
3    |       |

Local arrays for A:

p,q  |            0              |           1
-----|---------------------------|----------------------
     |  0.0 -1.0 -1.0  0.0  1.0  |   0.0  0.0  0.0  0.0
     |  0.0  1.0  0.0  1.0  1.0  |   0.0  1.0  0.0  1.0
 0   |  1.0  0.0  0.0  0.0  1.0  |  -1.0  0.0  0.0  0.0
     |  1.0  0.0  0.0  0.0  1.0  |   1.0  1.0  0.0  0.0
-----|---------------------------|----------------------
     |  0.0  0.0 -1.0 -1.0  1.0  |   0.0  0.0  1.0  0.0
     |  0.0  1.0  0.0 -1.0  1.0  |   1.0  1.0  0.0  1.0
 1   |  0.0  0.0 -1.0  0.0  1.0  |  -1.0  0.0  0.0  0.0
     | -1.0  0.0  0.0  0.0  1.0  |   0.0  0.0 -1.0  0.0

Global general 8 × 9 matrix B with block size 2 × 4:

B,D             0                       1               2
     *                                                      *
 0   |  0.0  1.0  1.0  0.0  |   0.0  0.0  0.0  0.0  |  -1.0 |
     |  0.0 -1.0  0.0 -1.0  |   0.0 -1.0  0.0 -1.0  |  -1.0 |
     | ---------------------|-----------------------|------ |
 1   |  0.0  0.0  1.0  1.0  |   0.0  0.0 -1.0  0.0  |  -1.0 |
     |  0.0 -1.0  0.0  1.0  |  -1.0 -1.0  0.0 -1.0  |  -1.0 |
     | ---------------------|-----------------------|------ |
 2   | -1.0  0.0  0.0  0.0  |   1.0  0.0  0.0  0.0  |  -1.0 |
     | -1.0  0.0  0.0  0.0  |  -1.0 -1.0  0.0  0.0  |  -1.0 |
     | ---------------------|-----------------------|------ |
 3   |  0.0  0.0  1.0  0.0  |   1.0  0.0  0.0  0.0  |  -1.0 |
     |  1.0  0.0  0.0  0.0  |   0.0  0.0  1.0  0.0  |  -1.0 |
     *                                                      *

The following is the 2 × 2 process grid:

B,D  |  0 2  | 1 
-----|-------|-----
0    |   P₀₀   |  P₀₁
2    |       |
-----|-------|-----
1    |   P₁₀   |  P₁₁
3    |       |

Local arrays for B:

p,q  |            0              |           1
-----|---------------------------|----------------------
     |  0.0  1.0  1.0  0.0 -1.0  |   0.0  0.0  0.0  0.0
     |  0.0 -1.0  0.0 -1.0 -1.0  |   0.0 -1.0  0.0 -1.0
 0   | -1.0  0.0  0.0  0.0 -1.0  |   1.0  0.0  0.0  0.0
     | -1.0  0.0  0.0  0.0 -1.0  |  -1.0 -1.0  0.0  0.0
-----|---------------------------|----------------------
     |  0.0  0.0  1.0  1.0 -1.0  |   0.0  0.0 -1.0  0.0
     |  0.0 -1.0  0.0  1.0 -1.0  |  -1.0 -1.0  0.0 -1.0
 1   |  0.0  0.0  1.0  0.0 -1.0  |   1.0  0.0  0.0  0.0
     |  1.0  0.0  0.0  0.0 -1.0  |   0.0  0.0  1.0  0.0

Output:

Global real symmetric matrix C of order 9 with block size 4 × 4:

B,D             0                       1                2
     *                                                       *
     | -6.0  0.0  0.0  0.0  |   0.0 -2.0 -2.0  0.0  |  -2.0  |
     |   .  -6.0 -2.0  0.0  |  -2.0 -4.0  0.0 -4.0  |  -2.0  |
 0   |   .    .  -6.0 -2.0  |  -2.0  0.0  2.0  0.0  |   6.0  |
     |   .    .    .  -6.0  |   2.0  0.0  2.0  0.0  |   2.0  |
     | ---------------------|-----------------------|------- |
     |   .    .    .    .   |  -8.0 -4.0  0.0 -2.0  |   0.0  |
     |   .    .    .    .   |    .  -6.0  0.0 -4.0  |  -6.0  |
 1   |   .    .    .    .   |    .    .  -4.0  0.0  |   0.0  |
     |   .    .    .    .   |    .    .    .  -4.0  |  -4.0  |
     | ---------------------|-----------------------|------- |
 2   |   .    .    .    .   |    .    .    .    .   |  -16.0 |
     *                                                       *

The following is the 2 × 2 process grid:

B,D  |  0 2  | 1 
-----|-------|-----
0    |   P₀₀   |  P₀₁
2    |       |
-----|-------|-----
1    |   P₁₀   |  P₁₁

Local arrays for C:

p,q  |             0              |           1
-----|----------------------------|----------------------
     | -6.0  0.0  0.0  0.0  -2.0  |   0.0 -2.0 -2.0  0.0
     |   .  -6.0 -2.0  0.0  -2.0  |  -2.0 -4.0  0.0 -4.0
 0   |   .    .  -6.0 -2.0   6.0  |  -2.0  0.0  2.0  0.0
     |   .    .    .  -6.0   2.0  |   2.0  0.0  2.0  0.0
     |   .    .    .    .  -16.0  |    .    .    .    .
-----|----------------------------|----------------------
     |   .    .    .    .    0.0  |  -8.0 -4.0  0.0 -2.0
     |   .    .    .    .   -6.0  |    .  -6.0  0.0 -4.0
 1   |   .    .    .    .    0.0  |    .    .  -4.0  0.0
     |   .    .    .    .   -4.0  |    .    .    .  -4.0

Example 2

This example computes C = alphaA^TB+alphaB^TA+betaC using a 2 × 2 process grid.

Call Statements and Input

 ORDER = 'R'
 NPROW = 2
 NPCOL = 2
 CALL BLACS_GET (0, 0, ICONTXT)
 CALL BLACS_GRIDINIT(ICONTXT, ORDER, NPROW, NPCOL)
 CALL BLACS_GRIDINFO(ICONTXT, NPROW, NPCOL, MYROW, MYCOL)
 
              UPLO   TRANS   N    K     ALPHA    A  IA  JA    DESC_A   B  IB  JB
                |      |     |    |       |      |   |   |      |      |   |   |
 CALL PZSYR2K( 'U' ,  'T' ,  7  , 8  ,  ALPHA  , A , 1 , 1 ,  DESC_A , B , 1 , 1 ,
 
               DESC_B    BETA    C  IC  JC   DESC_C
                 |         |     |   |   |     |
               DESC_B ,  BETA  , C , 1 , 1 , DESC_C )
 
               ALPHA = (1.0,0.0)
 
               BETA  = (0.0,0.0)

	Desc_A	Desc_B	Desc_C
DTYPE_	1	1	1
CTXT_	`icontxt`^(IOBG30)	`icontxt`^(IOBG30)	`icontxt`^(IOBG30)
M_	8	8	7
N_	7	7	7
MB_	2	2	3
NB_	3	3	3
RSRC_	0	0	0
CSRC_	0	0	0
LLD_	See below^(EPSSL30)	See below^(EPSSL30)	See below^(EPSSL30)
Notes: `icontxt` is the output of the BLACS_GRIDINIT call. Each process should set the LLD_ as follows: LLD_A = MAX(1,NUMROC(M_A, MB_A, MYROW, RSRC_A, NPROW)) LLD_B = MAX(1,NUMROC(M_B, MB_B, MYROW, RSRC_B, NPROW)) LLD_C = MAX(1,NUMROC(M_C, MB_C, MYROW, RSRC_C, NPROW)) In this example, LLD_A = LLD_B = 4 on all processes, LLD_C = 4 on P₀₀ and P₀₁, and LLD_C = 3 on P₁₀ and P₁₁.

Global general 8 × 7 matrix A with block size 2 × 3:

B,D                     0                                     1                          2
     *                                                                                          *
 0   | ( 0.0, 1.0) (-1.0, 0.0) (-1.0, 0.0) | ( 0.0, 1.0) ( 0.0, 1.0) ( 0.0, 1.0)  | ( 0.0, 1.0) |
     | ( 0.0, 1.0) ( 1.0, 2.0) ( 0.0, 1.0) | ( 1.0, 2.0) ( 0.0, 1.0) ( 1.0, 2.0)  | ( 0.0, 1.0) |
     | ------------------------------------|--------------------------------------|------------ |
 1   | ( 0.0, 1.0) ( 0.0, 1.0) (-1.0, 0.0) | (-1.0, 0.0) ( 0.0, 1.0) ( 0.0, 1.0)  | ( 1.0, 2.0) |
     | ( 0.0, 1.0) ( 1.0, 2.0) ( 0.0, 1.0) | (-1.0, 0.0) ( 1.0, 2.0) ( 1.0, 2.0)  | ( 0.0, 1.0) |
     | ------------------------------------|--------------------------------------|------------ |
 2   | ( 1.0, 2.0) ( 0.0, 1.0) ( 0.0, 1.0) | ( 0.0, 1.0) (-1.0, 0.0) ( 0.0, 1.0)  | ( 0.0, 1.0) |
     | ( 1.0, 2.0) ( 0.0, 1.0) ( 0.0, 1.0) | ( 0.0, 1.0) ( 1.0, 2.0) ( 1.0, 2.0)  | ( 0.0, 1.0) |
     | ------------------------------------|--------------------------------------|------------ |
 3   | ( 0.0, 1.0) ( 0.0, 1.0) (-1.0, 0.0) | ( 0.0, 1.0) (-1.0, 0.0) ( 0.0, 1.0)  | ( 0.0, 1.0) |
     | (-1.0, 0.0) ( 0.0, 1.0) ( 0.0, 1.0) | ( 0.0, 1.0) ( 0.0, 1.0) ( 0.0, 1.0)  | (-1.0, 0.0) |
     *                                                                                          *

The following is the 2 × 2 process grid:

B,D  |  0 2  | 1 
-----|-------|-----
0    |   P₀₀   |  P₀₁
2    |       |
-----|-------|-----
1    |   P₁₀   |  P₁₁
3    |       |

Local arrays for A:

p,q  |                        0                        |                  1
-----|-------------------------------------------------|-------------------------------------
     | ( 0.0, 1.0) (-1.0, 0.0) (-1.0, 0.0) ( 0.0, 1.0) | ( 0.0, 1.0) ( 0.0, 1.0) ( 0.0, 1.0)
     | ( 0.0, 1.0) ( 1.0, 2.0) ( 0.0, 1.0) ( 0.0, 1.0) | ( 1.0, 2.0) ( 0.0, 1.0) ( 1.0, 2.0)
 0   | ( 1.0, 2.0) ( 0.0, 1.0) ( 0.0, 1.0) ( 0.0, 1.0) | ( 0.0, 1.0) (-1.0, 0.0) ( 0.0, 1.0)
     | ( 1.0, 2.0) ( 0.0, 1.0) ( 0.0, 1.0) ( 0.0, 1.0) | ( 0.0, 1.0) ( 1.0, 2.0) ( 1.0, 2.0)
-----|-------------------------------------------------|-------------------------------------
     | ( 0.0, 1.0) ( 0.0, 1.0) (-1.0, 0.0) ( 1.0, 2.0) | (-1.0, 0.0) ( 0.0, 1.0) ( 0.0, 1.0)
     | ( 0.0, 1.0) ( 1.0, 2.0) ( 0.0, 1.0) ( 0.0, 1.0) | (-1.0, 0.0) ( 1.0, 2.0) ( 1.0, 2.0)
 1   | ( 0.0, 1.0) ( 0.0, 1.0) (-1.0, 0.0) ( 0.0, 1.0) | ( 0.0, 1.0) (-1.0, 0.0) ( 0.0, 1.0)
     | (-1.0, 0.0) ( 0.0, 1.0) ( 0.0, 1.0) (-1.0, 0.0) | ( 0.0, 1.0) ( 0.0, 1.0) ( 0.0, 1.0)

Global general 8 × 7 matrix B with block size 2 × 3:

B,D                     0                                     1                          2
     *                                                                                          *
 0   | ( 0.0,-2.0) ( 1.0,-1.0) ( 1.0,-1.0) | ( 0.0,-2.0) ( 0.0,-2.0) ( 0.0,-2.0)  | ( 0.0,-2.0) |
     | ( 0.0,-2.0) (-1.0,-3.0) ( 0.0,-2.0) | (-1.0,-3.0) ( 0.0,-2.0) (-1.0,-3.0)  | ( 0.0,-2.0) |
     | ------------------------------------|--------------------------------------|------------ |
 1   | ( 0.0,-2.0) ( 0.0,-2.0) ( 1.0,-1.0) | ( 1.0,-1.0) ( 0.0,-2.0) ( 0.0,-2.0)  | (-1.0,-3.0) |
     | ( 0.0,-2.0) (-1.0,-3.0) ( 0.0,-2.0) | ( 1.0,-1.0) (-1.0,-3.0) (-1.0,-3.0)  | ( 0.0,-2.0) |
     | ------------------------------------|--------------------------------------|------------ |
 2   | (-1.0,-3.0) ( 0.0,-2.0) ( 0.0,-2.0) | ( 0.0,-2.0) ( 1.0,-1.0) ( 0.0,-2.0)  | ( 0.0,-2.0) |
     | (-1.0,-3.0) ( 0.0,-2.0) ( 0.0,-2.0) | ( 0.0,-2.0) (-1.0,-3.0) (-1.0,-3.0)  | ( 0.0,-2.0) |
     | ------------------------------------|--------------------------------------|------------ |
 3   | ( 0.0,-2.0) ( 0.0,-2.0) ( 1.0,-1.0) | ( 0.0,-2.0) ( 1.0,-1.0) ( 0.0,-2.0)  | ( 0.0,-2.0) |
     | ( 1.0,-1.0) ( 0.0,-2.0) ( 0.0,-2.0) | ( 0.0,-2.0) ( 0.0,-2.0) ( 0.0,-2.0)  | ( 1.0,-1.0) |
     *                                                                                          *

The following is the 2 × 2 process grid:

B,D  |  0 2  | 1 
-----|-------|-----
0    |   P₀₀   |  P₀₁
2    |       |
-----|-------|-----
1    |   P₁₀   |  P₁₁
3    |       |

Local arrays for B:

p,q  |                        0                        |                  1
-----|-------------------------------------------------|-------------------------------------
     | ( 0.0,-2.0) ( 1.0,-1.0) ( 1.0,-1.0) ( 0.0,-2.0) | ( 0.0,-2.0) ( 0.0,-2.0) ( 0.0,-2.0)
     | ( 0.0,-2.0) (-1.0,-3.0) ( 0.0,-2.0) ( 0.0,-2.0) | (-1.0,-3.0) ( 0.0,-2.0) (-1.0,-3.0)
 0   | (-1.0,-3.0) ( 0.0,-2.0) ( 0.0,-2.0) ( 0.0,-2.0) | ( 0.0,-2.0) ( 1.0,-1.0) ( 0.0,-2.0)
     | (-1.0,-3.0) ( 0.0,-2.0) ( 0.0,-2.0) ( 0.0,-2.0) | ( 0.0,-2.0) (-1.0,-3.0) (-1.0,-3.0)
-----|-------------------------------------------------|-------------------------------------
     | ( 0.0,-2.0) ( 0.0,-2.0) ( 1.0,-1.0) (-1.0,-3.0) | ( 1.0,-1.0) ( 0.0,-2.0) ( 0.0,-2.0)
     | ( 0.0,-2.0) (-1.0,-3.0) ( 0.0,-2.0) ( 0.0,-2.0) | ( 1.0,-1.0) (-1.0,-3.0) (-1.0,-3.0)
 1   | ( 0.0,-2.0) ( 0.0,-2.0) ( 1.0,-1.0) ( 0.0,-2.0) | ( 0.0,-2.0) ( 1.0,-1.0) ( 0.0,-2.0)
     | ( 1.0,-1.0) ( 0.0,-2.0) ( 0.0,-2.0) ( 1.0,-1.0) | ( 0.0,-2.0) ( 0.0,-2.0) ( 0.0,-2.0)

Output:

Global complex symmetric matrix C of order 7 with block size 3 × 3:

B,D                        0                                           1                             2
     *                                                                                                       *
     | ( 38.0,-18.0) ( 38.0, -6.0) ( 26.0,  6.0) | ( 32.0,  0.0) ( 35.0, -3.0) ( 44.0,-16.0) | ( 35.0, -7.0) |
 0   |       .       ( 38.0,-18.0) ( 26.0,  2.0) | ( 32.0,  0.0) ( 35.0, -7.0) ( 44.0,-20.0) | ( 35.0, -3.0) |
     |       .             .       ( 14.0,  6.0) | ( 20.0,  8.0) ( 23.0,  5.0) ( 32.0,  0.0) | ( 23.0, 13.0) |
     | ------------------------------------------|-------------------------------------------|-------------- |
     |       .             .             .       | ( 26.0, -6.0) ( 29.0,  7.0) ( 38.0, -6.0) | ( 29.0,  7.0) |
 1   |       .             .             .       |       .       ( 32.0,-16.0) ( 41.0,-17.0) | ( 32.0,  0.0) |
     |       .             .             .       |       .             .       ( 50.0,-30.0) | ( 41.0, -9.0) |
     | ------------------------------------------|-------------------------------------------|-------------- |
 2   |       .             .             .       |       .             .             ,       | ( 32.0, -8.0) |
     *                                                                                                       *

The following is the 2 × 2 process grid:

B,D  |  0 2  | 1 
-----|-------|-----
0    |   P₀₀   |  P₀₁
2    |       |
-----|-------|-----
1    |   P₁₀   |  P₁₁

Local arrays for C:

p,q  |                             0                            |                     1
-----|----------------------------------------------------------|-------------------------------------------
     | ( 38.0, -18.0) ( 38.0, -6.0) ( 26.0,  6.0) ( 35.0, -7.0) | ( 32.0,  0.0) ( 35.0, -3.0) ( 44.0,-16.0)
     |       .        ( 38.0,-18.0) ( 26.0,  2.0) ( 35.0, -3.0) | ( 32.0,  0.0) ( 35.0, -7.0) ( 44.0,-20.0)
 0   |       .              .       ( 14.0,  6.0) ( 23.0, 13.0) | ( 20.0,  8.0) ( 23.0,  5.0) ( 32.0,  0.0)
     |       .              .             .       ( 32.0, -8.0) |       .             .             .      
-----|----------------------------------------------------------|-------------------------------------------
     |       .              .             .       ( 29.0,  7.0) | ( 26.0, -6.0) ( 29.0,  7.0) ( 38.0, -6.0)
 1   |       .              .             .       ( 32.0,  0.0) |       .       ( 32.0,-16.0) ( 41.0,-17.0)
     |       .              .             .       ( 41.0, -9.0) |       .             .       ( 50.0,-30.0)

Example 3

This example computes:

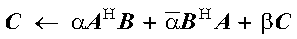
Rank-2K Update Graphic

using a 2 × 2 process grid.

Note:: The imaginary parts of the diagonal elements of a complex Hermitian matrix are assumed to be zero, so you do not have to set these values. On output, they are set to zero except when beta is one and alpha or k is zero.

Call Statements and Input

 ORDER = 'R'
 NPROW = 2
 NPCOL = 2
 CALL BLACS_GET (0, 0, ICONTXT)
 CALL BLACS_GRIDINIT(ICONTXT, ORDER, NPROW, NPCOL)
 CALL BLACS_GRIDINFO(ICONTXT, NPROW, NPCOL, MYROW, MYCOL)
 
              UPLO   TRANS   N    K     ALPHA    A  IA  JA    DESC_A   B  IB  JB
                |      |     |    |       |      |   |   |      |      |   |   |
 CALL PZHER2K( 'U' ,  'C' ,  7  , 8  ,  ALPHA  , A , 1 , 1 ,  DESC_A , B , 1 , 1 ,
 
               DESC_B    BETA    C  IC  JC   DESC_C
                 |         |     |   |   |     |
               DESC_B ,  BETA  , C , 1 , 1 , DESC_C )
 
               ALPHA = (1.0,0.0)
 
               BETA  = 0.0

	Desc_A	Desc_B	Desc_C
DTYPE_	1	1	1
CTXT_	`icontxt`^(IOBG31)	`icontxt`^(IOBG31)	`icontxt`^(IOBG31)
M_	8	8	7
N_	7	7	7
MB_	2	2	3
NB_	3	3	3
RSRC_	0	0	0
CSRC_	0	0	0
LLD_	See below^(EPSSL31)	See below^(EPSSL31)	See below^(EPSSL31)
Notes: `icontxt` is the output of the BLACS_GRIDINIT call. Each process should set the LLD_ as follows: LLD_A = MAX(1,NUMROC(M_A, MB_A, MYROW, RSRC_A, NPROW)) LLD_B = MAX(1,NUMROC(M_B, MB_B, MYROW, RSRC_B, NPROW)) LLD_C = MAX(1,NUMROC(M_C, MB_C, MYROW, RSRC_C, NPROW)) In this example, LLD_A = LLD_B = 4 on all processes, LLD_C = 4 on P₀₀ and P₀₁, and LLD_C = 3 on P₁₀ and P₁₁.

Global general 8 × 7 matrix A with block size 2 × 3:

B,D                     0                                     1                          2
     *                                                                                          *
 0   | ( 0.0, 1.0) (-1.0, 0.0) (-1.0, 0.0) | ( 0.0, 1.0) ( 0.0, 1.0) ( 0.0, 1.0)  | ( 0.0, 1.0) |
     | ( 0.0, 1.0) ( 1.0, 2.0) ( 0.0, 1.0) | ( 1.0, 2.0) ( 0.0, 1.0) ( 1.0, 2.0)  | ( 0.0, 1.0) |
     | ------------------------------------|--------------------------------------|------------ |
 1   | ( 0.0, 1.0) ( 0.0, 1.0) (-1.0, 0.0) | (-1.0, 0.0) ( 0.0, 1.0) ( 0.0, 1.0)  | ( 1.0, 2.0) |
     | ( 0.0, 1.0) ( 1.0, 2.0) ( 0.0, 1.0) | (-1.0, 0.0) ( 1.0, 2.0) ( 1.0, 2.0)  | ( 0.0, 1.0) |
     | ------------------------------------|--------------------------------------|------------ |
 2   | ( 1.0, 2.0) ( 0.0, 1.0) ( 0.0, 1.0) | ( 0.0, 1.0) (-1.0, 0.0) ( 0.0, 1.0)  | ( 0.0, 1.0) |
     | ( 1.0, 2.0) ( 0.0, 1.0) ( 0.0, 1.0) | ( 0.0, 1.0) ( 1.0, 2.0) ( 1.0, 2.0)  | ( 0.0, 1.0) |
     | ------------------------------------|--------------------------------------|------------ |
 3   | ( 0.0, 1.0) ( 0.0, 1.0) (-1.0, 0.0) | ( 0.0, 1.0) (-1.0, 0.0) ( 0.0, 1.0)  | ( 0.0, 1.0) |
     | (-1.0, 0.0) ( 0.0, 1.0) ( 0.0, 1.0) | ( 0.0, 1.0) ( 0.0, 1.0) ( 0.0, 1.0)  | (-1.0, 0.0) |
     *                                                                                          *

The following is the 2 × 2 process grid:

B,D  |  0 2  | 1 
-----|-------|-----
0    |   P₀₀   |  P₀₁
2    |       |
-----|-------|-----
1    |   P₁₀   |  P₁₁
3    |       |

Local arrays for A:

p,q  |                        0                        |                  1
-----|-------------------------------------------------|-------------------------------------
     | ( 0.0, 1.0) (-1.0, 0.0) (-1.0, 0.0) ( 0.0, 1.0) | ( 0.0, 1.0) ( 0.0, 1.0) ( 0.0, 1.0)
     | ( 0.0, 1.0) ( 1.0, 2.0) ( 0.0, 1.0) ( 0.0, 1.0) | ( 1.0, 2.0) ( 0.0, 1.0) ( 1.0, 2.0)
 0   | ( 1.0, 2.0) ( 0.0, 1.0) ( 0.0, 1.0) ( 0.0, 1.0) | ( 0.0, 1.0) (-1.0, 0.0) ( 0.0, 1.0)
     | ( 1.0, 2.0) ( 0.0, 1.0) ( 0.0, 1.0) ( 0.0, 1.0) | ( 0.0, 1.0) ( 1.0, 2.0) ( 1.0, 2.0)
-----|-------------------------------------------------|-------------------------------------
     | ( 0.0, 1.0) ( 0.0, 1.0) (-1.0, 0.0) ( 1.0, 2.0) | (-1.0, 0.0) ( 0.0, 1.0) ( 0.0, 1.0)
     | ( 0.0, 1.0) ( 1.0, 2.0) ( 0.0, 1.0) ( 0.0, 1.0) | (-1.0, 0.0) ( 1.0, 2.0) ( 1.0, 2.0)
 1   | ( 0.0, 1.0) ( 0.0, 1.0) (-1.0, 0.0) ( 0.0, 1.0) | ( 0.0, 1.0) (-1.0, 0.0) ( 0.0, 1.0)
     | (-1.0, 0.0) ( 0.0, 1.0) ( 0.0, 1.0) (-1.0, 0.0) | ( 0.0, 1.0) ( 0.0, 1.0) ( 0.0, 1.0)

Global general 8 × 7 matrix B with block size 2 × 3:

B,D                     0                                     1                          2
     *                                                                                          *
 0   | ( 0.0,-2.0) ( 1.0,-1.0) ( 1.0,-1.0) | ( 0.0,-2.0) ( 0.0,-2.0) ( 0.0,-2.0)  | ( 0.0,-2.0) |
     | ( 0.0,-2.0) (-1.0,-3.0) ( 0.0,-2.0) | (-1.0,-3.0) ( 0.0,-2.0) (-1.0,-3.0)  | ( 0.0,-2.0) |
     | ------------------------------------|--------------------------------------|------------ |
 1   | ( 0.0,-2.0) ( 0.0,-2.0) ( 1.0,-1.0) | ( 1.0,-1.0) ( 0.0,-2.0) ( 0.0,-2.0)  | (-1.0,-3.0) |
     | ( 0.0,-2.0) (-1.0,-3.0) ( 0.0,-2.0) | ( 1.0,-1.0) (-1.0,-3.0) (-1.0,-3.0)  | ( 0.0,-2.0) |
     | ------------------------------------|--------------------------------------|------------ |
 2   | (-1.0,-3.0) ( 0.0,-2.0) ( 0.0,-2.0) | ( 0.0,-2.0) ( 1.0,-1.0) ( 0.0,-2.0)  | ( 0.0,-2.0) |
     | (-1.0,-3.0) ( 0.0,-2.0) ( 0.0,-2.0) | ( 0.0,-2.0) (-1.0,-3.0) (-1.0,-3.0)  | ( 0.0,-2.0) |
     | ------------------------------------|--------------------------------------|------------ |
 3   | ( 0.0,-2.0) ( 0.0,-2.0) ( 1.0,-1.0) | ( 0.0,-2.0) ( 1.0,-1.0) ( 0.0,-2.0)  | ( 0.0,-2.0) |
     | ( 1.0,-1.0) ( 0.0,-2.0) ( 0.0,-2.0) | ( 0.0,-2.0) ( 0.0,-2.0) ( 0.0,-2.0)  | ( 1.0,-1.0) |
     *                                                                                          *

The following is the 2 × 2 process grid:

B,D  |  0 2  | 1 
-----|-------|-----
0    |   P₀₀   |  P₀₁
2    |       |
-----|-------|-----
1    |   P₁₀   |  P₁₁
3    |       |

Local arrays for B:

p,q  |                        0                        |                  1
-----|-------------------------------------------------|-------------------------------------
     | ( 0.0,-2.0) ( 1.0,-1.0) ( 1.0,-1.0) ( 0.0,-2.0) | ( 0.0,-2.0) ( 0.0,-2.0) ( 0.0,-2.0)
     | ( 0.0,-2.0) (-1.0,-3.0) ( 0.0,-2.0) ( 0.0,-2.0) | (-1.0,-3.0) ( 0.0,-2.0) (-1.0,-3.0)
 0   | (-1.0,-3.0) ( 0.0,-2.0) ( 0.0,-2.0) ( 0.0,-2.0) | ( 0.0,-2.0) ( 1.0,-1.0) ( 0.0,-2.0)
     | (-1.0,-3.0) ( 0.0,-2.0) ( 0.0,-2.0) ( 0.0,-2.0) | ( 0.0,-2.0) (-1.0,-3.0) (-1.0,-3.0)
-----|-------------------------------------------------|-------------------------------------
     | ( 0.0,-2.0) ( 0.0,-2.0) ( 1.0,-1.0) (-1.0,-3.0) | ( 1.0,-1.0) ( 0.0,-2.0) ( 0.0,-2.0)
     | ( 0.0,-2.0) (-1.0,-3.0) ( 0.0,-2.0) ( 0.0,-2.0) | ( 1.0,-1.0) (-1.0,-3.0) (-1.0,-3.0)
 1   | ( 0.0,-2.0) ( 0.0,-2.0) ( 1.0,-1.0) ( 0.0,-2.0) | ( 0.0,-2.0) ( 1.0,-1.0) ( 0.0,-2.0)
     | ( 1.0,-1.0) ( 0.0,-2.0) ( 0.0,-2.0) ( 1.0,-1.0) | ( 0.0,-2.0) ( 0.0,-2.0) ( 0.0,-2.0)

Output:

Global complex Hermitian matrix C of order 7 with block size 3 × 3:

B,D                        0                                           1                             2
     *                                                                                                       *
     | (-50.0,  0.0) (-38.0,  0.0) (-26.0,-12.0) | (-32.0, -6.0) (-35.0, -3.0) (-48.0,  6.0) | (-39.0, -3.0) |
 0   |       .       (-50.0,  0.0) (-30.0,-12.0) | (-32.0, -6.0) (-39.0, -3.0) (-52.0,  6.0) | (-35.0, -3.0) |
     |       .             .       (-26.0,  0.0) | (-24.0,  6.0) (-27.0,  9.0) (-32.0, 18.0) | (-19.0,  9.0) |
     | ------------------------------------------|-------------------------------------------|-------------- |
     |       .             .             .       | (-38.0,  0.0) (-25.0,  3.0) (-38.0, 12.0) | (-25.0,  3.0) |
 1   |       .             .             .       |       .       (-48.0,  0.0) (-49.0,  9.0) | (-32.0,  0.0) |
     |       .             .             .       |       .             .       (-62.0,  0.0) | (-41.0, -9.0) |
     | ------------------------------------------|-------------------------------------------|-------------- |
 2   |       .             .             .       |       .             .             ,       | (-40.0,  0.0) |
     *                                                                                                       *

The following is the 2 × 2 process grid:

B,D  |  0 2  | 1 
-----|-------|-----
0    |   P₀₀   |  P₀₁
2    |       |
-----|-------|-----
1    |   P₁₀   |  P₁₁

Local arrays for C:

p,q  |                             0                            |                     1
-----|----------------------------------------------------------|-------------------------------------------
     | (-50.0,   0.0) (-38.0,  0.0) (-26.0,-12.0) (-39.0, -3.0) | (-32.0, -6.0) (-35.0, -3.0) (-48.0,  6.0)
     |       .        (-50.0,  0.0) (-30.0,-12.0) (-35.0, -3.0) | (-32.0, -6.0) (-39.0, -3.0) (-52.0,  6.0)
 0   |       .              .       (-26.0,  0.0) (-19.0,  9.0) | (-24.0,  6.0) (-27.0,  9.0) (-32.0, 18.0)
     |       .              .             .       (-40.0,  0.0) |       .             .             .      
-----|----------------------------------------------------------|-------------------------------------------
     |       .              .             .       (-25.0,  3.0) | (-38.0,  0.0) (-25.0,  3.0) (-38.0, 12.0)
 1   |       .              .             .       (-32.0,  0.0) |       .       (-48.0,  0.0) (-49.0,  9.0)
     |       .              .             .       (-41.0, -9.0) |       .             .       (-62.0,  0.0)

[ Top of Page | Previous Page | Next Page | Table of Contents | Index ]

Parallel Engineering and Scientific Subroutine Library for AIX Version 2 Release 3: Guide and Reference

PDSYR2K, PZSYR2K, and PZHER2K--Rank-2K Update of a Real or Complex Symmetric or a Complex Hermitian Matrix

Syntax

On Entry

On Return

Notes and Coding Rules

Error Conditions

Computational Errors

Resource Errors

Input-Argument and Miscellaneous Errors

Example 1

Call Statements and Input

Example 2

Call Statements and Input

Example 3

Call Statements and Input