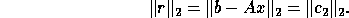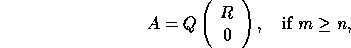




The most common, and best known, of the factorizations is the QR factorization given by
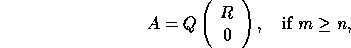
where R is an n-by-n upper triangular matrix and Q is an m-by-m orthogonal (or unitary) matrix. If A is of full rank n, then R is non-singular. It is sometimes convenient to write the factorization as
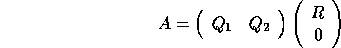
which reduces to

where 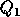 consists of the first n columns of Q, and
consists of the first n columns of Q, and 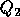 the
remaining m - n columns.
the
remaining m - n columns.
If m < n, R is trapezoidal, and the factorization can be written
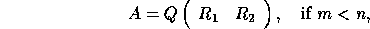
where 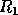 is upper triangular and
is upper triangular and 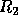 is rectangular.
is rectangular.
The routine xGEQRF
computes the QR factorization. The matrix Q is not
formed explicitly, but is represented as a product of elementary reflectors,
as described in section 5.4.
Users need not be aware of the details of this representation,
because associated routines are provided to work with Q:
xORGQR (or xUNGQR
in the complex case) can generate all or part of R,
while xORMQR (or xUNMQR ) can pre- or post-multiply
a given matrix by Q or 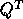 (
(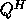 if complex).
if complex).
The QR factorization can be used to solve the linear least squares problem (2.1) when m > = n and A is of full rank, since
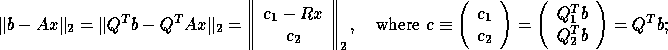
c can be computed by xORMQR (or xUNMQR
), and 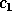 consists of its first
n elements. Then
x is the solution of the upper triangular system
consists of its first
n elements. Then
x is the solution of the upper triangular system

which can be computed by xTRTRS . The residual vector r is given by
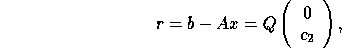
and may be computed using xORMQR (or xUNMQR
).
The residual sum of squares 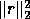 may be computed without forming r
explicitly, since
may be computed without forming r
explicitly, since