Engineering and Scientific Subroutine Library for AIX Version 3 Release 3: Guide and Reference

SDOTI, DDOTI, CDOTUI, ZDOTUI, CDOTCI, and ZDOTCI--Dot Product of a Sparse Vector X in Compressed-Vector Storage Mode and a Sparse Vector Y in Full-Vector Storage Mode

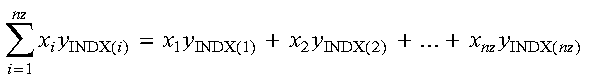
SDOTI, DDOTI, CDOTUI, and ZDOTUI compute the dot product of sparse vector x, stored in compressed-vector storage mode, and full vector y, stored in full-vector storage mode.

CDOTCI and ZDOTCI compute the dot product of the complex conjugate of sparse vector x, stored in compressed-vector storage mode, and full vector y, stored in full-vector storage mode.

Table 61. Data Types

Syntax

On Entry

nz

is the number of elements in sparse vector x, stored in compressed-vector storage mode. Specified as: a fullword integer; nz >= 0.

x

is the sparse vector x, containing nz elements, stored in compressed-vector storage mode in an array, referred to as X. Specified as: a one-dimensional array of (at least) length nz, containing numbers of the data type indicated in Table 61.

indx

is the array, referred to as INDX, containing the nz indices that indicate the positions of the elements of the sparse vector x when in full-vector storage mode. They also indicate the positions of elements in vector y that are used in the computation.

Specified as: a one-dimensional array of (at least) length nz, containing fullword integers.

y

is the sparse vector y, stored in full-vector storage mode, of (at least) length max(INDX(i)) for i = 1, nz. Specified as: a one-dimensional array of (at least) length max(INDX(i)) for i = 1, nz, containing numbers of the data type indicated in Table 61.

On Return

Function value

 

is the result of the dot product computation.

Returned as: a number of the data type indicated in Table 61.

Note

1. Declare this function in your program as returning a value of the data type indicated in Table 61.
2. For a description of how sparse vectors are stored, see Sparse Vector.

Function

For SDOTI, DDOTI, CDOTUI, and ZDOTUI, the dot product computation is expressed as follows:

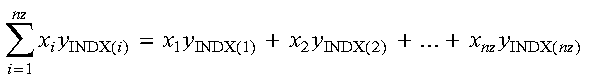
For CDOTCI and ZDOTCI, the dot product computation is expressed as follows:

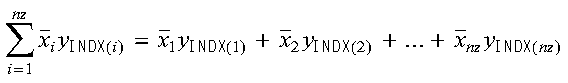
where:

x is a sparse vector, stored in compressed-vector storage mode.

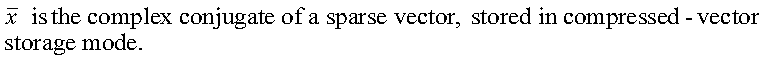
INDX is the indices array for sparse vector x.

y is a sparse vector, stored in full-vector storage mode.

See reference [29]. The result is returned as the function value. If nz is 0, then zero is returned as the value of the function.

For SDOTI, CDOTUI, and CDOTCI, intermediate results are accumulated in long-precision.

Error Conditions

Computational Errors

None

Input-Argument Errors

nz < 0

Example 1

This example shows how to use SDOTI to compute a dot product using a sparse vector x of length 5, where the elements of array INDX are in ascending order.

Function Reference and Input

              NZ  X   INDX   Y
              |   |    |     |
DOTT = SDOTI( 5 , X , INDX , Y )
 
X        =  (1.0, 2.0, 3.0, 4.0, 5.0)
INDX     =  (1, 3, 4, 7, 10)
Y        =  (1.0, 5.0, 4.0, 3.0, 6.0, 10.0, -2.0, 8.0, 9.0, 0.0)

Output

DOTT     =  (1.0 + 8.0 + 9.0 -8.0 + 0.0) = 10.0

Example 2

This example shows how to use SDOTI to compute a dot product using a sparse vector x of length 5, where the elements of array INDX are in random order.

Function Reference and Input

              NZ  X   INDX   Y
              |   |    |     |
DOTT = SDOTI( 5 , X , INDX , Y )
 
X        =  (1.0, 2.0, 3.0, 4.0, 5.0)
INDX     =  (4, 3, 1, 10, 7)
Y        =  (1.0, 5.0, 4.0, 3.0, 6.0, 10.0, -2.0, 8.0, 9.0, 0.0)

Output

DOTT     =  (3.0 + 8.0 + 3.0 + 0.0 -10.0) = 4.0

Example 3

This example shows how to use CDOTUI to compute a dot product using a sparse vector x of length 3, where the elements of array INDX are in ascending order.

Function Reference and Input

               NZ  X   INDX   Y
               |   |    |     |
DOTT = CDOTUI( 3 , X , INDX , Y )
 
X        =  ((1.0, 2.0), (3.0, 4.0), (5.0, 6.0))
INDX     =  (1, 3, 4)
Y        =  ((6.0, 5.0), (-2.0, 3.0), (15.0, 4.0), (9.0, 0.0))

Output

DOTT     =  (70.0, 143.0)

Example 4

This example shows how to use CDOTCI to compute a dot product using the complex conjugate of a sparse vector x of length 3, where the elements of array INDX are in random order.

Function Reference and Input

               NZ  X   INDX   Y
               |   |    |     |
DOTT = CDOTCI( 3 , X , INDX , Y )
 
X        =  ((1.0, 2.0), (3.0, 4.0), (5.0, 6.0))
INDX     =  (4, 1, 3)
Y        =  ((6.0, 5.0), (-2.0, 3.0), (15.0, 4.0), (9.0, 0.0))

Output

DOTT     =  (146.0, -97.0)