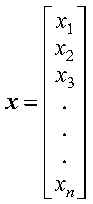

A vector is a one-dimensional, ordered collection of numbers. It can be a column vector, which represents an n by 1 ordered collection, or a row vector, which represents a 1 by n ordered collection.
The column vector appears symbolically as follows:
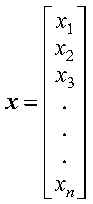
A row vector appears symbolically as follows:
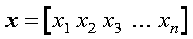
Vectors can contain either real or complex numbers. When they contain real numbers, they are sometimes called real vectors. When they contain complex numbers, they are called complex vectors.
The transpose of a vector changes a column vector to a row vector, or vice versa:
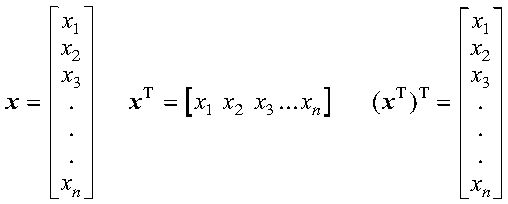
The ESSL subroutines use the vector as it is intended in the computation, as either a column vector or a row vector; therefore, no movement of data is necessary.
In the examples provided with the subroutine descriptions in Part 2, Reference Information of this book, both types of vectors are represented in the same way, showing the elements of the array that make up the vector x, as follows:
(1.0, 2.0, 3.0, 4.0, 5.0, 6.0)
The conjugate transpose of a vector x, containing complex numbers, is denoted by xH and is expressed as follows:
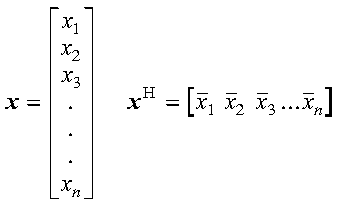
Just as for the transpose of a vector, no movement of data is necessary for the conjugate transpose of a vector.
A vector is usually stored within a one- or two-dimensional array. Its elements are stored sequentially in the array, but not necessarily contiguously.
The location of the vector in the array is specified by the argument for the vector in the ESSL calling sequence. It can be specified in a number of ways. For example, if A is an array of length 12, and you want to specify vector x as starting at the first element of array A, specify A as the argument, such as in:
X = SASUM (4,A,2)
where the number of elements to be summed in the vector is 4, the location of the vector is A, and the stride is 2.
If you want to specify vector x as starting at element 3 in array A, which is declared as A(1:12), specify:
X = SASUM (4,A(3),2)
If A is declared as A(-1:8), specify the following for element 3:
X = SASUM (4,A(1),2)
If A is a two-dimensional array and declared as A(1:4,1:10), and you want vector x to start at the second row and third column of A, specify the following:
X = SASUM (4,A(2,3),2)
The stride specified in the ESSL calling sequence is used to step through the array to select the vector elements. The direction in which the vector elements are selected from the array--that is, front to back or back to front--is indicated by the sign (+ or -) of the stride. The absolute value of the stride gives the spacing between each element selected from the array.
To calculate the total number of elements needed in an array for a vector, you can use the following formula, which takes into account the number of elements, n, in the array and the stride, inc, specified for the vector:
An array can be much larger than the vector that it contains; that is, there can be many elements following the vector in the array, as well as elements preceding the vector.
For a complete description of how vectors are stored within arrays, see How Stride Is Used for Vectors.
For a complex vector, a special storage arrangement is used to accommodate the two parts, a and b, of each complex number (a+bi) in the array. For each complex number, two sequential storage locations are required in the array. Therefore, exactly twice as much storage is required for complex vectors and matrices as for real vectors and matrices of the same precision. See How Do You Set Up Your Scalar Data? for a description of real and complex numbers, and How Do You Set Up Your Arrays? for a description of how real and complex data is stored in arrays.
The stride for a vector is an increment that is used to step through array storage to select the vector elements from an array. To define exactly which elements become the conceptual vector in the array, the following items are used together:
The stride can be positive, negative, or 0. For positive and negative strides, if you specify vector elements beyond the range of the array, your results are be unpredictable, and you may get program errors.
This section explains how each of the three types of stride is used to select the vector elements from the array.
When a positive stride is specified for a vector, the location specified by the argument for the vector is the location of the first element in the vector, element x1. The vector is in forward order in the array: (x1, x2, ..., xn). For example, if you specify X(1) for vector x, where X is declared as X(0:12) and defined as:
X = (1.0, 2.0, 3.0, 4.0, 5.0, 6.0, 7.0, 8.0, 9.0, 10.0, 11.0, 12.0, 13.0)
then processing begins at the second element in X, which is 2.0.
To find each successive element, the stride is added cumulatively to the starting point of vector x in the array. In this case, the starting point is X(1). If the stride specified for vector x is 3 and the number of elements to be processed is 4, then the resulting elements selected from X for vector x are: X(1),X(4),X(7), and X(10).
Vector x is then:
(2.0, 5.0, 8.0, 11.0)
As shown in this example, a vector does not have to extend to the end of the array. Elements are selected from the second to the eleventh element of the array, and the array elements after that are not used.
This element selection can be expressed in general terms. Using BEGIN as the starting point in an array X and inc as the stride, this results in the following elements being selected from the array:
The following general formula can be used to calculate each vector element position in a one-dimensional array:
When using an array with more than one dimension, you should understand how the array elements are stored to ensure that elements are selected properly. For a description of array storage, see Setting Up Arrays in Fortran. You should remember that the elements of an array are selected as they are arranged in storage, regardless of the number of dimensions defined in the array. Stride is used to step through array storage until n elements are selected. ESSL processing stops at that point. For example, given the following two-dimensional array, declared as A(1:7,1:4).
Matrix A is:
* *
| 1.0 8.0 15.0 22.0 |
| 2.0 9.0 16.0 23.0 |
| 3.0 10.0 17.0 24.0 |
| 4.0 11.0 18.0 25.0 |
| 5.0 12.0 19.0 26.0 |
| 6.0 13.0 20.0 27.0 |
| 7.0 14.0 21.0 28.0 |
* *
with A(3,1) specified for vector x, a stride of 2, and the number of elements to be processed as 12, the resulting vector x is:
(3.0, 5.0, 7.0, 9.0, 11.0, 13.0, 15.0, 17.0, 19.0, 21.0, 23.0, 25.0)
This is not a conventional use of arrays, and you should be very careful when using this technique.
When a zero stride is specified for a vector, the starting point for the vector is the only element used in the computation. The starting point for the vector is at the location specified by the argument for the vector, just as though you had specified a positive stride. For example, if you specify X for vector x, where X is defined as:
X = (5.0, 4.0, 3.0, 2.0, 1.0)
and you specify the number of elements, n, to be processed as 6, then processing begins at the first element, which is 5.0. This element is used for each of the six elements in vector x.
This makes the conceptual vector x appear as:
(5.0, 5.0, 5.0, 5.0, 5.0, 5.0)
The following general formula shows how to calculate each vector position in a one-dimensional array:
When a negative stride is specified for a vector, the location specified for the vector is actually the location of the last element in the vector. In other words, the vector is in reverse order in the array: (xn, xn-1, ..., x1). You specify the end of the vector, (xn). ESSL then calculates where the starting point (x1) is by using the following arguments:
If you specify vector x at location X(BEGIN) in array X with a negative stride of inc and n elements to be processed, then the following formula gives the starting point of vector x in the array:
For example, if you specify X(2) for vector x, where X is declared as X(1:9) and defined as:
X = (1.0, 2.0, 3.0, 4.0, 5.0, 6.0, 7.0, 8.0, 9.0)
and if you specify a stride of -2, and four elements to be processed, processing begins at the following element in X:
where element X(8) is 8.0.
To find each of the n successive element positions in the array, you successively add the stride to the starting point n-1 times. Suppose the formula calculated a starting point of X(SP); the elements selected are:
In the above example, the resulting elements selected from X for vector x are X(8), X(6), X(4), and X(2). This makes the resulting vector x appear as follows:
(8.0, 6.0, 4.0, 2.0)
The following general formula can be used to calculate each vector element position in a one-dimensional array:
A sparse vector is a vector having a relatively small number of nonzero elements.
Consider the following as an example of a sparse vector x with n elements, where n is 11, and vector x is:
(0.0, 0.0, 1.0, 0.0, 2.0, 3.0, 0.0, 4.0, 0.0, 5.0, 0.0)
There are two storage modes that apply to sparse vectors: full-vector storage mode and compressed-vector storage mode. When a sparse vector is stored in full-vector storage mode, all its elements, including its zero elements, are stored in an array.
For example, sparse vector x is stored in full-vector storage mode in a one-dimensional array X, as follows:
X = (0.0, 0.0, 1.0, 0.0, 2.0, 3.0, 0.0, 4.0, 0.0, 5.0, 0.0)
When a sparse vector is stored in compressed-vector storage mode, it is stored without its zero elements. It consists of two one-dimensional arrays, each with a length of nz, where nz is the number of nonzero elements in vector x:
For example, the sparse vector x shown above might have its five nonzero elements stored in ascending order in array X of length 5, as follows:
X = (1.0, 2.0, 3.0, 4.0, 5.0)
in which case, the array of indices, INDX, also of length 5, contains:
INDX = (3, 5, 6, 8, 10)
If the sparse vector x has its elements stored in random order in the array X as:
X = (5.0, 3.0, 4.0, 1.0, 2.0)
then the array INDX contains:
INDX = (10, 6, 8, 3, 5)
In general terms, this storage technique can be expressed as follows:
where:
To avoid an error when using the INDX array to access the elements in any other target vector, the length of the target vector must be greater than or equal to max(INDX(i)) for i = 1, nz.