Engineering and Scientific Subroutine Library for AIX Version 3 Release 3: Guide and Reference

SGER, DGER, CGERU, ZGERU, CGERC, and ZGERC--Rank-One Update of a General Matrix

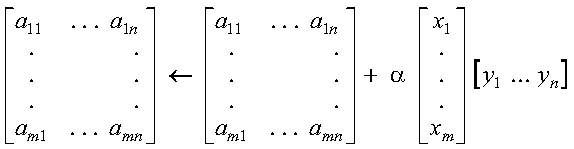
SGER, DGER, CGERU, and ZGERU compute the rank-one update of a general matrix, using the scalar alpha, matrix A, vector x, and the transpose of vector y:

A <-- A+alphaxy^T

CGERC and ZGERC compute the rank-one update of a general matrix, using the scalar alpha, matrix A, vector x, and the conjugate transpose of vector y:

A <-- A+alphaxy^H

Table 63. Data Types

Note:

For compatibility with earlier releases of ESSL, you can use the names SGER1 and DGER1 for SGER and DGER, respectively.

Syntax

On Entry

m

is the number of rows in matrix A and the number of elements in vector x. Specified as: a fullword integer; 0 <= m <= lda.

n

is the number of columns in matrix A and the number of elements in vector y. Specified as: a fullword integer; n >= 0.

alpha

is the scaling constant alpha. Specified as: a number of the data type indicated in Table 63.

x

is the vector x of length m. Specified as: a one-dimensional array of (at least) length 1+(m-1)|incx|, containing numbers of the data type indicated in Table 63.

incx

is the stride for vector x. Specified as: a fullword integer. It can have any value.

y

is the vector y of length n, whose transpose or conjugate transpose is used in the computation.

Note:

No data should be moved to form y^T or y^H; that is, the vector y should always be stored in its untransposed form.

Specified as: a one-dimensional array of (at least) length 1+(n-1)|incy|, containing numbers of the data type indicated in Table 63.

incy

is the stride for vector y. Specified as: a fullword integer. It can have any value.

a

is the m by n matrix A. Specified as: an lda by (at least) n array, containing numbers of the data type indicated in Table 63.

lda

is the size of the leading dimension of the array specified for a. Specified as: a fullword integer; lda > 0 and lda >= m.

On Return

a

is the m by n matrix A, containing the result of the computation.

Returned as: a two-dimensional array, containing numbers of the data type indicated in Table 63.

Notes

1. In these subroutines, incx = 0 and incy = 0 are valid; however, the Level 2 BLAS standard considers incx = 0 and incy = 0 to be invalid. See references [34] and [35].
2. Matrix A can have no common elements with vectors x and y; otherwise, results are unpredictable. See Concepts.

Function

SGER, DGER, CGERU, and ZGERU compute the rank-one update of a general matrix:

A <-- A+alphaxy^T

where:

A is an m by n matrix.

alpha is a scalar.

x is a vector of length m.

y^T is the transpose of vector y of length n.

It is expressed as follows:

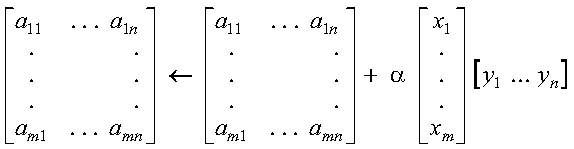
It can also be expressed as:

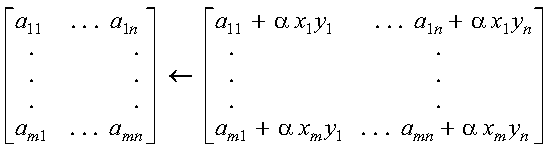
CGERC and ZGERC compute a slightly different rank-one update of a general matrix:

A <-- A+alphaxy^H

where:

A is an m by n matrix.

alpha is a scalar.

x is a vector of length m.

y^H is the conjugate transpose of vector y of length n.

It is expressed as follows:

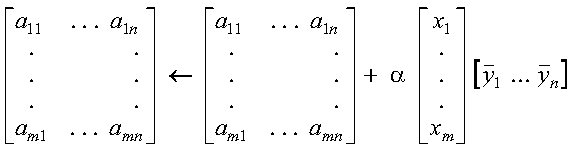
It can also be expressed as:

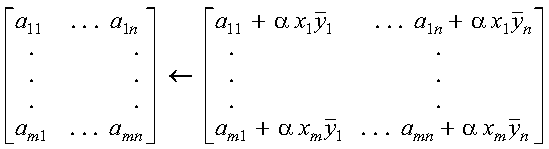
See references [34], [35], and [79]. No computation is performed if m, n, or alpha is zero. For CGERU and CGERC, intermediate results are accumulated in long precision. For SGER, intermediate results are accumulated in long precision on some platforms.

Error Conditions

Resource Errors

Unable to allocate internal work area.

Computational Errors

None

Input-Argument Errors

1. m < 0
2. n < 0
3. lda <= 0
4. m > lda

Example 1

This example shows a matrix, A, contained in a larger array, A. The strides of vectors x and y are positive. Because lda is 10 and n is 3, array A must be declared as A(E1:E2,F1:F2), where E2-E1+1=10 and F2-F1+1 >= 3. For this example, array A is declared as A(1:10,0:2).

Call Statement and Input

           M   N  ALPHA  X  INCX  Y  INCY    A     LDA
           |   |    |    |   |    |   |      |      |
CALL SGER( 4 , 3 , 1.0 , X , 1  , Y , 2  , A(1,0) , 10 )
 
X        =  (3.0, 2.0, 1.0, 4.0)
Y        =  (1.0, . , 2.0, . , 3.0)

    *               *
    | 1.0  2.0  3.0 |
    | 2.0  2.0  4.0 |
    | 3.0  2.0  2.0 |
    | 4.0  2.0  1.0 |
A = |  .    .    .  |
    |  .    .    .  |
    |  .    .    .  |
    |  .    .    .  |
    |  .    .    .  |
    |  .    .    .  |
    *               *

Output

    *                 *
    | 4.0   8.0  12.0 |
    | 4.0   6.0  10.0 |
    | 4.0   4.0   5.0 |
    | 8.0  10.0  13.0 |
A = |  .     .     .  |
    |  .     .     .  |
    |  .     .     .  |
    |  .     .     .  |
    |  .     .     .  |
    |  .     .     .  |
    *                 *

Example 2

This example shows a matrix, A, contained in a larger array, A. The strides of vectors x and y are of opposite sign. For y, which has negative stride, processing begins at element Y(5), which is 1.0. Array A must follow the same rules as given in Example 1. For this example, array A is declared as A(-1:8,1:3).

Call Statement and Input

           M   N  ALPHA  X  INCX  Y   INCY     A     LDA
           |   |    |    |   |    |    |       |      |
CALL SGER( 4 , 3 , 1.0 , X , 1  , Y , -2  , A(-1,1) , 10 )

Output

Example 3

This example shows a matrix, A, contained in a larger array, A, and the first element of the matrix is not the first element of the array. Array A must follow the same rules as given in Example 1. For this example, array A is declared as A(1:10,1:3).

Call Statement and Input

           M   N  ALPHA  X  INCX  Y  INCY    A     LDA
           |   |    |    |   |    |   |      |      |
CALL SGER( 4 , 3 , 1.0 , X , 3  , Y , 1  , A(4,1) , 10 )
 
X        =  (3.0, . , . , 2.0, . , . , 1.0, . , . , 4.0)
Y        =  (1.0, 2.0, 3.0)

    *               *
    | .    .    .   |
    | .    .    .   |
    | .    .    .   |
    | 1.0  2.0  3.0 |
A = | 2.0  2.0  4.0 |
    | 3.0  2.0  2.0 |
    | 4.0  2.0  1.0 |
    |  .    .    .  |
    |  .    .    .  |
    |  .    .    .  |
    *               *

Output

    *                 *
    | .     .     .   |
    | .     .     .   |
    | .     .     .   |
    | 4.0   8.0  12.0 |
A = | 4.0   6.0  10.0 |
    | 4.0   4.0   5.0 |
    | 8.0  10.0  13.0 |
    |  .     .     .  |
    |  .     .     .  |
    |  .     .     .  |
    *                 *

Example 4

This example shows a matrix, A, and array, A, having the same number of rows. For this case, m and lda are equal. Because lda is 4 and n is 3, array A must be declared as A(E1:E2,F1:F2), where E2-E1+1=4 and F2-F1+1 >= 3. For this example, array A is declared as A(1:4,0:2).

Call Statement and Input

           M   N  ALPHA  X  INCX  Y  INCY    A     LDA
           |   |    |    |   |    |   |      |      |
CALL SGER( 4 , 3 , 1.0 , X , 1  , Y , 1  , A(1,0) , 4 )
 
X        =  (3.0, 2.0, 1.0, 4.0)
Y        =  (1.0, 2.0, 3.0)

    *               *
    | 1.0  2.0  3.0 |
A = | 2.0  2.0  4.0 |
    | 3.0  2.0  2.0 |
    | 4.0  2.0  1.0 |
    *               *

Output

    *                 *
    | 4.0   8.0  12.0 |
A = | 4.0   6.0  10.0 |
    | 4.0   4.0   5.0 |
    | 8.0  10.0  13.0 |
    *                 *

Example 5

This example shows a computation in which scalar value for alpha is greater than 1. Array A must follow the same rules as given in Example 4. For this example, array A is declared as A(-1:2,1:3).

Call Statement and Input

           M   N  ALPHA  X  INCX  Y  INCY     A     LDA
           |   |    |    |   |    |   |       |      |
CALL SGER( 4 , 3 , 2.0 , X , 1  , Y , 1  , A(-1,1) , 4 )

Output

    *                  *
    |  7.0  14.0  21.0 |
A = |  6.0  10.0  16.0 |
    |  5.0   6.0   8.0 |
    | 12.0  18.0  25.0 |
    *                  *

Example 6

This example shows a rank-one update in which all data items contain complex numbers, and the transpose y^T is used in the computation. Matrix A is contained in a larger array, A. The strides of vectors x and y are positive. The Fortran DIMENSION statement for array A must follow the same rules as given in Example 1. For this example, array A is declared as A(1:10,0:2).

Call Statement and Input

            M   N   ALPHA   X  INCX  Y  INCY    A     LDA
            |   |     |     |   |    |   |      |      |
CALL CGERU( 5 , 3 , ALPHA , X , 1  , Y , 1  , A(1,0) , 10 )
 
ALPHA    =  (1.0, 0.0)
X        =  ((1.0, 2.0), (4.0, 0.0), (1.0, 1.0), (3.0, 4.0),
             (2.0, 0.0))
Y        =  ((1.0, 2.0), (4.0, 0.0), (1.0, -1.0))

    *                                    *
    | (1.0, 2.0)  (3.0, 5.0)  (2.0, 0.0) |
    | (2.0, 3.0)  (7.0, 9.0)  (4.0, 8.0) |
    | (7.0, 4.0)  (1.0, 4.0)  (6.0, 0.0) |
    | (8.0, 2.0)  (2.0, 5.0)  (8.0, 0.0) |
A = | (9.0, 1.0)  (3.0, 6.0)  (1.0, 0.0) |
    |     .           .           .      |
    |     .           .           .      |
    |     .           .           .      |
    |     .           .           .      |
    |     .           .           .      |
    *                                    *

Output

    *                                             *
    | (-2.0,   6.0)   (7.0,  13.0)   (5.0,   1.0) |
    |  (6.0,  11.0)  (23.0,   9.0)   (8.0,   4.0) |
    |  (6.0,   7.0)   (5.0,   8.0)   (8.0,   0.0) |
    |  (3.0,  12.0)  (14.0,  21.0)  (15.0,   1.0) |
A = | (11.0,   5.0)  (11.0,   6.0)   (3.0,  -2.0) |
    |      .              .              .        |
    |      .              .              .        |
    |      .              .              .        |
    |      .              .              .        |
    |      .              .              .        |
    *                                             *

Example 7

This example shows a rank-one update in which all data items contain complex numbers, and the conjugate transpose y^H is used in the computation. Matrix A is contained in a larger array, A. The strides of vectors x and y are positive. The Fortran DIMENSION statement for array A must follow the same rules as given in Example 1. For this example, array A is declared as A(1:10,0:2).

Call Statement and Input

            M   N   ALPHA   X  INCX  Y  INCY    A     LDA
            |   |     |     |   |    |   |      |      |
CALL CGERC( 5 , 3 , ALPHA , X , 1  , Y , 1  , A(1,0) , 10 )

Output

    *                                            *
    |  (6.0,   2.0)   (7.0,  13.0)  (1.0,   3.0) |
    |  (6.0,  -5.0)  (23.0,   9.0)  (8.0,  12.0) |
    | (10.0,   3.0)   (5.0,   8.0)  (6.0,   2.0) |
    | (19.0,   0.0)  (14.0,  21.0)  (7.0,   7.0) |
A = | (11.0,  -3.0)  (11.0,   6.0)  (3.0,   2.0) |
    |      .              .             .        |
    |      .              .             .        |
    |      .              .             .        |
    |      .              .             .        |
    |      .              .             .        |
    *                                            *