Engineering and Scientific Subroutine Library for AIX Version 3 Release 3: Guide and Reference

SSPMV, DSPMV, CHPMV, ZHPMV, SSYMV, DSYMV, CHEMV, ZHEMV, SSLMX, and DSLMX--Matrix-Vector Product for a Real Symmetric or Complex Hermitian Matrix

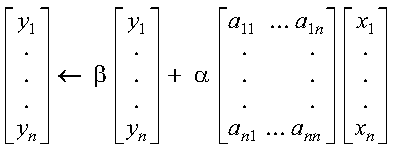
SSPMV, DSPMV, CHPMV, ZHPMV, SSYMV, DSYMV, CHEMV, and ZHEMV compute the matrix-vector product for either a real symmetric matrix or a complex Hermitian matrix, using the scalars alpha and beta, matrix A, and vectors x and y:

y<--betay+alphaAx

SSLMX and DSLMX compute the matrix-vector product for a real symmetric matrix, using the scalar alpha, matrix A, and vectors x and y:

y<--y+alphaAx

The following storage modes are used:

• For SSPMV, DSPMV, CHPMV, and ZHPMV, matrix A is stored in upper- or lower-packed storage mode.
• For SSYMV, DSYMV, CHEMV, and ZHEMV, matrix A is stored in upper or lower storage mode.
• For SSLMX and DSLMX, matrix A is stored in lower-packed storage mode.

Table 64. Data Types

Note:

SSPMV and DSPMV are Level 2 BLAS subroutines. You should use these subroutines instead of SSLMX and DSLMX, which are provided only for compatibility with earlier releases of ESSL.

Syntax

On Entry

uplo

indicates the storage mode used for matrix A, where:

If uplo = 'U', A is stored in upper-packed or upper storage mode.

If uplo = 'L', A is stored in lower-packed or lower storage mode.

Specified as: a single character. It must be 'U' or 'L'.

n

is the number of elements in vectors x and y and the order of matrix A. Specified as: a fullword integer; n >= 0.

alpha

is the scaling constant alpha. Specified as: a number of the data type indicated in Table 64.

ap

has the following meaning:

For SSPMV and DSPMV, ap is the real symmetric matrix A of order n, stored in upper- or lower-packed storage mode.

For CHPMV and ZHPMV, ap is the complex Hermitian matrix A of order n, stored in upper- or lower-packed storage mode.

For SSLMX and DSLMX, ap is the real symmetric matrix A of order n, stored in lower-packed storage mode.

Specified as: a one-dimensional array of (at least) length n(n+1)/2, containing numbers of the data type indicated in Table 64.

a

has the following meaning:

For SSYMV and DSYMV, a is the real symmetric matrix A of order n, stored in upper or lower storage mode.

For CHEMV and ZHEMV, a is the complex Hermitian matrix A of order n, stored in upper or lower storage mode.

Specified as: an lda by (at least) n array, containing numbers of the data type indicated in Table 64.

lda

is the leading dimension of the array specified for a. Specified as: a fullword integer; lda > 0 and lda >= n.

x

is the vector x of length n. Specified as: a one-dimensional array of (at least) length 1+(n-1)|incx|, containing numbers of the data type indicated in Table 64.

incx

is the stride for vector x. Specified as: a fullword integer, where:

For SSPMV, DSPMV, CHPMV, ZHPMV, SSYMV, DSYMV, CHEMV, and ZHEMV, incx < 0 or incx > 0.

For SSLMX and DSLMX, incx can have any value.

beta

is the scaling constant beta. Specified as: a number of the data type indicated in Table 64.

y

is the vector y of length n. Specified as: a one-dimensional array of (at least) length 1+(n-1)|incy|, containing numbers of the data type indicated in Table 64.

incy

is the stride for vector y. Specified as: a fullword integer; incy > 0 or incy < 0.

On Return

y

is the vector y of length n, containing the result of the computation. Returned as: a one-dimensional array, containing numbers of the data type indicated in Table 64.

Notes

1. All subroutines accept lowercase letters for the uplo argument.
2. The vector y must have no common elements with vector x or matrix A; otherwise, results are unpredictable. See Concepts.
3. On input, the imaginary parts of the diagonal elements of the complex Hermitian matrix A are assumed to be zero, so you do not have to set these values.
4. For a description of how symmetric matrices are stored in upper- or lower-packed storage mode and upper or lower storage mode, see Symmetric Matrix. For a description of how complex Hermitian matrices are stored in upper- or lower-packed storage mode and upper or lower storage mode, see Complex Hermitian Matrix.

Function

These subroutines perform the computations described in the two sections below. See references [34], [35], and [79]. For SSPMV, DSPMV, CHPMV, ZHPMV, SSYMV, DSYMV, CHEMV, and ZHEMV, if n is zero or if alpha is zero and beta is one, no computation is performed. For SSLMX and DSLMX, if n or alpha is zero, no computation is performed.

For SSLMX, SSPMV, SSYMV, CHPMV, and CHEMV, intermediate results are accumulated in long precision. However, several intermediate stores may occur for each element of the vector y.

For SSPMV, DSPMV, CHPMV, ZHPMV, SSYMV, DSYMV, CHEMV, and ZHEMV

These subroutines compute the matrix-vector product for either a real symmetric matrix or a complex Hermitian matrix:

y<--betay+alphaAx

where:

y is a vector of length n.

alpha is a scalar.

beta is a scalar.

A is a real symmetric or complex Hermitian matrix of order n.

x is a vector of length n.

It is expressed as follows:

For SSLMX and DSLMX

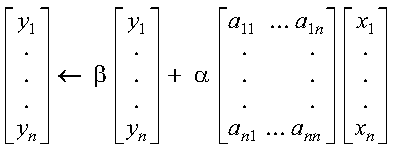
These subroutines compute the matrix-vector product for a real symmetric matrix stored in lower-packed storage mode:

y<--y+alphaAx

where:

y is a vector of length n.

alpha is a scalar.

A is a real symmetric matrix of order n.

x is a vector of length n.

It is expressed as follows:

Error Conditions

Computational Errors

None

Input-Argument Errors

1. uplo <>  'L' or 'U'
2. n < 0
3. lda < n
4. lda <= 0
5. incx = 0
6. incy = 0

Example 1

This example shows vectors x and y with positive strides and a real symmetric matrix A of order 3, stored in lower-packed storage mode. Matrix A is:

                      *               *
                      | 8.0  4.0  2.0 |
                      | 4.0  6.0  7.0 |
                      | 2.0  7.0  3.0 |
                      *               *

Call Statement and Input

            UPLO  N  ALPHA  AP   X  INCX BETA  Y  INCY
             |    |    |     |   |   |    |    |   |
CALL SSPMV( 'L' , 3 , 1.0 , AP , X , 1 , 1.0 , Y , 2 )
 
AP       =  (8.0, 4.0, 2.0, 6.0, 7.0, 3.0)
X        =  (3.0, 2.0, 1.0)
Y        =  (5.0, . , 3.0, . , 2.0)

Output

Y        =  (39.0, . , 34.0, . , 25.0)

Example 2

This example shows vector x and y having strides of opposite signs. For x, which has negative stride, processing begins at element X(5), which is 1.0. The real symmetric matrix A of order 3 is stored in upper-packed storage mode. It uses the same input matrix A as in Example 1.

Call Statement and Input

            UPLO  N  ALPHA  AP   X  INCX  BETA  Y  INCY
             |    |    |     |   |    |    |    |   |
CALL SSPMV( 'U' , 3 , 1.0 , AP , X , -2 , 2.0 , Y , 1 )
 
AP       =  (8.0, 4.0, 6.0, 2.0, 7.0, 3.0)
X        =  (4.0, . , 2.0, . , 1.0)
Y        =  (6.0, 5.0, 4.0)

Output

Y        =  (36.0, 54.0, 36.0)

Example 3

This example shows vector x and y with positive stride and a complex Hermitian matrix A of order 3, stored in lower-packed storage mode. Matrix A is:

            *                                      *
            |  (1.0, 0.0)  (3.0, 5.0)  (2.0, -3.0) |
            | (3.0, -5.0)  (7.0, 0.0)  (4.0, -8.0) |
            |  (2.0, 3.0)  (4.0, 8.0)   (6.0, 0.0) |
            *                                      *

Note:

On input, the imaginary parts of the diagonal elements of the complex Hermitian matrix A are assumed to be zero, so you do not have to set these values.

Call Statement and Input

            UPLO  N   ALPHA   AP   X  INCX BETA   Y  INCY
             |    |     |      |   |   |    |     |   |
CALL CHPMV( 'L' , 3 , ALPHA , AP , X , 1 , BETA , Y , 2 )

ALPHA    =  (1.0, 0.0)
AP       =  ((1.0, . ), (3.0, -5.0), (2.0, 3.0), (7.0, . ),
             (4.0, 8.0), (6.0, . ))
X        =  ((1.0, 2.0), (4.0, 0.0), (3.0, 4.0))
BETA     =  (1.0, 0.0)
Y        =  ((1.0, 0.0), . , (2.0, -1.0), . , (2.0, 1.0))

Output

Y        =  ((32.0, 21.0), . , (87.0, -8.0), . , (32.0, 64.0))

Example 4

This example shows vector x and y having strides of opposite signs. For x, which has negative stride, processing begins at element X(5), which is (1.0, 2.0). The complex Hermitian matrix A of order 3 is stored in upper-packed storage mode. It uses the same input matrix A as in Example 3.

Note:

On input, the imaginary parts of the diagonal elements of the complex Hermitian matrix A are assumed to be zero, so you do not have to set these values.

Call Statement and Input

            UPLO  N   ALPHA   AP   X  INCX  BETA   Y INCY
             |    |     |     |    |    |    |     |   |
CALL CHPMV( 'U' , 3 , ALPHA , AP , X , -2 , BETA , Y , 2 )

Output

Y        =  ((31.0, 21.0), . , (85.0, -7.0), . , (30.0, 63.0))

Example 5

This example shows vectors x and y with positive strides and a real symmetric matrix A of order 3, stored in lower storage mode. It uses the same input matrix A as in Example 1.

Call Statement and Input

            UPLO  N  ALPHA  A  LDA  X  INCX BETA  Y INCY
             |    |    |    |   |   |   |    |    |   |
CALL SSYMV( 'L' , 3 , 1.0 , A , 3 , X , 1 , 1.0 , Y , 2 )
 
    *               *
    | 8.0  .    .   |
A = | 4.0  6.0  .   |
    | 2.0  7.0  3.0 |
    *               *
 
X        =  (3.0, 2.0, 1.0)
Y        =  (5.0, . , 3.0, . , 2.0)

Output

Y        =  (39.0, . , 34.0, . , 25.0)

Example 6

This example shows vector x and y having strides of opposite signs. For x, which has negative stride, processing begins at element X(5), which is 1.0. The real symmetric matrix A of order 3 is stored in upper storage mode. It uses the same input matrix A as in Example 1.

Call Statement and Input

            UPLO  N  ALPHA  A  LDA  X  INCX  BETA  Y  INCY
             |    |    |    |   |   |    |    |    |   |
CALL SSYMV( 'U' , 3 , 1.0 , A , 4 , X , -2 , 2.0 , Y , 1 )
 
    *               *
    | 8.0  4.0  2.0 |
A = |  .   6.0  7.0 |
    |  .    .   3.0 |
    |  .    .    .  |
    *               *
 
X        =  (4.0, . , 2.0, . , 1.0)
Y        =  (6.0, 5.0, 4.0)

Output

A        =  (36.0, 54.0, 36.0)

Example 7

This example shows vector x and y with positive stride and a complex Hermitian matrix A of order 3, stored in lower storage mode. It uses the same input matrix A as in Example 3.

Note:

On input, the imaginary parts of the diagonal elements of the complex Hermitian matrix A are assumed to be zero, so you do not have to set these values.

Call Statement and Input

            UPLO  N   ALPHA   A  LDA  X  INCX BETA   Y INCY
             |    |     |     |   |   |   |    |     |   |
CALL CHEMV( 'L' , 3 , ALPHA , A , 3 , X , 1 , BETA , Y , 2 )
 
ALPHA    =  (1.0, 0.0)
 
        *                                    *
        | (1.0,  . )       .          .      |
A    =  | (3.0, -5.0)  (7.0, .  )     .      |
        | (2.0,  3.0)  (4.0, 8.0) (6.0,  . ) |
        *                                    *
 
X        =  ((1.0, 2.0), (4.0, 0.0), (3.0, 4.0))
BETA     =  (1.0, 0.0)
Y        =  ((1.0, 0.0), . , (2.0, -1.0), . , (2.0, 1.0))

Output

Y        =  ((32.0, 21.0), . , (87.0, -8.0), . , (32.0, 64.0))

Example 8

This example shows vector x and y having strides of opposite signs. For x, which has negative stride, processing begins at element X(5), which is (1.0, 2.0). The complex Hermitian matrix A of order 3 is stored in upper storage mode. It uses the same input matrix A as in Example 3.

Note:

On input, the imaginary parts of the diagonal elements of the complex Hermitian matrix A are assumed to be zero, so you do not have to set these values.

Call Statement and Input

            UPLO  N   ALPHA   A  LDA  X  INCX  BETA   Y INCY
             |    |     |     |   |   |    |    |     |   |
CALL CHEMV( 'U' , 3 , ALPHA , A , 3 , X , -2 , BETA , Y , 2 )
 
ALPHA    =  (1.0, 0.0)

        *                                    *
        | (1.0, . )  (3.0, 5.0)  (2.0, -3.0) |
A    =  |     .      (7.0,  . )  (4.0, -8.0) |
        |     .          .       (6.0,   . ) |
        *                                    *

Output

Y        =  ((31.0, 21.0), . , (85.0, -7.0), . , (30.0, 63.0))

Example 9

This example shows vectors x and y with positive strides and a real symmetric matrix A of order 3. Matrix A is:

                    *               *
                    | 8.0  4.0  2.0 |
                    | 4.0  6.0  7.0 |
                    | 2.0  7.0  3.0 |
                    *               *

Call Statement and Input

            N  ALPHA  AP   X  INCX  Y  INCY
            |    |    |    |   |    |   |
CALL SSLMX( 3 , 1.0 , AP , X , 1  , Y , 2  )
 
AP       =  (8.0, 4.0, 2.0, 6.0, 7.0, 3.0)
X        =  (3.0, 2.0, 1.0)
Y        =  (5.0, . , 3.0, . , 2.0)

Output

Y        =  (39.0, . , 34.0, . , 25.0)