Engineering and Scientific Subroutine Library for AIX Version 3 Release 3: Guide and Reference

DSMMX--Matrix-Vector Product for a Sparse Matrix in Compressed-Matrix Storage Mode

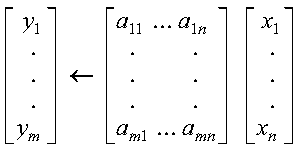
This subprogram computes the matrix-vector product for sparse matrix A, stored in compressed-matrix storage mode, using the matrix and vectors x and y:

y<--Ax

where A, x, and y contain long-precision real numbers. You can use DSMTM to transpose matrix A before calling this subroutine. The resulting computation performed by this subroutine is then y<--A^Tx.

Syntax

On Entry

m

is the number of rows in sparse matrix A and the number of elements in vector y. Specified as: a fullword integer; m >= 0.

nz

is the maximum number of nonzero elements in each row of sparse matrix A. Specified as: a fullword integer; nz >= 0.

ac

is the m by n sparse matrix A, stored in compressed-matrix storage mode in an array, referred to as AC. Specified as: an lda by (at least) nz array, containing long-precision real numbers.

ka

is the array, referred to as KA, containing the column numbers of the matrix A elements stored in the corresponding positions in array AC. Specified as: an lda by (at least) nz array, containing fullword integers, where 1 <= (elements of KA) <= n.

lda

is the size of the leading dimension of the arrays specified for ac and ka. Specified as: a fullword integer; lda > 0 and lda >= m.

x

is the vector x of length n. Specified as: a one-dimensional array of (at least) length n, containing long-precision real numbers.

y

See On Return.

On Return

y

is the vector y of length m, containing the result of the computation. Returned as: a one-dimensional array of (at least) length m, containing long-precision real numbers.

Notes

1. Matrix A must have no common elements with vectors x and y; otherwise, results are unpredictable.
2. For the KA array, where there are no corresponding nonzero elements in AC, you must still fill in a number between 1 and n. See the Example.
3. For a description of how sparse matrices are stored in compressed-matrix storage mode, see Compressed-Matrix Storage Mode.
4. If your sparse matrix is stored by rows, as defined in Storage-by-Rows, you should first use the DSRSM utility subroutine, described in DSRSM--Convert a Sparse Matrix from Storage-by-Rows to Compressed-Matrix Storage Mode, to convert your sparse matrix to compressed-matrix storage mode.

Function

The matrix-vector product is computed for a sparse matrix, stored in compressed matrix mode:

y<--Ax

where:

A is an m by n sparse matrix, stored in compressed-matrix storage mode in arrays AC and KA.

x is a vector of length n.

y is a vector of length m.

It is expressed as follows:

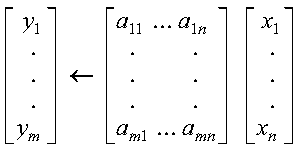
See reference [73]. If m is 0, no computation is performed; if nz is 0, output vector y is set to zero, because matrix A contains all zeros.

If your program uses a sparse matrix stored by rows and you want to use this subroutine, you should first convert your sparse matrix to compressed-matrix storage mode by using the DSRSM utility subroutine described in DSRSM--Convert a Sparse Matrix from Storage-by-Rows to Compressed-Matrix Storage Mode.

Error Conditions

Computational Errors

None

Input-Argument Errors

1. m < 0
2. lda <= 0
3. m > lda
4. nz < 0

Example

This example shows the matrix-vector product computed for the following sparse matrix A, which is stored in compressed-matrix storage mode in arrays AC and KA. Matrix A is:

                     *                              *
                     | 4.0  0.0  7.0  0.0  0.0  0.0 |
                     | 3.0  4.0  0.0  2.0  0.0  0.0 |
                     | 0.0  2.0  4.0  0.0  4.0  0.0 |
                     | 0.0  0.0  7.0  4.0  0.0  1.0 |
                     | 1.0  0.0  0.0  3.0  4.0  0.0 |
                     | 1.0  1.0  0.0  0.0  3.0  4.0 |
                     *                              *

Call Statement and Input

            M   NZ  AC   KA  LDA  X   Y
            |   |   |    |    |   |   |
CALL DSMMX( 6 , 4 , AC , KA , 6 , X , Y )

        *                    *
        | 4.0  7.0  0.0  0.0 |
        | 4.0  3.0  2.0  0.0 |
AC   =  | 4.0  2.0  4.0  0.0 |
        | 4.0  7.0  1.0  0.0 |
        | 4.0  1.0  3.0  0.0 |
        | 4.0  1.0  1.0  3.0 |
        *                    *

        *            *
        | 1  3  1  1 |
        | 2  1  4  1 |
KA   =  | 3  2  5  1 |
        | 4  3  6  1 |
        | 5  1  4  1 |
        | 6  1  2  5 |
        *            *
X        =  (1.0, 2.0, 3.0, 4.0, 5.0, 6.0)

Output

Y        =  (25.0, 19.0, 36.0, 43.0, 33.0, 42.0)