Engineering and Scientific Subroutine Library for AIX Version 3 Release 3: Guide and Reference

DSDMX--Matrix-Vector Product for a Sparse Matrix or Its Transpose in Compressed-Diagonal Storage Mode

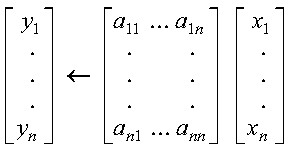
This subprogram computes the matrix-vector product for square sparse matrix A, stored in compressed-diagonal storage mode, using either the matrix or its transpose, and vectors x and y:

y<--Ax

y<--A^Tx

where A, x, and y contain long-precision real numbers.

Syntax

On Entry

iopt

indicates the storage variation used for sparse matrix A, stored in compressed-diagonal storage mode, where:

If iopt = 0, matrix A is a general sparse matrix, where all the nonzero diagonals in matrix A are used to set up the storage arrays.

If iopt = 1, matrix A is a symmetric sparse matrix, where only the nonzero main diagonal and one of each of the unique nonzero diagonals are used to set up the storage arrays.

Specified as: a fullword integer; iopt = 0 or 1.

n

is the order of sparse matrix A and the number of elements in vectors x and y. Specified as: a fullword integer; n >= 0.

nd

is the number of diagonals stored in the columns of array AD, as well as the number of columns in AD and the number of elements in array LA. Specified as: a fullword integer; nd >= 0.

ad

is the sparse matrix A of order n, stored in compressed diagonal storage in an array, referred to as AD. The iopt argument indicates the storage variation used for storing matrix A. The trans argument indicates the following:

If trans = 'N', A is used in the computation.

If trans = 'T', A^T is used in the computation.

Note:

No data should be moved to form A^T; that is, the matrix A should always be stored in its untransposed form.

Specified as: an lda by (at least) nd array, containing long-precision real numbers; lda >= n.

lda

is the size of the leading dimension of the array specified for ad. Specified as: a fullword integer; lda > 0 and lda >= n.

trans

indicates the form of matrix A to use in the computation, where:

If trans = 'N', A is used in the computation.

If trans = 'T', A^T is used in the computation.

Specified as: a single character; trans = 'N' or 'T'.

la

is the array, referred to as LA, containing the diagonal numbers k for the diagonals stored in each corresponding column in array AD. (For an explanation of how diagonal numbers are assigned, see Compressed-Diagonal Storage Mode.)

Specified as: a one-dimensional array of (at least) length nd, containing fullword integers; 1-n <= LA(i) <= n-1.

x

is the vector x of length n. Specified as: a one-dimensional array, containing long-precision real numbers.

y

See On Return.

On Return

y

is the vector y of length n, containing the result of the computation. Returned as: a one-dimensional array, containing long-precision real numbers.

Notes

1. All subroutines accept lowercase letters for the trans argument.
2. Matrix A must have no common elements with vectors x and y; otherwise, results are unpredictable.
3. For a description of how sparse matrices are stored in compressed-diagonal storage mode, see Compressed-Diagonal Storage Mode.

Function

The matrix-vector product of a square sparse matrix or its transpose, is computed for a matrix stored in compressed-diagonal storage mode:

y<--Ax

y<--A^Tx

where:

A is a sparse matrix of order n, stored in compressed-diagonal storage mode in AD and LA, using the storage variation for either general or symmetric sparse matrices, as indicated by the iopt argument.

x and y are vectors of length n.

It is expressed as follows for y<--Ax:

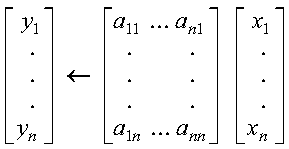
It is expressed as follows for y<--A^Tx:

If n is 0, no computation is performed; if nd is 0, output vector y is set to zero, because matrix A contains all zeros.

Error Conditions

Computational Errors

None

Input-Argument Errors

1. iopt <> 0 or 1
2. n < 0
3. lda <= 0
4. n > lda
5. trans <>  'N' or 'T'
6. nd < 0
7. LA(j) <= -n or LA(j) >= n, for any j = 1, n

Example 1

This example shows the matrix-vector product using trans = 'N', which is computed for the following sparse matrix A of order 6. The matrix is stored in compressed-matrix storage mode in arrays AD and LA using the storage variation for general sparse matrices, storing all nonzero diagonals. Matrix A is:

                     *                              *
                     | 4.0  0.0  7.0  0.0  0.0  0.0 |
                     | 3.0  4.0  0.0  2.0  0.0  0.0 |
                     | 0.0  2.0  4.0  0.0  4.0  0.0 |
                     | 0.0  0.0  7.0  4.0  0.0  1.0 |
                     | 1.0  0.0  0.0  3.0  4.0  0.0 |
                     | 1.0  1.0  0.0  0.0  3.0  4.0 |
                     *                              *

Call Statement and Input

           IOPT  N   ND  AD  LDA TRANS  LA   X   Y
            |    |   |   |    |    |    |    |   |
CALL DSDMX( 0  , 6 , 5 , AD , 6 , 'N' , LA , X , Y )

        *                         *
        | 4.0  0.0  0.0  0.0  7.0 |
        | 4.0  0.0  0.0  3.0  2.0 |
AD   =  | 4.0  0.0  0.0  2.0  4.0 |
        | 4.0  0.0  0.0  7.0  1.0 |
        | 4.0  0.0  1.0  3.0  0.0 |
        | 4.0  1.0  1.0  3.0  0.0 |
        *                         *

LA       =  (0, -5, -4, -1, 2)
X        =  (1.0, 2.0, 3.0, 4.0, 5.0, 6.0)

Output

Y        =  (25.0, 19.0, 36.0, 43.0, 33.0, 42.0)

Example 2

This example shows the matrix-vector product using trans = 'N', which is computed for the following sparse matrix A of order 6. The matrix is stored in compressed-matrix storage mode in arrays AD and LA using the storage variation for symmetric sparse matrices, storing the nonzero main diagonal and one of each of the unique nonzero diagonals. Matrix A is:

                  *                                    *
                  | 11.0   0.0  13.0   0.0  15.0   0.0 |
                  |  0.0  22.0   0.0  24.0   0.0  26.0 |
                  | 13.0   0.0  33.0   0.0  35.0   0.0 |
                  |  0.0  24.0   0.0  44.0   0.0  46.0 |
                  | 15.0   0.0  35.0   0.0  55.0   0.0 |
                  |  0.0  26.0   0.0  46.0   0.0  66.0 |
                  *                                    *

Call Statement and Input

           IOPT  N   ND  AD  LDA TRANS  LA   X   Y
            |    |   |   |    |    |    |    |   |
CALL DSDMX( 1  , 6 , 3 , AD , 6 , 'N' , LA , X , Y )

        *                  *
        | 11.0  13.0   0.0 |
        | 22.0  24.0   0.0 |
AD   =  | 33.0  35.0   0.0 |
        | 44.0  46.0   0.0 |
        | 55.0   0.0  15.0 |
        | 66.0   0.0  26.0 |
        *                  *

LA       =  (0, 2, -4)
X        =  (1.0, 2.0, 3.0, 4.0, 5.0, 6.0)

Output

Y        =  (125.0, 296.0, 287.0, 500.0, 395.0, 632.0)

Example 3

This example is the same as Example 1 except that it shows the matrix-vector product for the transpose of a matrix, using trans = 'T'. It is computed using the transpose of the following sparse matrix A of order 6, which is stored in compressed-matrix storage mode in arrays AD and LA, using the storage variation for general sparse matrices, storing all nonzero diagonals. It uses the same matrix A as in Example 1.

Call Statement and Input

           IOPT  N   ND  AD  LDA TRANS  LA   X   Y
            |    |   |   |    |    |    |    |   |
CALL DSDMX( 0  , 6 , 5 , AD , 6 , 'T' , LA , X , Y )

Output

Y        =  (21.0, 20.0, 47.0, 35.0, 50.0, 28.0)