Engineering and Scientific Subroutine Library for AIX Version 3 Release 3: Guide and Reference

SGETMO, DGETMO, CGETMO, and ZGETMO--General Matrix Transpose (Out-of-Place)

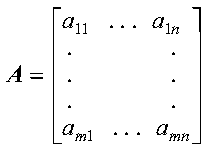
These subroutines transpose an m by n matrix A out of place, returning the result in matrix B:

B<--A^T

Table 82. Data Types

Syntax

On Entry

a

is the matrix A having m rows and n columns. Specified as: an lda by (at least) n array, containing numbers of the data type indicated in Table 82.

lda

is the leading dimension of the array specified for a. Specified as: a fullword integer; lda > 0 and lda >= m.

m

is the number of rows in matrix A and the number of columns in matrix B. Specified as: a fullword integer; m >= 0.

n

is the number of columns in matrix A and the number of rows in matrix B. Specified as: a fullword integer; n >= 0.

b

See On Return.

ldb

is the leading dimension of the array specified for b. Specified as: a fullword integer; ldb > 0 and ldb >= n.

On Return

b

is the matrix B having n rows and m columns, containing the results of the matrix transpose operation, A^T. Returned as: an ldb by (at least) m array, containing numbers of the data type indicated in Table 82.

Notes

1. The matrix B must have no common elements with matrix A; otherwise, results are unpredictable. See Concepts.
2. To achieve optimal performance in CGETMO, align the arrays specified for a and b on doubleword boundaries.

Function

Matrix A is transposed out of place; that is, the m rows and n columns in matrix A are stored in n rows and m columns of matrix B. For matrix A with elements a_ij, where i = 1, m and j = 1, n, the out-of-place transpose is expressed as b_ji = a_ij for i = 1, m and j = 1, n.

For the following input matrix A:

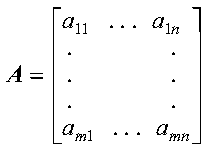
the out-of-place matrix transpose operation B<--A^T is expressed as:

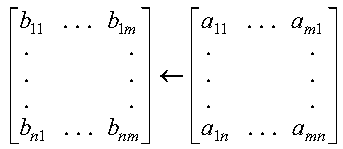
If m or n is 0, no computation is performed.

Error Conditions

Computational Errors

None

Input-Argument Errors

1. m < 0 or m > lda
2. n < 0 or n > ldb
3. lda <= 0
4. ldb <= 0

Example 1

This example shows an out-of-place matrix transpose of matrix A, having 5 rows and 4 columns, with the result going into matrix B.

Call Statement and Input

               A     LDA   M   N     B     LDB
               |      |    |   |     |      |
CALL SGETMO( A(2,3) , 10 , 5 , 4 , B(2,2) , 6 )

        *                                *
        | .  .   .     .     .     .   . |
        | .  .  1.0   6.0  11.0  16.0  . |
        | .  .  2.0   7.0  12.0  17.0  . |
        | .  .  3.0   8.0  13.0  18.0  . |
A    =  | .  .  4.0   9.0  14.0  19.0  . |
        | .  .  5.0  10.0  15.0  20.0  . |
        | .  .   .     .     .     .   . |
        | .  .   .     .     .     .   . |
        | .  .   .     .     .     .   . |
        | .  .   .     .     .     .   . |
        *                                *

Output

        *                                    *
        | .    .     .     .     .     .   . |
        | .   1.0   2.0   3.0   4.0   5.0  . |
B    =  | .   6.0   7.0   8.0   9.0  10.0  . |
        | .  11.0  12.0  13.0  14.0  15.0  . |
        | .  16.0  17.0  18.0  19.0  20.0  . |
        | .    .     .     .     .     .   . |
        *                                    *

Example 2

This example uses the same input matrix A as in Example 1 to show that transposes can be achieved in the same array as long as the input and output data do not overlap. On output, the input data is not overwritten in the array.

Call Statement and Input

               A     LDA   M   N     B     LDB
               |      |    |   |     |      |
CALL SGETMO( A(2,3) , 10 , 5 , 4 , A(7,1) , 10 )

        *                                       *
        |   .     .     .     .     .     .   . |
        |   .     .    1.0   6.0  11.0  16.0  . |
        |   .     .    2.0   7.0  12.0  17.0  . |
        |   .     .    3.0   8.0  13.0  18.0  . |
A    =  |   .     .    4.0   9.0  14.0  19.0  . |
        |   .     .    5.0  10.0  15.0  20.0  . |
        |  1.0   2.0   3.0   4.0   5.0    .   . |
        |  6.0   7.0   8.0   9.0  10.0    .   . |
        | 11.0  12.0  13.0  14.0  15.0    .   . |
        | 16.0  17.0  18.0  19.0  20.0    .   . |
        *                                       *