Engineering and Scientific Subroutine Library for AIX Version 3 Release 3: Guide and Reference

SGETMI, DGETMI, CGETMI, and ZGETMI--General Matrix Transpose (In-Place)

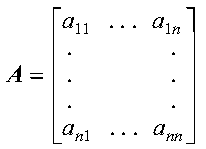
These subroutines transpose an n by n matrix A in place--that is, in matrix A:

A<--A^T

Table 81. Data Types

Syntax

On Entry

a

is the matrix A having n rows and n columns. Specified as: an lda by (at least) n array, containing numbers of the data type indicated in Table 81.

lda

is the leading dimension of the array specified for a. Specified as: a fullword integer; lda > 0 and lda >= n.

n

is the number of rows and columns in matrix A. Specified as: a fullword integer; n >= 0.

On Return

a

is the n by n matrix A^T, containing the results of the matrix transpose operation Returned as: an lda by (at least) n array, containing numbers of the data type indicated in Table 81.

Notes

1. To achieve optimal performance in these subroutines, specify an even value for lda. An odd value may degrade performance.
2. To achieve optimal performance in CGETMI, align the array specified for a on a doubleword boundary.

Function

Matrix A is transposed in place; that is, the n rows and n columns in matrix A are exchanged. For matrix A with elements a_ij, where i, j = 1, n, the in-place transpose is expressed as a_ji = a_ij for i, j = 1, n.

For the following input matrix A:

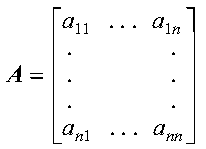
the in-place matrix transpose operation A<--A^T is expressed as:

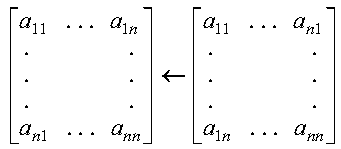
If n is 0, no computation is performed.

Error Conditions

Computational Errors

None

Input-Argument Errors

1. n < 0 or n > lda
2. lda <= 0

Example

This example shows an in-place matrix transpose of matrix A having 5 rows and 5 columns.

Call Statement and Input

               A     LDA   N
               |      |    |
CALL SGETMI( A(2,3) , 10 , 5 )

        *                                    *
        | .   .   .     .     .     .     .  |
        | .   .  1.0   6.0  11.0  16.0  21.0 |
        | .   .  2.0   7.0  12.0  17.0  22.0 |
        | .   .  3.0   8.0  13.0  18.0  23.0 |
A    =  | .   .  4.0   9.0  14.0  19.0  24.0 |
        | .   .  5.0  10.0  15.0  20.0  25.0 |
        | .   .   .     .     .     .     .  |
        | .   .   .     .     .     .     .  |
        | .   .   .     .     .     .     .  |
        | .   .   .     .     .     .     .  |
        *                                    *

Output

        *                                     *
        | .   .    .     .     .     .     .  |
        | .   .   1.0   2.0   3.0   4.0   5.0 |
        | .   .   6.0   7.0   8.0   9.0  10.0 |
        | .   .  11.0  12.0  13.0  14.0  15.0 |
A    =  | .   .  16.0  17.0  18.0  19.0  20.0 |
        | .   .  21.0  22.0  23.0  24.0  25.0 |
        | .   .    .     .     .     .     .  |
        | .   .    .     .     .     .     .  |
        | .   .    .     .     .     .     .  |
        | .   .    .     .     .     .     .  |
        *                                     *