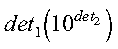Engineering and Scientific Subroutine Library for AIX Version 3 Release 3: Guide and Reference
|These subroutines find the inverse of positive definite real symmetric matrix
A using Cholesky factorization, where:
- For SPPICD and DPPICD, A is stored in lower-packed storage
mode.
- |For SPOICD, DPOICD, SPOTRI, and DPOTRI, A is stored in
|upper or lower storage mode.
|Subroutines SPPICD, DPPICD, SPOICD, and DPOICD also find the
|reciprocal of the condition number and the determinant of matrix
|A.
Table 101. Data Types
| A, aux, rcond, det
| Subroutine
|
| Short-precision real
| SPPICD, SPOICD, and SPOTRI
|
| Long-precision real
| DPPICD, DPOICD, and DPOTRI
|
- Note:
- |If you call subroutines SPPICD, SPOICD, DPPICD, and DPOICD with
|iopt = 4, the input must be the output from the factorization
|subroutines SPPF, DPPF, SPOF/SPOFCD, or DPOF/DPOFCD, respectively, where
|Cholesky factorization was performed.
|For SPOTRI and DPOTRI, the input |must be the output from the factorization subroutines SPOTRF or DPOTRF,
|respectively.
|
| Fortran
| CALL SPPICD | DPPICD (ap, n, iopt,
rcond, det, aux, naux)
CALL SPOICD | DPOICD (uplo, a, lda, n,
iopt, rcond, det, aux, naux)
CALL SPOTRI | DPOTRI (uplo, n, a,
lda, info)
|
| C and C++
| sppicd | dppicd (ap, n, iopt, rcond,
det, aux, naux);
spoicd | dpoicd (uplo, a, lda, n,
iopt, rcond, det, aux,
naux);
spotri | dpotri (uplo, n, a,
lda, info);
|
| PL/I
| CALL SPPICD | DPPICD (ap, n, iopt,
rcond, det, aux, naux);
CALL SPOICD | DPOICD (uplo, a, lda, n,
iopt, rcond, det, aux,
naux);
CALL SPOTRI | DPOTRI (uplo, n, a,
lda, info);
|
- uplo
- indicates whether matrix A is stored in upper or lower storage
mode, where:
If uplo = 'U', A is stored in upper
storage mode.
If uplo = 'L', A is stored in lower
storage mode.
Specified as: a single character. It must be 'U' or
'L'.
- ap
- is the array, referred to as AP, where:
If iopt = 0, 1, 2, or 3, then AP contains the
positive definite real symmetric matrix A, whose inverse, condition
number reciprocal, and determinant are computed, where matrix A is
stored in lower-packed storage mode.
If iopt = 4, then AP contains the transformed
matrix A of order n, resulting from the Cholesky
factorization performed in a previous call to SPPF or DPPF, respectively,
whose inverse is computed.
Specified as: a one-dimensional array of (at least) length
n(n+1)/2, containing numbers of the data type indicated in Table 101.
- a
- has the following meaning, where:
- |For SPPICD, DPPICD, SPOICD, and DPOICD:
-
If iopt = 0, 1, 2, or 3, it is the positive definite real
symmetric matrix A, whose inverse, condition number reciprocal, and
determinant are computed, where matrix A is stored in upper or
lower storage mode.
If iopt = 4, it is the transformed matrix A of
order n, containing results of the factorization from a previous call
to SPOF/SPOFCD or DPOF/DPOFCD, respectively, whose inverse is computed.
|
- |For SPOTRI and DPOTRI:
-
|It is the transformed matrix A of order n, containing
|results of the factorization from a previous call to SPOTRF or DPOTRF,
|respectively, whose inverse is computed.
Specified as: an |lda by (at least) n array, containing numbers of the data type
indicated in Table 101.
- lda
- is the leading dimension of the array specified for a.
Specified as: a fullword integer; lda > 0 and
lda >= n.
- n
- is the order n of matrix A. Specified as:
a fullword integer; n >= 0.
- iopt
- indicates the type of computation to be performed, where:
If iopt = 0, the inverse is computed for matrix
A.
If iopt = 1, the inverse and the reciprocal of the
condition number are computed for matrix A.
If iopt = 2, the inverse and the determinant are computed
for matrix A.
If iopt = 3, the inverse, the reciprocal of the condition
number, and the determinant are computed for matrix A.
If iopt = 4, the inverse is computed for the (Cholesky)
factored matrix A.
Specified as: a fullword integer; iopt = 0, 1,
2, 3, or 4.
- rcond
- See On Return.
- det
- See On Return.
- aux
- has the following meaning:
If naux = 0 and error 2015 is unrecoverable, aux
is ignored.
Otherwise, it is the storage work area used by this subroutine. Its
size is specified by naux. Specified as: an area of
storage, containing numbers of the data type indicated in Table 101.
- naux
- is the size of the work area specified by aux--that is, the
number of elements in aux. Specified as: a fullword
integer, where:
If naux = 0 and error 2015 is unrecoverable, SPPICD,
DPPICD, SPOICD, |and DPOICD dynamically allocate the work area used by the
subroutine. The work area is deallocated before control is returned to
the calling program.
Otherwise, naux >= n.
- |info
- |See On Return.
- ap
- is the resulting array, referred to as AP, containing the
inverse of the matrix in lower-packed storage mode. Returned as:
a one-dimensional array of (at least) length n(n+1)/2,
containing numbers of the data type indicated in Table 101.
- a
- is the transformed matrix A of order n, containing the
inverse of the matrix in upper or lower storage mode. Returned
as: a two-dimensional array, containing numbers of the data type
indicated in Table 101.
- rcond
- is the reciprocal of the condition number, rcond, of matrix
A. Returned as: a real number of the data type
indicated in Table 101; rcond >= 0.
- det
- is the vector det, containing the two components
det1 and det2 of the determinant of
matrix A. The determinant is:
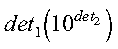
where 1 <= det1 < 10.
Returned as: an array of length 2, containing numbers of the data type
indicated in Table 101.
- |info
- |has the following meaning:
|If info = 0, the inverse completed
|successfully.
|If info > 0, info is set equal to the
|first i, where Aii is zero; the matrix is
|not positive definite, and its inverse could not be completed.
|Specified as: a fullword integer;
|info >= 0.
- |In your C program, the arguments info and |rcond must be passed by reference.
- |For SPPICD, DPPICD, SPOICD, and DPOICD, when you specify
|iopt = 4, you must do the following:
|
- |For SPPICD and DPPICD, use Cholesky factorization in the previous call to
|SPPF or DPPF, respectively.
- |For SPOICD and DPOICD, specify the same storage mode for matrix
|A that was specified in the previous call to SPOF/SPOFCD or
|DPOF/DPOFCD, |respectively.
|
- |The scalar data specified for input arguments uplo,
lda, and n for these subroutines must be the same as the
corresponding input arguments specified for |SPOF/SPOFCD/SPOTRF and DPOF/DPOFCD/DPOTRF, respectively.
- All subroutines accept lowercase letters for the uplo |argument.
- |SPPICD and DPPICD in some cases utilize algorithms based on recursive
packed storage format. (See references [52], [66], and [67]).
- |The way _POTRI subroutines handle computational errors differs from
|LAPACK. These subroutines use the info argument to provide
|information about the computational error, like LAPACK, but also provide an
|error message.
- |On both input and output, matrix A conforms to LAPACK
|format.
- For a description of how a positive definite symmetric matrix is stored in
lower-packed storage mode in an array, see Symmetric Matrix. For a description of how a positive definite
symmetric matrix is stored in upper or lower storage mode, see Positive Definite or Negative Definite Symmetric Matrix.
- You have the option of having the minimum required value for naux
dynamically returned to your program. For details, see Using Auxiliary Storage in ESSL.
These subroutines perform the following function:
- |SPPICD, DPPICD, SPOICD, and DPOICD
-
|Find the inverse, the reciprocal of the condition number, and the
determinant of positive definite symmetric matrix A using Cholesky
factorization, where:
- A-1 is the inverse of matrix A,
where
AA-1 = A-1A = I,
and I is the identity matrix.
- 1/(||A||1)(||A-1||1)
is the reciprocal of the condition number, where
||A||1 is the one-norm of matrix
A.
- |A| is the determinant of matrix A, where
|A| is expressed as:
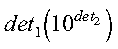
The iopt argument is used to determine the combination of output
items produced by this subroutine: the inverse, the reciprocal of the
condition number, and the determinant.
|
- |SPOTRI and DPOTRI
- |Find the inverse of positive definite symmetric matrix
|A.
If n is 0, no computation is performed. See references
[36], [38], and [44].
- Error 2015 is unrecoverable, naux = 0, and unable to
allocate work area.
- Unable to allocate internal work area.
- |For SPPICD, DPPICD, SPOICD, and DPOICD:
-
Matrix A is not positive definite.
- These subroutines do not perform the inverse, determinant, and reciprocal
of the condition number computations.
- For iopt = 1, 2, or 3, the leading minor of order
i has a nonpositive determinant. The order i is
identified in the computational error |message.
- i can be determined at run time by using the ESSL error-handling
facilities. To obtain this information, you must use ERRSET to change
the number of allowable errors for error code 2115 in the error option
table; otherwise, the default value causes your program to
terminate. If your program is not terminated, the return code is set to
2. For details, see What Can You Do about ESSL Computational Errors?.
|The inverse of matrix A could not be computed.
|
- |For iopt = 4, for _POICD and _PPICD, one or more of the
|diagonal elements of the factored matrix A are zero.
|i is the first diagonal element that is found to be exactly zero and
|is identified in the computational error message. If one or more of the
|diagonal elements of the factored matrix A are negative, the
|results are unpredictable.
- |i can be determined at run time by using the ESSL error-handling
|facilities. To obtain this information, you must use ERRSET to change
|the number of allowable errors for error code 2150 in the error option
|table; otherwise, the default value causes your program to
|terminate. If your program is not terminated, the return code is set to
|3. For details, see What Can You Do about ESSL Computational Errors?.
|
|
- |For SPOTRI and DPOTRI:
-
|The inverse of matrix A could not be computed.
|
- |One or more of the diagonal elements of the factored matrix A
|are zero. The first diagonal element that is found to be exactly zero
|is identified in the computational error message and returned in
|info. If one or more of the diagonal elements of the factored
|matrix A are negative, the results are unpredictable.
- |The computational error message may occur multiple times with processing
|continuing after each error because the default for the number of allowable
|errors for error code 2151 is set to be unlimited in the ESSL error option
|table.
|
- uplo <> 'U' or 'L'
- n < 0
- lda <= 0
- lda < n
- iopt <> 0, 1, 2, 3, or 4
- Error 2015 is recoverable or naux<>0, and naux is
too small--that is, less than the minimum required value. Return
code 1 is returned if error 2015 is recoverable.
This example uses SPPICD to compute the inverse, reciprocal of the
condition number, and determinant of matrix A. Where
A is:
* *
| 1.0 1.0 1.0 1.0 1.0 1.0 1.0 1.0 1.0 |
| 1.0 2.0 2.0 2.0 2.0 2.0 2.0 2.0 2.0 |
| 1.0 2.0 3.0 3.0 3.0 3.0 3.0 3.0 3.0 |
| 1.0 2.0 3.0 4.0 4.0 4.0 4.0 4.0 4.0 |
| 1.0 2.0 3.0 4.0 5.0 5.0 5.0 5.0 5.0 |
| 1.0 2.0 3.0 4.0 5.0 6.0 6.0 6.0 6.0 |
| 1.0 2.0 3.0 4.0 5.0 6.0 7.0 7.0 7.0 |
| 1.0 2.0 3.0 4.0 5.0 6.0 7.0 8.0 8.0 |
| 1.0 2.0 3.0 4.0 5.0 6.0 7.0 8.0 9.0 |
* *
The values used to compute the reciprocal of the condition number in this
example are obtained with the following values:
- ||A||1 = max(9.0, 17.0,
24.0, 30.0, 35.0, 39.0, 42.0, 44.0,
45.0) = 45.0
- ||A-1||1 = 4.0
On output, the value in det, |A|, is equal to 1, and
RCOND = 1/180.
- Note:
- The AP arrays are formatted in a triangular arrangement for
readability; however, they are stored in lower-packed storage
mode.
AP N IOPT RCOND DET AUX NAUX
| | | | | | |
CALL SPPICD( AP , 9 , 3 , RCOND , DET , AUX , 9 )
AP = (1.0, 1.0, 1.0, 1.0, 1.0, 1.0, 1.0, 1.0, 1.0,
2.0, 2.0, 2.0, 2.0, 2.0, 2.0, 2.0, 2.0,
3.0, 3.0, 3.0, 3.0, 3.0, 3.0, 3.0,
4.0, 4.0, 4.0, 4.0, 4.0, 4.0,
5.0, 5.0, 5.0, 5.0, 5.0,
6.0, 6.0, 6.0, 6.0,
7.0, 7.0, 7.0,
8.0, 8.0,
9.0)
AP = (2.0, -1.0, 0.0, 0.0, 0.0, 0.0, 0.0, 0.0, 0.0,
2.0, -1.0, 0.0, 0.0, 0.0, 0.0, 0.0, 0.0,
2.0, -1.0, 0.0, 0.0, 0.0, 0.0, 0.0,
2.0, -1.0, 0.0, 0.0, 0.0, 0.0,
2.0, -1.0, 0.0, 0.0, 0.0,
2.0, -1.0, 0.0, 0.0,
2.0, -1.0, 0.0,
2.0, -1.0,
1.0)
RCOND = 0.005556
DET = (1.0, 0.0)
This example uses SPPICD to compute the inverse of matrix A,
where iopt = 4, and matrix A is the transformed
matrix factored in Example 1 by SPPF.
- Note:
- The AP arrays are formatted in a triangular arrangement for
readability; however, they are stored in lower-packed storage
mode.
AP N IOPT RCOND DET AUX NAUX
| | | | | | |
CALL SPPICD(AP , 9 , 4 , RCOND , DET , AUX , 9)
AP =(same as output AP in Example 2 for SPPF)
AP = (2.0, -1.0, 0.0, 0.0, 0.0, 0.0, 0.0, 0.0, 0.0,
2.0, -1.0, 0.0, 0.0, 0.0, 0.0, 0.0, 0.0,
2.0, -1.0, 0.0, 0.0, 0.0, 0.0, 0.0,
2.0, -1.0, 0.0, 0.0, 0.0, 0.0,
2.0, -1.0, 0.0, 0.0, 0.0,
2.0, -1.0, 0.0, 0.0,
2.0, -1.0, 0.0,
2.0, -1.0,
1.0)
This example uses SPOICD to compute the inverse, reciprocal of the
condition number, and determinant of the same matrix A used in
Example 1; however, matrix A is stored in upper storage mode
in this example.
The values used to compute the reciprocal of the condition number in this
example are obtained with the following values:
- ||A||1 = max(9.0,
17.0, 24.0, 30.0, 35.0, 39.0, 42.0,
44.0, 45.0) = 45.0
- ||A-1||1 = 4.0
On output, the value in det, |A|, is equal to 1, and
RCOND = 1/180.
UPLO A LDA N IOPT RCOND DET AUX NAUX
| | | | | | | | |
CALL SPOICD( 'U' , A , 9 , 9 , 3 , RCOND , DET , AUX , 9 )
* *
| 1.0 1.0 1.0 1.0 1.0 1.0 1.0 1.0 1.0 |
| . 2.0 2.0 2.0 2.0 2.0 2.0 2.0 2.0 |
| . . 3.0 3.0 3.0 3.0 3.0 3.0 3.0 |
| . . . 4.0 4.0 4.0 4.0 4.0 4.0 |
A = | . . . . 5.0 5.0 5.0 5.0 5.0 |
| . . . . . 6.0 6.0 6.0 6.0 |
| . . . . . . 7.0 7.0 7.0 |
| . . . . . . . 8.0 8.0 |
| . . . . . . . . 9.0 |
* *
* *
| 2.0 -1.0 0.0 0.0 0.0 0.0 0.0 0.0 0.0 |
| . 2.0 -1.0 0.0 0.0 0.0 0.0 0.0 0.0 |
| . . 2.0 -1.0 0.0 0.0 0.0 0.0 0.0 |
| . . . 2.0 -1.0 0.0 0.0 0.0 0.0 |
A = | . . . . 2.0 -1.0 0.0 0.0 0.0 |
| . . . . . 2.0 -1.0 0.0 0.0 |
| . . . . . . 2.0 -1.0 0.0 |
| . . . . . . . 2.0 -1.0 |
| . . . . . . . . 1.0 |
* *
RCOND = 0.005555556
DET = (1.0, 0.0)
This example uses SPOICD or SPOTRI to compute the inverse of matrix
A, where iopt = 4, and matrix A is the
transformed matrix factored by |SPOF or SPOTRF in Example 1.
UPLO A LDA N IOPT RCOND DET AUX NAUX
| | | | | | | | |
CALL SPOICD( 'U' , A , 9 , 9 , 4 , RCOND , DET , AUX , 9 )
|or
| UPLO N A LDA INFO
| | | | | |
|CALL SPOTRI( 'U' , 9 , A , 9 , INFO )
A =(same as output A in Example 4 for SPOF |or SPOTRF)
* *
| 2.0 -1.0 0.0 0.0 0.0 0.0 0.0 0.0 0.0 |
| . 2.0 -1.0 0.0 0.0 0.0 0.0 0.0 0.0 |
| . . 2.0 -1.0 0.0 0.0 0.0 0.0 0.0 |
| . . . 2.0 -1.0 0.0 0.0 0.0 0.0 |
A = | . . . . 2.0 -1.0 0.0 0.0 0.0 |
| . . . . . 2.0 -1.0 0.0 0.0 |
| . . . . . . 2.0 -1.0 0.0 |
| . . . . . . . 2.0 -1.0 |
| . . . . . . . . 1.0 |
* *
|INFO = 0
[ Top of Page | Previous Page | Next Page | Table of Contents | Index ]