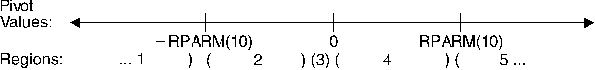Engineering and Scientific Subroutine Library for AIX Version 3 Release 3: Guide and Reference

DGKFS--General Sparse Matrix or Its Transpose Factorization, Determinant, and Solve Using Skyline Storage Mode

This subroutine can perform either or both of the following functions for general sparse matrix A, stored in skyline storage mode, and for vectors x and b:

Factor A and, optionally, compute the determinant of A.
Solve the system Ax = b or A^Tx = b using the results of the factorization of matrix A, produced on this call or a preceding call to this subroutine.

You also have the choice of using profile-in or diagonal-out skyline storage mode for A on input or output.

Note:: The input to the solve performed by this subroutine must be the output from the factorization performed by this subroutine.

Syntax

Fortran	CALL DGKFS (`n`, `au`, `nu`, `idu`, `al`, `nl`, `idl`, `iparm`, `rparm`, `aux`, `naux`, `bx`, `ldbx`, `mbx`)
C and C++	dgkfs (`n`, `au`, `nu`, `idu`, `al`, `nl`, `idl`, `iparm`, `rparm`, `aux`, `naux`, `bx`, `ldbx`, `mbx`);
PL/I	CALL DGKFS (`n`, `au`, `nu`, `idu`, `al`, `nl`, `idl`, `iparm`, `rparm`, `aux`, `naux`, `bx`, `ldbx`, `mbx`);

On Entry

n

is the order of general sparse matrix A. Specified as: a fullword integer; n >= 0.

au

is the array, referred to as AU, containing one of three forms of the upper triangular part of general sparse matrix A, depending on the type of computation performed, where:

If you are doing a factor and solve or a factor only, and if IPARM(3) = 0, then AU contains the unfactored upper triangle of general sparse matrix A.
If you are doing a factor only, and if IPARM(3) > 0, then AU contains the partially factored upper triangle of general sparse matrix A. The first IPARM(3) columns in the upper triangle of A are already factored. The remaining columns are factored in this computation.
If you are doing a solve only, then AU contains the factored upper triangle of general sparse matrix A, produced by a preceding call to this subroutine.

In each case:

If IPARM(4) = 0, diagonal-out skyline storage mode is used for A.

If IPARM(4) = 1, profile-in skyline storage mode is used for A.

Specified as: a one-dimensional array of (at least) length nu, containing long-precision real numbers.

nu

is the length of array AU. Specified as: a fullword integer; nu >= 0 and nu >= (IDU(n+1)-1).

idu

is the array, referred to as IDU, containing the relative positions of the diagonal elements of matrix A (in one of its three forms) in array AU. Specified as: a one-dimensional array of (at least) length n+1, containing fullword integers.

al

is the array, referred to as AL, containing one of three forms of the lower triangular part of general sparse matrix A, depending on the type of computation performed, where:

If you are doing a factor and solve or a factor only, and if IPARM(3) = 0, then AL contains the unfactored lower triangle of general sparse matrix A.
If you are doing a factor only, and if IPARM(3) > 0, then AL contains the partially factored lower triangle of general sparse matrix A. The first IPARM(3) rows in the lower triangle of A are already factored. The remaining rows are factored in this computation.
If you are doing a solve only, then AL contains the factored lower triangle of general sparse matrix A, produced by a preceding call to this subroutine.

Note:: In all these cases, entries in AL for diagonal elements of A are not assumed to have meaningful values.

In each case:

If IPARM(4) = 0, diagonal-out skyline storage mode is used for A.

If IPARM(4) = 1, profile-in skyline storage mode is used for A.

Specified as: a one-dimensional array of (at least) length nl, containing long-precision real numbers.

nl

is the length of array AL. Specified as: a fullword integer; nl >= 0 and nl >= (IDL(n+1)-1).

idl

is the array, referred to as IDL, containing the relative positions of the diagonal elements of matrix A (in one of its three forms) in array AL. Specified as: a one-dimensional array of (at least) length n+1, containing fullword integers.

iparm

is an array of parameters, IPARM(i), where:

IPARM(1) indicates whether certain default values for iparm and rparm are used by this subroutine, where:
If IPARM(1) = 0, the following default values are used. For restrictions, see Notes.

IPARM(2) = 0
IPARM(3) = 0
IPARM(4) = 0
IPARM(5) = 0
IPARM(10) = 0
IPARM(11) = -1
IPARM(12) = -1
IPARM(13) = -1
IPARM(14) = -1
IPARM(15) = 0
RPARM(10) = 10^-12

If IPARM(1) = 1, the default values are not used.
IPARM(2) indicates the type of computation performed by this subroutine. The following table gives the IPARM(2) values for each variation:

Type of Computation Ax = b Ax = b and Determinant(A) A^Tx = b A^Tx = b and Determinant(A)
Factor and Solve 0 10 100 110
Factor Only 1 11 N/A N/A
Solve Only 2 N/A 102 N/A
IPARM(3) indicates whether a full or partial factorization is performed on matrix A, where:
If IPARM(3) = 0, and:

If you are doing a factor and solve or a factor only, then a full factorization is performed for matrix A on rows and columns 1 through n.
If you are doing a solve only, this argument has no effect on the computation, but must be set to 0.

If IPARM(3) > 0, and you are doing a factor only, then a partial factorization is performed on matrix A. Rows 1 through IPARM(3) of columns 1 through IPARM(3) in matrix A must be in factored form from a preceding call to this subroutine. The factorization is performed on rows IPARM(3)+1 through n and columns IPARM(3)+1 through n. For an illustration, see Notes.
IPARM(4) indicates the input storage mode used for matrix A. This determines the arrangement of data in arrays AU, IDU, AL, and IDL on input, where:
If IPARM(4) = 0, diagonal-out skyline storage mode is used.
If IPARM(4) = 1, profile-in skyline storage mode is used.
IPARM(5) indicates the output storage mode used for matrix A. This determines the arrangement of data in arrays AU, IDU, AL, and IDL on output, where:
If IPARM(5) = 0, diagonal-out skyline storage mode is used.
If IPARM(5) = 1, profile-in skyline storage mode is used.
IPARM(6) through IPARM(9) are reserved.
IPARM(10) has the following meaning, where:
If you are doing a factor and solve or a factor only, then IPARM(10) indicates whether certain default values for iparm and rparm are used by this subroutine, where:

If IPARM(10) = 0, the following default values are used. For restrictions, see Notes.

IPARM(11) = -1
IPARM(12) = -1
IPARM(13) = -1
IPARM(14) = -1
IPARM(15) = 0
RPARM(10) = 10^-12

If IPARM(10) = 1, the default values are not used.

If you are doing a solve only, this argument is not used.
IPARM(11) through IPARM(15) have the following meaning, where:
If you are doing a factor and solve or a factor only, then IPARM(11) through IPARM(15) control the type of processing to apply to pivot elements occurring in regions 1 through 5, respectively. The pivot elements are u_kk for k = 1, n when doing a full factorization, and they are k = IPARM(3)+1, n when doing a partial factorization. The region in which a pivot element falls depends on the sign and magnitude of the pivot element. The regions are determined by RPARM(10). For a description of the regions and associated pivot values, see Notes. For each region i for i = 1,5, where the pivot occurs in region i, the processing applied to the pivot element is determined by IPARM(10+i), where:

If IPARM(10+i) = -1, the pivot element is trapped and computational error 2126 is generated. See Error Conditions.
If IPARM(10+i) = 0, for i = 1, 2, 4, and 5, processing continues normally.
Note:
A value of 0 is not permitted for region 3, because if processing continues, a divide-by-zero exception occurs.

If IPARM(10+i) = 1, the pivot element is replaced with the value in RPARM(10+i), and processing continues normally.

If you are doing a solve only, these arguments are not used.
IPARM(16) through IPARM(25), see On Return.

Type of Computation	Ax = b	Ax = b and Determinant(A)	A^Tx = b	A^Tx = b and Determinant(A)
Factor and Solve	0	10	100	110
Factor Only	1	11	N/A	N/A
Solve Only	2	N/A	102	N/A

Specified as: a one-dimensional array of (at least) length 25, containing fullword integers, where:

IPARM(1) = 0 or 1

IPARM(2) = 0, 1, 2, 10, 11, 100, 102, or 110

If IPARM(2) = 0, 2, 10, 100, 102, or 110, then IPARM(3) = 0

If IPARM(2) = 1 or 11, then 0 <= IPARM(3) <= n

IPARM(4), IPARM(5) = 0 or 1

If IPARM(2) = 0, 1, 10, 11, 100, or 110, then:

IPARM(10) = 0 or 1

IPARM(11), IPARM(12) = -1, 0, or 1

IPARM(13) = -1 or 1

IPARM(14), IPARM(15) = -1, 0, or 1

rparm

is an array of parameters, RPARM(i), where:

RPARM(1) through RPARM(9) are reserved.
RPARM(10) has the following meaning, where:
If you are doing a factor and solve or a factor only, RPARM(10) is the tolerance value for small pivots. This sets the bounds for the pivot regions, where pivots are processed according to the options you specify for the five regions in IPARM(11) through IPARM(15), respectively. The suggested value is 10^-15 <= IPARM(10) <= 1.

If you are doing a solve only, this argument is not used.
RPARM(11) through RPARM(15) have the following meaning, where:
If you are doing a factor and solve or a factor only, RPARM(11) through RPARM(15) are the fix-up values to use for the pivots in regions 1 through 5, respectively. For each RPARM(10+i) for i = 1,5, where the pivot occurs in region i:

If IPARM(10+i) = 1, the pivot is replaced with RPARM(10+i), where |RPARM(10+i)| should be a sufficiently large nonzero value to avoid overflow when calculating the reciprocal of the pivot. The suggested value is 10^-15 <= |RPARM(10+i)| <= 1.
If IPARM(10+i) <> 1, RPARM(10+i) is not used.

If you are doing a solve only, these arguments are not used.
RPARM(16) through RPARM(25), see On Return.

Specified as: a one-dimensional array of (at least) length 25, containing long-precision real numbers, where if IPARM(2) = 0, 1, 10, 11, 100, or 110, then:

RPARM(10) >= 0.0

RPARM(11) through RPARM(15) <> 0.0

aux

has the following meaning:

If naux = 0 and error 2015 is unrecoverable, aux is ignored.

Otherwise, it is the storage work area used by this subroutine. Its size is specified by naux.

Specified as: an area of storage, containing long-precision real numbers.

naux

is the size of the work area specified by aux--that is, the number of elements in aux. Specified as: a fullword integer, where:

If naux = 0 and error 2015 is unrecoverable, DGKFS dynamically allocates the work area used by this subroutine. The work area is deallocated before control is returned to the calling program.

Otherwise,

If you are doing a factor only, use naux >= 5n.

If you are doing a factor and solve or a solve only, use naux >= 5n+4mbx.

bx

has the following meaning, where:

If you are doing a factor and solve or a solve only, bx is the array, containing the mbx right-hand side vectors b of the system Ax = b or A^Tx = b. Each vector b is length n and is stored in the corresponding column of the array.

If you are doing a factor only, this argument is not used in the computation.

Specified as: an ldbx by (at least) mbx array, containing long-precision real numbers.

ldbx

has the following meaning, where:

If you are doing a factor and solve or a solve only, ldbx is the leading dimension of the array specified for bx.

If you are doing a factor only, this argument is not used in the computation.

Specified as: a fullword integer; ldbx >= n and:

If mbx <> 0, then ldbx > 0.

If mbx = 0, then ldbx >= 0.

mbx

has the following meaning, where:

If you are doing a factor and solve or a solve only, mbx is the number of right-hand side vectors, b, in the array specified for bx.

If you are doing a factor only, this argument is not used in the computation.

Specified as: a fullword integer; mbx >= 0.

On Return

au

is the array, referred to as AU, containing the upper triangular part of the LU factored form of general sparse matrix A, where:

If IPARM(5) = 0, diagonal-out skyline storage mode is used for A.

If IPARM(5) = 1, profile-in skyline storage mode is used for A.

(If mbx = 0 and you are doing a solve only, then au is unchanged on output.) Returned as: a one-dimensional array of (at least) length nu, containing long-precision real numbers.

idu

is the array, referred to as IDU, containing the relative positions of the diagonal elements of the factored output matrix A in array AU. (If mbx = 0 and you are doing a solve only, then idu is unchanged on output.) Returned as: a one-dimensional array of (at least) length n+1, containing fullword integers.

al

is the array, referred to as AL, containing the lower triangular part of the LU factored form of general sparse matrix A, where:

If IPARM(5) = 0, diagonal-out skyline storage mode is used for A.

If IPARM(5) = 1, profile-in skyline storage mode is used for A.

Note:: You should assume that entries in AL for diagonal elements of A do not have meaningful values.

(If mbx = 0 and you are doing a solve only, then al is unchanged on output.) Returned as: a one-dimensional array of (at least) length nl, containing long-precision real numbers.

idl

is the array, referred to as IDL, containing the relative positions of the diagonal elements of the factored output matrix A in array AL. (If mbx = 0 and you are doing a solve only, then idl is unchanged on output.) Returned as: a one-dimensional array of (at least) length n+1, containing fullword integers.

iparm

is an array of parameters, IPARM(i), where:

IPARM(1) through IPARM(15) are unchanged.
IPARM(16) has the following meaning, where:
If you are doing a factor and solve or a factor only, and:

If IPARM(16) = -1, your factorization did not complete successfully, resulting in computational error 2126.
If IPARM(16) > 0, it is the row number k, in which the maximum absolute value of the ratio a_kk/u_kk occurred, where:

If IPARM(3) = 0, k can be any of the rows, 1 through n, in the full factorization.
If IPARM(3) > 0, k can be any of the rows, IPARM(3)+1 through n, in the partial factorization.

If you are doing a solve only, this argument is not used in the computation and is unchanged.
IPARM(17) through IPARM(20) are reserved.
IPARM(21) through IPARM(25) have the following meaning, where:
If you are doing a factor and solve or a factor only, IPARM(21) through IPARM(25) have the following meanings for each region i for i = 1,5, respectively:

If IPARM(20+i) = -1, your factorization did not complete successfully, resulting in computational error 2126.
If IPARM(20+i) >= 0, it is the number of pivots in region i for the columns that were factored in matrix A, where:

If IPARM(3) = 0, columns 1 through n were factored in the full factorization.
If IPARM(3) > 0, columns IPARM(3)+1 through n were factored in the partial factorization.

If you are doing a solve only, these arguments are not used in the computation and are unchanged.

Returned as: a one-dimensional array of (at least) length 25, containing fullword integers.

rparm

is an array of parameters, RPARM(i), where:

RPARM(1) through RPARM(15) are unchanged.
RPARM(16) has the following meaning, where:
If you are doing a factor and solve or a factor only, and:

If RPARM(16) = 0.0, your factorization did not complete successfully, resulting in computational error 2126.
If |RPARM(16)| > 0.0, it is the ratio for row k, a_kk/u_kk, having the maximum absolute value. Row k is indicated in IPARM(16), and:

If IPARM(3) = 0, the ratio corresponds to one of the rows, 1 through n, in the full factorization.
If IPARM(3) > 0, the ratio corresponds to one of the rows, IPARM(3)+1 through n, in the partial factorization.

If you are doing a solve only, this argument is not used in the computation and is unchanged.
RPARM(17) and RPARM(18) have the following meaning, where:
If you are computing the determinant of matrix A, then RPARM(17) is the mantissa, detbas, and RPARM(18) is the power of 10, detpwr, used to express the value of the determinant: detbas(10^detpwr), where 1 <= detbas < 10. Also:

If IPARM(3) = 0, the determinant is computed for columns 1 through n in the full factorization.
If IPARM(3) > 0, the determinant is computed for columns IPARM(3)+1 through n in the partial factorization.

If you are not computing the determinant of matrix A, these arguments are not used in the computation and are unchanged.
RPARM(19) through RPARM(25) are reserved.

Returned as: a one-dimensional array of (at least) length 25, containing long-precision real numbers.

bx

has the following meaning, where:

If you are doing a factor and solve or a solve only, bx is the array, containing the mbx solution vectors x of the system Ax = b or A^Tx = b. Each vector x is length n and is stored in the corresponding column of the array. (If mbx = 0, then bx is unchanged on output.)

If you are doing a factor only, this argument is not used in the computation and is unchanged.

Returned as: an ldbx by (at least) mbx array, containing long-precision real numbers.

Notes

If you set either IPARM(1) = 0 or IPARM(10) = 0, indicating you want to use the default values for IPARM(11) through IPARM(15) and RPARM(10), then:
- Matrix A must be positive definite.
- No pivots are fixed, using RPARM(11) through RPARM(15) values.
- No small pivots are tolerated; that is, the value should be |pivot| > RPARM(10).
Many of the input and output parameters for iparm and rparm are defined for the five pivot regions handled by this subroutine. The limits of the regions are based on RPARM(10), as shown in Figure 11. The pivot values in each region are:

Region 1: pivot < -RPARM(10)
Region 2: -RPARM(10) <= pivot < 0
Region 3: pivot = 0
Region 4: 0 < pivot <= RPARM(10)
Region 5: pivot > RPARM(10)

Figure 11. Five Pivot Regions
The IPARM(4) and IPARM(5) arguments allow you to specify the same or different skyline storage modes for your input and output arrays for matrix A. This allows you to change storage modes as needed. However, if you are concerned with performance, you should use diagonal-out skyline storage mode for both input and output, if possible, because there is less overhead.
For a description of how sparse matrices are stored in skyline storage mode, see Profile-In Skyline Storage Mode and Diagonal-Out Skyline Storage Mode.
Following is an illustration of the portion of matrix A factored in the partial factorization when IPARM(3) > 0. In this case, the subroutine assumes that rows and columns 1 through IPARM(3) are already factored and that rows and columns IPARM(3)+1 through n are to be factored in this computation.

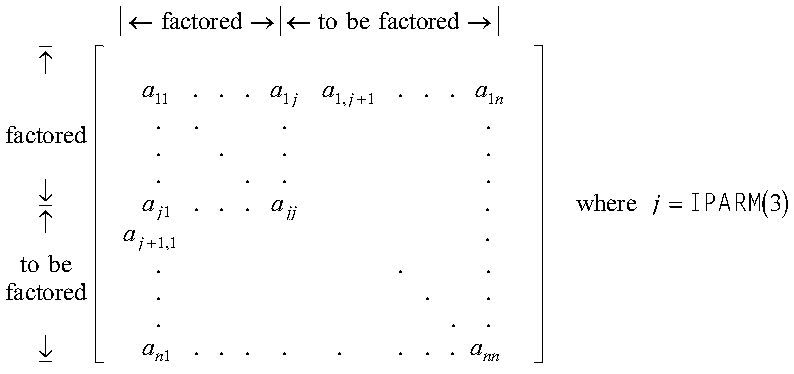
You use the partial factorization function when, for design or storage reasons, you must factor the matrix A in stages. When doing a partial factorization, you must use the same skyline storage mode for all parts of the matrix as it is progressively factored.
Your various arrays must have no common elements; otherwise, results are unpredictable.
You have the option of having the minimum required value for naux dynamically returned to your program. For details, see Using Auxiliary Storage in ESSL.

Function

This subroutine can factor, compute the determinant of, and solve general sparse matrix A, stored in skyline storage mode. For all computations, input matrix A can be stored in either diagonal-out or profile-in skyline storage mode. Output matrix A can also be stored in either of these modes and can be different from the mode used for input.

Matrix A is factored into the following form using specified pivot processing:

A = LU

where:

U is an upper triangular matrix.

L is a lower triangular matrix.

The transformed matrix A, factored into its LU form, is stored in packed format in arrays AU and AL. The inverse of the diagonal of matrix U is stored in the corresponding elements of array AU. The off-diagonal elements of the upper triangular matrix U are stored in the corresponding off-diagonal elements of array AU. The off-diagonal elements of the lower triangular matrix L are stored in the corresponding off-diagonal elements of array AL. (The diagonal elements stored in array AL do not have meaningful values.)

The partial factorization of matrix A, which you can do when you specify the factor-only option, assumes that the first IPARM(3) rows and columns are already factored in the input matrix. It factors the remaining n-IPARM(3) rows and columns in matrix A. (See Notes for an illustration.) It updates only the elements in arrays AU and AL corresponding to the part of matrix A that is factored.

The determinant can be computed with any of the factorization computations. With a full factorization, you get the determinant for the whole matrix. With a partial factorization, you get the determinant for only that part of the matrix factored in this computation.

The system Ax = b or A^Tx = b, having multiple right-hand sides, is solved for x, using the transformed matrix A produced by this call or a subsequent call to this subroutine.

See references [9], [12], [25], [47], and [71]. If n is 0, no computation is performed. If mbx is 0, no solve is performed.

Error Conditions

Resource Errors

Error 2015 is unrecoverable, naux = 0, and unable to allocate work area.
Unable to allocate internal work area.

Computational Errors

If a pivot occurs in region i for i = 1,5 and IPARM(10+i) = 1, the pivot value is replaced with RPARM(10+i), an attention message is issued, and processing continues.
Unacceptable pivot values occurred in the factorization of matrix A.
- One or more diagonal elements of U contains unacceptable pivots and no valid fixup is applicable. The row number i of the first unacceptable pivot element is identified in the computational error message.
- The return code is set to 2.
- i can be determined at run time by use of the ESSL error-handling facilities. To obtain this information, you must use ERRSET to change the number of allowable errors for error code 2126 in the ESSL error option table; otherwise, the default value causes your program to terminate when this error occurs. For details, see What Can You Do about ESSL Computational Errors?.

Input-Argument Errors

n < 0
nu < 0
IDU(n+1) > nu+1
IDU(i+1) <= IDU(i) for i = 1, n
IDU(i+1) > IDU(i)+i and IPARM(4) = 0 for i = 1, n
IDU(i) > IDU(i-1)+i and IPARM(4) = 1 for i = 2, n
nl < 0
IDL(n+1) > nl+1
IDL(i+1) <= IDL(i) for i = 1, n
IDL(i+1) > IDL(i)+i and IPARM(4) = 0 for i = 1, n
IDL(i) > IDL(i-1)+i and IPARM(4) = 1 for i = 2, n
IPARM(1) <> 0 or 1
IPARM(2) <> 0, 1, 2, 10, 11, 100, 102, or 110
IPARM(3) < 0
IPARM(3) > n
IPARM(3) > 0 and IPARM(2) <> 1 or 11
IPARM(4), IPARM(5) <> 0 or 1
IPARM(2) = 0, 1, 10, 11, 100, or 110 and:

IPARM(10) <> 0 or 1
IPARM(11), IPARM(12) <> -1, 0, or 1
IPARM(13) <> -1 or 1
IPARM(14), IPARM(15) <> -1, 0, or 1
RPARM(10) < 0.0
RPARM(10+i) = 0.0 and IPARM(10+i) = 1 for i = 1,5
IPARM(2) = 0, 2, 10, 100, 102, or 110 and:

ldbx <= 0 and mbx <> 0 and n <> 0
ldbx < 0 and mbx = 0
ldbx < n and mbx <> 0
mbx < 0
Error 2015 is recoverable or naux<>0, and naux is too small--that is, less than the minimum required value. Return code 1 is returned if error 2015 is recoverable.

Example 1

This example shows how to factor a 9 by 9 general sparse matrix A and solve the system Ax = b with three right-hand sides. The default values are used for IPARM and RPARM. Input matrix A, shown here, is stored in diagonal-out skyline storage mode. Matrix A is:

        *                                               *
        | 2.0  2.0  2.0  0.0  0.0  0.0   0.0  0.0   0.0 |
        | 2.0  4.0  4.0  2.0  2.0  0.0   0.0  0.0   2.0 |
        | 2.0  4.0  6.0  4.0  4.0  0.0   2.0  0.0   4.0 |
        | 2.0  4.0  6.0  6.0  6.0  2.0   4.0  0.0   6.0 |
        | 0.0  0.0  0.0  2.0  4.0  4.0   4.0  2.0   4.0 |
        | 0.0  2.0  4.0  6.0  8.0  6.0   8.0  4.0  10.0 |
        | 0.0  0.0  0.0  2.0  4.0  6.0   8.0  6.0   8.0 |
        | 0.0  0.0  0.0  2.0  4.0  6.0   8.0  8.0  10.0 |
        | 2.0  4.0  6.0  6.0  8.0  6.0  10.0  8.0  16.0 |
        *                                               *

Output matrix A, shown here, is in LU factored form with U^-1 on the diagonal, and is stored in diagonal-out skyline storage mode. Matrix B is:

        *                                             *
        | 0.5  2.0  2.0  0.0  0.0  0.0  0.0  0.0  0.0 |
        | 1.0  0.5  2.0  2.0  2.0  0.0  0.0  0.0  2.0 |
        | 1.0  1.0  0.5  2.0  2.0  0.0  2.0  0.0  2.0 |
        | 1.0  1.0  1.0  0.5  2.0  2.0  2.0  0.0  2.0 |
        | 0.0  0.0  0.0  1.0  0.5  2.0  2.0  2.0  2.0 |
        | 0.0  1.0  1.0  1.0  1.0  0.5  2.0  2.0  2.0 |
        | 0.0  0.0  0.0  1.0  1.0  1.0  0.5  2.0  2.0 |
        | 0.0  0.0  0.0  1.0  1.0  1.0  1.0  0.5  2.0 |
        | 1.0  1.0  1.0  1.0  1.0  1.0  1.0  1.0  0.5 |
        *                                             *

Call Statement and Input

            N   AU  NU  IDU  AL  NL  IDL  IPARM  RPARM  AUX  NAUX  BX  LDBX MBX
            |   |   |    |   |   |    |     |      |     |    |    |    |    |
CALL DGKFS( 9 , AU, 33, IDU, AL, 35, IDL, IPARM, RPARM, AUX,  57 , BX , 12 , 3 )

AU       =  (2.0, 4.0, 2.0, 6.0, 4.0, 2.0, 6.0, 4.0, 2.0, 4.0, 6.0,
             4.0, 2.0, 6.0, 4.0, 2.0, 8.0, 8.0, 4.0, 4.0, 2.0, 8.0,
             6.0, 4.0, 2.0, 16.0, 10.0, 8.0, 10.0, 4.0, 6.0, 4.0, 2.0)
IDU      =  (1, 2, 4, 7, 10, 14, 17, 22, 26, 34)
AL       =  (0.0, 0.0, 2.0, 0.0, 4.0, 2.0, 0.0, 6.0, 4.0, 2.0, 0.0,
             2.0, 0.0, 8.0, 6.0, 4.0, 2.0, 0.0, 6.0, 4.0, 2.0, 0.0,
             8.0, 6.0, 4.0, 2.0, 0.0, 8.0, 10.0, 6.0, 8.0, 6.0, 6.0,
             4.0, 2.0)
IDL      =  (1, 2, 4, 7, 11, 13, 18, 22, 27, 36)
IPARM    =  (0, . , . , . , . , . , . , . , . , . , . , . , . , . ,
             . , . , . , . , . , . , . , . , . , . , . )

RPARM =(not relevant)

        *                       *
        |  6.00   12.00   18.00 |
        | 16.00   32.00   48.00 |
        | 26.00   52.00   78.00 |
        | 36.00   72.00  108.00 |
        | 20.00   40.00   60.00 |
BX   =  | 48.00   96.00  144.00 |
        | 34.00   68.00  102.00 |
        | 38.00   76.00  114.00 |
        | 66.00  132.00  198.00 |
        |   .       .       .   |
        |   .       .       .   |
        |   .       .       .   |
        *                       *

Output

AU = (0.5, 0.5, 2.0, 0.5, 2.0, 2.0, 0.5, 2.0, 2.0, 0.5, 2.0,
2.0, 2.0, 0.5, 2.0, 2.0, 0.5, 2.0, 2.0, 2.0, 2.0, 0.5,
2.0, 2.0, 2.0, 0.5, 2.0, 2.0, 2.0, 2.0, 2.0, 2.0, 2.0)
IDU =(same as input)
AL = (0.0, 0.0, 1.0, 0.0, 1.0, 1.0, 0.0, 1.0, 1.0, 1.0, 0.0,
1.0, 0.0, 1.0, 1.0, 1.0, 1.0, 0.0, 1.0, 1.0, 1.0, 0.0,
1.0, 1.0, 1.0, 1.0, 0.0, 1.0, 1.0, 1.0, 1.0, 1.0, 1.0,
1.0, 1.0)
IDL =(same as input)
IPARM = (0, . , . , . , . , . , . , . , . , . , . , . , . , . ,
. , 9, . , . , . , . , 0, 0, 0, 0, 9)
RPARM = ( . , . , . , . , . , . , . , . , . , . , . , . , . , . ,
. , 8.0, . , . , . , . , . , . , . , . , . )

        *                  *
        | 1.00  2.00  3.00 |
        | 1.00  2.00  3.00 |
        | 1.00  2.00  3.00 |
        | 1.00  2.00  3.00 |
        | 1.00  2.00  3.00 |
BX   =  | 1.00  2.00  3.00 |
        | 1.00  2.00  3.00 |
        | 1.00  2.00  3.00 |
        | 1.00  2.00  3.00 |
        |  .     .     .   |
        |  .     .     .   |
        |  .     .     .   |
        *                  *

Example 2

This example shows how to factor the 9 by 9 general sparse matrix A from Example 1, solve the system A^Tx = b with three right-hand sides, and compute the determinant of A. The default values for pivot processing are used for IPARM. Input matrix A is stored in profile-in skyline storage mode. Output matrix A is in LU factored form with U^-1 on the diagonal, and is stored in diagonal-out skyline storage mode. It is the same as output matrix A in Example 1.

Call Statement and Input

            N  AU  NU  IDU  AL  NL  IDL  IPARM  RPARM  AUX  NAUX  BX  LDBX MBX
            |  |   |    |   |   |    |     |       |     |   |    |     |   |
CALL DGKFS( 9, AU, 33, IDU, AL, 35, IDL, IPARM, RPARM, AUX,  57 , BX , 12 , 3 )

AU       =  (2.0, 2.0, 4.0, 2.0, 4.0, 6.0, 2.0, 4.0, 6.0, 2.0, 4.0,
             6.0, 4.0, 2.0, 4.0, 6.0, 2.0, 4.0, 4.0, 8.0, 8.0, 2.0,
             4.0, 6.0, 8.0, 2.0, 4.0, 6.0, 4.0, 10.0, 8.0, 10.0, 16.0)
IDU      =  (1, 3, 6, 9, 13, 16, 21, 25, 33, 34)
AL       =  (0.0, 2.0, 0.0, 2.0, 4.0, 0.0, 2.0, 4.0, 6.0, 0.0, 2.0,
             0.0, 2.0, 4.0, 6.0, 8.0, 0.0, 2.0, 4.0, 6.0, 0.0, 2.0,
             4.0, 6.0, 8.0, 0.0, 2.0, 4.0, 6.0, 6.0, 8.0, 6.0, 10.0,
             8.0, 0.0)
IDL      =  (1, 3, 6, 10, 12, 17, 21, 26, 35, 36)
IPARM    =  (1, 110, 0, 1, 0, . , . , . , . , 0, . , . , . , . , . ,
             . , . , . , . , . , . , . , . , . , . )

RPARM =(not relevant)

        *                       *
        | 10.00   20.00   30.00 |
        | 20.00   40.00   60.00 |
        | 28.00   56.00   84.00 |
        | 30.00   60.00   90.00 |
        | 40.00   80.00  120.00 |
BX   =  | 30.00   60.00   90.00 |
        | 44.00   88.00  132.00 |
        | 28.00   56.00   84.00 |
        | 60.00  120.00  180.00 |
        |   .       .       .   |
        |   .       .       .   |
        |   .       .       .   |
        *                       *

Output

AU =(same as output AU in Example 1)
IDU =(same as output IDU in Example 1)
AL =(same as output AL in Example 1)
IDL =(same as output IDL in Example 1)
IPARM = (1, 110, 0, 1, 0, . , . , . , . , 0, . , . , . , . , . ,
9, . , . , . , . , 0, 0, 0, 0, 9)
RPARM = ( . , . , . , . , . , . , . , . , . , . , . , . , . , . ,
. , 8.0, 5.12, 2.0, . , . , . , . , . , . , . )
BX =(same as output BX in Example 1)

Example 3

This example shows how to factor a 9 by 9 negative-definite general sparse matrix A, solve the system Ax = b with three right-hand sides, and compute the determinant of A. (Default values for pivot processing are not used for IPARM because A is negative-definite.) Input matrix A, shown here, is stored in diagonal-out skyline storage mode:

        *                                                        *
        | -2.0  -2.0  -2.0   0.0   0.0   0.0    0.0   0.0    0.0 |
        | -2.0  -4.0  -4.0  -2.0  -2.0   0.0    0.0   0.0   -2.0 |
        | -2.0  -4.0  -6.0  -4.0  -4.0   0.0   -2.0   0.0   -4.0 |
        | -2.0  -4.0  -6.0  -6.0  -6.0  -2.0   -4.0   0.0   -6.0 |
        |  0.0   0.0   0.0  -2.0  -4.0  -4.0   -4.0  -2.0   -4.0 |
        |  0.0  -2.0  -4.0  -6.0  -8.0  -6.0   -8.0  -4.0  -10.0 |
        |  0.0   0.0   0.0  -2.0  -4.0  -6.0   -8.0  -6.0   -8.0 |
        |  0.0   0.0   0.0  -2.0  -4.0  -6.0   -8.0  -8.0  -10.0 |
        | -2.0  -4.0  -6.0  -6.0  -8.0  -6.0  -10.0  -8.0  -16.0 |
        *                                                        *

Output matrix A, shown here, is in LU factored form with U^-1 on the diagonal, and is stored in diagonal-out skyline storage mode. Matrix A is:

         *                                                      *
         | -0.5  -2.0  -2.0   0.0   0.0   0.0   0.0   0.0   0.0 |
         |  1.0  -0.5  -2.0  -2.0  -2.0   0.0   0.0   0.0  -2.0 |
         |  1.0   1.0  -0.5  -2.0  -2.0   0.0  -2.0   0.0  -2.0 |
         |  1.0   1.0   1.0  -0.5  -2.0  -2.0  -2.0   0.0  -2.0 |
         |  0.0   0.0   0.0   1.0  -0.5  -2.0  -2.0  -2.0  -2.0 |
         |  0.0   1.0   1.0   1.0   1.0  -0.5  -2.0  -2.0  -2.0 |
         |  0.0   0.0   0.0   1.0   1.0   1.0  -0.5  -2.0  -2.0 |
         |  0.0   0.0   0.0   1.0   1.0   1.0   1.0  -0.5  -2.0 |
         |  1.0   1.0   1.0   1.0   1.0   1.0   1.0   1.0  -0.5 |
         *                                                      *

Call Statement and Input

            N  AU  NU  IDU  AL  NL  IDL  IPARM  RPARM  AUX  NAUX  BX  LDBX MBX
            |  |   |    |   |   |    |     |      |     |    |    |    |    |
CALL DGKFS( 9, AU, 33, IDU, AL, 35, IDL, IPARM, RPARM, AUX,  57 , BX , 12 , 3 )

AU       =  (-2.0, -4.0, -2.0, -6.0, -4.0, -2.0, -6.0, -4.0, -2.0,
             -4.0, -6.0, -4.0, -2.0, -6.0, -4.0, -2.0, -8.0, -8.0,
             -4.0, -4.0, -2.0, -8.0, -6.0, -4.0, -2.0, -16.0, -10.0,
             -8.0, -10.0, -4.0, -6.0, -4.0, -2.0)
IDU      =  (1, 2, 4, 7, 10, 14, 17, 22, 26, 34)
AL       =  (0.0, 0.0, -2.0, 0.0, -4.0, -2.0, 0.0, -6.0, -4.0, -2.0,
             0.0, -2.0, 0.0, -8.0, -6.0, -4.0, -2.0, 0.0, -6.0, -4.0,
             -2.0, 0.0, -8.0, -6.0, -4.0, -2.0, 0.0, -8.0, -10.0,
             -6.0, -8.0, -6.0, -6.0, -4.0, -2.0)
IDL      =  (1, 2, 4, 7, 11, 13, 18, 22, 27, 36)
IPARM    =  (1, 10, 0, 0, 0, . , . , . , . , 1, 0, -1, -1, -1, -1, . ,
             . , . , . , . , . , . , . , . , . )

RPARM = ( . , . , . , . , . , . , . , . , . , 10^-15, . , . ,
. , . , . , . , . , . , . , . , . , . , . , . , . )
BX =(same as input BX in Example 1)

Output

AU = (-0.5, -0.5, -2.0, -0.5, -2.0, -2.0, -0.5, -2.0, -2.0,
-0.5, -2.0, -2.0, -2.0, -0.5, -2.0, -2.0, -0.5, -2.0,
-2.0, -2.0, -2.0, -0.5, -2.0, -2.0, -2.0, -0.5, -2.0,
-2.0, -2.0, -2.0, -2.0, -2.0, -2.0)
IDU =(same as input)
AL = (0.0, 0.0, 1.0, 0.0, 1.0, 1.0, 0.0, 1.0, 1.0, 1.0, 0.0,
1.0, 0.0, 1.0, 1.0, 1.0, 1.0, 0.0, 1.0, 1.0, 1.0, 0.0,
1.0, 1.0, 1.0, 1.0, 0.0, 1.0, 1.0, 1.0, 1.0, 1.0, 1.0,
1.0, 1.0)
IDL =(same as input)
IPARM = (1, 10, 0, 0, 0, . , . , . , . , 1, 0, -1, -1, -1, -1, 9,
. , . , . , . , 9, 0, 0, 0, 0)
RPARM = ( . , . , . , . , . , . , . , . , . , 10^-15, . , . ,
. , . , . , 8.0, -5.12, 2.0, . , . , . , . , . , . , . )

        *                     *
        | -1.00  -2.00  -3.00 |
        | -1.00  -2.00  -3.00 |
        | -1.00  -2.00  -3.00 |
        | -1.00  -2.00  -3.00 |
        | -1.00  -2.00  -3.00 |
BX   =  | -1.00  -2.00  -3.00 |
        | -1.00  -2.00  -3.00 |
        | -1.00  -2.00  -3.00 |
        | -1.00  -2.00  -3.00 |
        |   .      .      .   |
        |   .      .      .   |
        |   .      .      .   |
        *                     *

Example 4

This example shows how to factor the first six rows and columns, referred to as matrix A1, of the 9 by 9 general sparse matrix A from Example 1 and compute the determinant of A1. Input matrix A1, shown here, is stored in diagonal-out skyline storage mode. Input matrix A1 is:

                     *                              *
                     | 2.0  2.0  2.0  0.0  0.0  0.0 |
                     | 2.0  4.0  4.0  2.0  2.0  0.0 |
                     | 2.0  4.0  6.0  4.0  4.0  0.0 |
                     | 2.0  4.0  6.0  6.0  6.0  2.0 |
                     | 0.0  0.0  0.0  2.0  4.0  4.0 |
                     | 0.0  2.0  4.0  6.0  8.0  6.0 |
                     *                              *

Output matrix A1, shown here, is in LU factored form with U^-1 on the diagonal, and is stored in diagonal-out skyline storage mode. Output matrix A1 is:

                     *                              *
                     | 0.5  2.0  2.0  0.0  0.0  0.0 |
                     | 1.0  0.5  2.0  2.0  2.0  0.0 |
                     | 1.0  1.0  0.5  2.0  2.0  0.0 |
                     | 1.0  1.0  1.0  0.5  2.0  2.0 |
                     | 0.0  0.0  0.0  1.0  0.5  2.0 |
                     | 0.0  1.0  1.0  1.0  1.0  0.5 |
                     *                              *

Call Statement and Input

            N  AU  NU  IDU  AL  NL  IDL  IPARM  RPARM  AUX  NAUX  BX   LDBX   MBX
            |  |   |    |   |   |    |     |      |     |    |    |     |      |
CALL DGKFS( 6, AU, 33, IDU, AL, 35, IDL, IPARM, RPARM, AUX,  45 , BX , LDBX , MBX )

AU =(same as input AU in Example 1)
IDU = (1, 2, 4, 7, 10, 14, 17)
AL =(same as input AL in Example 1)
IDL = (1, 2, 4, 7, 11, 13, 18)
IPARM = (1, 11, 0, 0, 0, . , . , . , . , 0, . , . , . , . , . ,
. , . , . , . , . , . , . , . , . , . )
RPARM =(not relevant)
BX =(not relevant)
LDBX =(not relevant)
MBX =(not relevant)

Output

AU = (0.5, 0.5, 2.0, 0.5, 2.0, 2.0, 0.5, 2.0, 2.0, 0.5, 2.0,
2.0, 2.0, 0.5, 2.0, 2.0, 8.0, 8.0, 4.0, 4.0, 2.0, 8.0,
6.0, 4.0, 2.0, 16.0, 10.0, 8.0, 10.0, 4.0, 6.0, 4.0, 2.0)
IDU =(same as input)
AL = (0.0, 0.0, 1.0, 0.0, 1.0, 1.0, 0.0, 1.0, 1.0, 1.0, 0.0,
1.0, 0.0, 1.0, 1.0, 1.0, 1.0, 0.0, 6.0, 4.0, 2.0, 0.0,
8.0, 6.0, 4.0, 2.0, 0.0, 8.0, 10.0, 6.0, 8.0, 6.0, 6.0,
4.0, 2.0)
IDL =(same as input)
IPARM = (1, 11, 0, 0, 0, . , . , . , . , 0, . , . , . , . , . , 3,
. , . , . , . , 0, 0, 0, 0, 6)
RPARM = ( . , . , . , . , . , . , . , . , . , . , . , . , . , . ,
. , 3.0, 6.4, 1.0, . , . , . , . , . , . , . )
BX =(same as input)
LDBX =(same as input)
MBX =(same as input)

Example 5

This example shows how to do a partial factorization of the 9 by 9 general sparse matrix A from Example 1, where the first six rows and columns were factored in Example 4. It factors the remaining three rows and columns and computes the determinant of that part of the matrix. The input matrix, referred to as A2, shown here, is made up of the output factored matrix A1 plus the three remaining unfactored rows and columns of matrix A. Matrix A2 is:

            *                                               *
            | 0.5  2.0  2.0  0.0  0.0  0.0   0.0  0.0   0.0 |
            | 1.0  0.5  2.0  2.0  2.0  0.0   0.0  0.0   2.0 |
            | 1.0  1.0  0.5  2.0  2.0  0.0   2.0  0.0   4.0 |
            | 1.0  1.0  1.0  0.5  2.0  2.0   4.0  0.0   6.0 |
            | 0.0  0.0  0.0  1.0  0.5  2.0   4.0  2.0   4.0 |
            | 0.0  1.0  1.0  1.0  1.0  0.5   8.0  4.0  10.0 |
            | 0.0  0.0  0.0  2.0  4.0  6.0   8.0  6.0   8.0 |
            | 0.0  0.0  0.0  2.0  4.0  6.0   8.0  8.0  10.0 |
            | 2.0  4.0  6.0  6.0  8.0  6.0  10.0  8.0  16.0 |
            *                                               *

Both parts of input matrix A2 are stored in diagonal-out skyline storage mode.

Output matrix A2 is the same as output matrix A in Example 1 and is stored in diagonal-out skyline storage mode.

Call Statement and Input

            N  AU  NU  IDU  AL  NL  IDL  IPARM  RPARM  AUX  NAUX  BX   LDBX   MBX
            |  |   |    |   |   |    |     |      |     |    |    |     |      |
CALL DGKFS( 9, AU, 33, IDU, AL, 35, IDL, IPARM, RPARM, AUX,  45 , BX , LDBX , MBX )

AU =(same as output AU in Example 4)
IDU =(same as input IDU in Example 1)
AL =(same as output AL in Example 4)
IDL =(same as input IDL in Example 1)
IPARM = (1, 11, 6, 0, 0, . , . , . , . , 0, . , . , . , . , . ,
. , . , . , . , . , . , . , . , . , . )
RPARM =(not relevant)
BX =(not relevant)
LDBX =(not relevant)
MBX =(not relevant)

Output

AU =(same as output AU in Example 1)
IDU =(same as output IDU in Example 1)
AL =(same as output AL in Example 1)
IDL =(same as output IDL in Example 1)
IPARM = (1, 11, 6, 0, 0, . , . , . , . , 0, . , . , . , . , . , 9,
. , . , . , . , 0, 0, 0, 0, 3)
RPARM = ( . , . , . , . , . , . , . , . , . , . , . , . , . , . ,
. , 8.0, 8.0, 0.0, . , . , . , . , . , . , . )
BX =(same as input)
LDBX =(same as input)
MBX =(same as input)

Example 6

This example shows how to solve the system Ax = b with one right-hand side for a general sparse matrix A. Input matrix A, used here, is the same as factored output matrix A from Example 1, stored in profile-in skyline storage mode. Here, output matrix A is unchanged on output and is stored in profile-in skyline storage mode.

Call Statement and Input

            N  AU  NU  IDU  AL  NL  IDL  IPARM  RPARM  AUX NAUX  BX  LDBX MBX
            |  |   |    |   |   |    |     |      |     |   |    |    |    |
CALL DGKFS( 9, AU, 33, IDU, AL, 35, IDL, IPARM, RPARM, AUX, 49 , BX , 9 ,  1 )

AU = (0.5, 2.0, 0.5, 2.0, 2.0, 0.5, 2.0, 2.0, 0.5, 2.0, 2.0,
2.0, 0.5, 2.0, 2.0, 0.5, 2.0, 2.0, 2.0, 2.0, 0.5, 2.0,
2.0, 2.0, 0.5, 2.0, 2.0, 2.0, 2.0, 2.0, 2.0, 2.0, 0.5)
IDU = (1, 3, 6, 9, 13, 16, 21, 25, 33, 34)
AL = (0.0, 1.0, 0.0, 1.0, 1.0, 0.0, 1.0, 1.0, 1.0, 0.0, 1.0,
0.0, 1.0, 1.0, 1.0, 1.0, 0.0, 1.0, 1.0, 1.0, 0.0, 1.0,
1.0, 1.0, 1.0, 0.0, 1.0, 1.0, 1.0, 1.0, 1.0, 1.0, 1.0,
1.0, 0.0)
IDL = (1, 3, 6, 10, 12, 17, 21, 26, 35, 36)
IPARM = (1, 2, 0, 1, 1, . , . , . , . , . , . , . , . , . , . ,
. , . , . , . , . , . , . , . , . , . )
RPARM =(not relevant)
BX = (12.0, 58.0, 114.0, 176.0, 132.0, 294.0, 240.0, 274.0,
406.0)

Output

AU =(same as input)
IDU =(same as input)
AL =(same as input)
IDL =(same as input)
IPARM =(same as input)
RPARM =(not relevant)
BX = (1.0, 2.0, 3.0, 4.0, 5.0, 6.0, 7.0, 8.0, 9.0)

[ Top of Page | Previous Page | Next Page | Table of Contents | Index ]