Engineering and Scientific Subroutine Library for AIX Version 3 Release 3: Guide and Reference

SGESVF and DGESVF--Singular Value Decomposition for a General Matrix

These subroutines compute the singular value decomposition of general matrix A in preparation for solving linear least squares problems. To compute the minimal norm linear least squares solution of AX is congruent to B, follow the call to these subroutines with a call to SGESVS or DGESVS, respectively.

Table 117. Data Types

A, B, s, `aux`	Subroutine
Short-precision real	SGESVF
Long-precision real	DGESVF

Syntax

Fortran	CALL SGESVF \| DGESVF (`iopt`, `a`, `lda`, `b`, `ldb`, `nb`, `s`, `m`, `n`, `aux`, `naux`)
C and C++	sgesvf \| dgesvf (`iopt`, `a`, `lda`, `b`, `ldb`, `nb`, `s`, `m`, `n`, `aux`, `naux`);
PL/I	CALL SGESVF \| DGESVF (`iopt`, `a`, `lda`, `b`, `ldb`, `nb`, `s`, `m`, `n`, `aux`, `naux`);

On Entry

iopt

indicates the type of computation to be performed, where:

If iopt = 0 or 10, singular values are computed.

If iopt = 1 or 11, singular values and V are computed.

If iopt = 2 or 12, singular values, V, and U^TB are computed.

Specified as: a fullword integer; iopt = 0, 1, 2, 10, 11, or 12.

If iopt < 10, singular values are unordered.

If iopt >= 10, singular values are sorted in descending order and, if applicable, the columns of V and the rows of U^TB are swapped to correspond to the sorted singular values.

a

is the m by n general matrix A, whose singular value decomposition is to be computed. Specified as: an lda by (at least) n array, containing numbers of the data type indicated in Table 117.

lda

is the leading dimension of the array specified for a. Specified as: a fullword integer; lda > 0 and lda >= max(m, n).

b

has the following meaning, where:

If iopt = 0, 1, 10, or 11, this argument is not used in the computation.

If iopt = 2 or 12, it is the m by nb matrix B.

Specified as: an ldb by (at least) nb array, containing numbers of the data type indicated in Table 117.

If this subroutine is followed by a call to SGESVS or DGESVS, B should contain the right-hand side of the linear least squares problem, AX is congruent to B. (The nb column vectors of B contain right-hand sides for nb distinct linear least squares problems.) However, if the matrix U^T is desired on output, B should be equal to the identity matrix of order m.

ldb

has the following meaning, where:

If iopt = 0, 1, 10, or 11, this argument is not used in the computation.

If iopt = 2 or 12, it is the leading dimension of the array specified for b.

Specified as: a fullword integer. It must have the following values, where:

If iopt = 0, 1, 10, or 11, ldb > 0.

If iopt = 2 or 12, ldb > 0 and ldb >= max(m, n).

nb

has the following meaning, where:

If iopt = 0, 1, 10, or 11, this argument is not used in the computation.

If iopt = 2 or 12, it is the number of columns in matrix B.

Specified as: a fullword integer; if iopt = 2 or 12, nb > 0.

s

See On Return.

m

is the number of rows in matrices A and B. Specified as: a fullword integer; m >= 0.

n

is the number of columns in matrix A and the number of elements in vector s. Specified as: a fullword integer; n >= 0.

aux

has the following meaning:

If naux = 0 and error 2015 is unrecoverable, aux is ignored.

Otherwise, it is the storage work area used by this subroutine. Its size is specified by naux.

Specified as: an area of storage, containing numbers of the data type indicated in Table 117.

naux

is the size of the work area specified by aux--that is, the number of elements in aux. Specified as: a fullword integer, where:

If naux = 0 and error 2015 is unrecoverable, SGESVF and DGESVF dynamically allocate the work area used by the subroutine. The work area is deallocated before control is returned to the calling program.

Otherwise, It must have the following value, where:

If iopt = 0 or 10, naux >= n+max(m, n).

If iopt = 1 or 11, naux >= 2n+max(m, n).

If iopt = 2 or 12, naux >= 2n+max(m, n, nb).

On Return

a

has the following meaning, where:

If iopt = 0, or 10, A is overwritten; that is, the original input is not preserved.

If iopt = 1, 2, 11, or 12, A contains the real orthogonal matrix V, of order n, in its first n rows and n columns. If iopt = 11 or 12, the columns of V are swapped to correspond to the sorted singular values. If m > n, rows n+1, n+2, ..., m of array A are overwritten; that is, the original input is not preserved.

Returned as: an lda by (at least) n array, containing numbers of the data type indicated in Table 117.

b

has the following meaning, where:

If iopt = 0, 1, 10, or 11, B is not used in the computation.

If iopt = 2 or 12, B is overwritten by the n by nb matrix U^TB.

If iopt = 12, the rows of U^TB are swapped to correspond to the sorted singular values. If m > n, rows n+1, n+2, ..., m of array B are overwritten; that is, the original input is not preserved.

Returned as: an ldb by (at least) nb array, containing numbers of the data type indicated in Table 117.

s

is a the vector s of length n, containing the singular values of matrix A. Returned as: a one-dimensional array of (at least) length n, containing numbers of the data type indicated in Table 117; s_i >= 0, where:

If iopt < 10, the singular values are unordered in s.

If iopt >= 10, the singular values are sorted in descending order in s; that is, s₁ >= s₂ >= ... >= s_n >= 0. If applicable, the columns of V and the rows of U^TB are swapped to correspond to the sorted singular values.

Notes

The following items must have no common elements; otherwise, results are unpredictable: matrices A and B, vector s, and the data area specified for aux.
When you specify iopt = 0, 1, 10, or 11, you must also specify:
- A dummy argument for b
- A positive value for ldb
See Example.
You have the option of having the minimum required value for naux dynamically returned to your program. For details, see Using Auxiliary Storage in ESSL.

Function

The singular value decomposition of a real general matrix is computed as follows:

A = USigmaV^T

where:

U^TU = V^TV = VV^T = I

A is an m by n real general matrix.

V is a real general orthogonal matrix of order n. On output, V overwrites the first n rows and n columns of A.

U^TB is an n by nb real general matrix. On output, U^TB overwrites the first n rows and nb columns of B.

Sigma is an n by n real diagonal matrix. The diagonal elements of Sigma are the singular values of A, returned in the vector s.

If m or n is equal to 0, no computation is performed.

One of the following algorithms is used:

Golub-Reinsch Algorithm (See pages 134 to 151 in reference [99].)
1. Reduce the real general matrix A to bidiagonal form using Householder transformations.
2. Iteratively reduce the bidiagonal form to diagonal form using a variant of the QR algorithm.
Chan Algorithm (See reference [13].)
1. Compute the QR decomposition of matrix A using Householder transformations; that is, A = QR.
2. Apply the Golub-Reinsch Algorithm to the matrix R.
  If R = XWY^T is the singular value decomposition of R, the singular value decomposition of matrix A is given by:
  
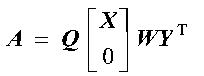
  where:

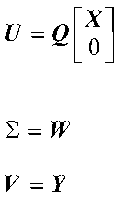
Also, see references [13], [58], [78], and pages 134 to 151 in reference [99]. These algorithms have a tendency to generate underflows that may hurt overall performance. The system default is to mask underflow, which improves the performance of these subroutines.

Error Conditions

Resource Errors

Error 2015 is unrecoverable, naux = 0, and unable to allocate work area.

Computational Errors

Singular value (i) failed to converge after (x) iterations.

The singular values (s_j, j = n, n-1, ..., i+1) are correct. If iopt < 10, they are unordered. Otherwise, they are ordered.
a has been modified.
If iopt = 2 or 12, then b has been modified.
The return code is set to 1.
i and x can be determined at run time by use of the ESSL error-handling facilities. To obtain this information, you must use ERRSET to change the number of allowable errors for error code 2107 in the ESSL error option table; otherwise, the default value causes your program to terminate when this error occurs. See What Can You Do about ESSL Computational Errors?.

Input-Argument Errors

iopt <> 0, 1, 2, 10, 11, or 12
lda <= 0
max(m, n) > lda
ldb <= 0 and iopt = 2, 12
max(m, n) > ldb and iopt = 2, 12
nb <= 0 and iopt = 2, 12
m < 0
n < 0
Error 2015 is recoverable or naux<>0, and naux is too small--that is, less than the minimum required value. Return code 2 is returned if error 2015 is recoverable.

Example 1

This example shows how to find only the singular values, s, of a real long-precision general matrix A, where:

M is greater than N.
NAUX is greater than or equal to N+max(M, N) = 7.
LDB has been set to 1 to avoid a Fortran error message.
DUMMY is a placeholder for argument b, which is not used in the computation.
The singular values are returned in S.
On output, matrix A is overwritten; that is, the original input is not preserved.

Call Statement and Input

            IOPT  A  LDA    B    LDB  NB  S   M   N   AUX  NAUX
             |    |   |     |     |   |   |   |   |    |    |
CALL DGESVF( 0  , A , 4 , DUMMY , 1 , 0 , S , 4 , 3 , AUX , 7  )
 
        *                  *
        |  1.0   2.0   3.0 |
A    =  |  4.0   5.0   6.0 |
        |  7.0   8.0   9.0 |
        | 10.0  11.0  12.0 |
        *                  *

Output

S        =   (25.462, 1.291, 0.000)

Example 2

This example computes the singular values, s, of a real long-precision general matrix A and the matrix V, where:

M is equal to N.
NAUX is greater than or equal to 2N+max(M, N) = 9.
LDB has been set to 1 to avoid a Fortran error message.
DUMMY is a placeholder for argument b, which is not used in the computation.
The singular values are returned in S.
The matrix V is returned in A.

Call Statement and Input

            IOPT  A  LDA    B    LDB  NB  S   M   N   AUX  NAUX
             |    |   |     |     |   |   |   |   |    |    |
CALL DGESVF( 1  , A , 3 , DUMMY , 1 , 0 , S , 3 , 3 , AUX , 9  )
 
        *                *
        |  2.0  1.0  1.0 |
A    =  |  4.0  1.0  0.0 |
        | -2.0  2.0  1.0 |
        *                *

Output

        *                        *
        | -0.994   0.105  -0.041 |
A    =  | -0.112  -0.870   0.480 |
        | -0.015  -0.482  -0.876 |
        *                        *
 
S        =    (4.922, 2.724, 0.597)

Example 3

This example computes the singular values, s, and computes matrices V and U^TB in preparation for solving the underdetermined system AX is congruent to B, where:

M is less than N.
NAUX is greater than or equal to 2N+max(M, N, NB) = 9.
The singular values are returned in S.
The matrix V is returned in A.
The matrix U^TB is returned in B.

Call Statement and Input

            IOPT  A  LDA  B  LDB  NB  S   M   N   AUX  NAUX
             |    |   |   |   |   |   |   |   |    |    |
CALL DGESVF( 2  , A , 3 , B , 3 , 1 , S , 2 , 3 , AUX , 9  )

        *               *
        | 1.0  2.0  2.0 |
A    =  | 2.0  4.0  5.0 |
        |  .    .    .  |
        *               *

        *     *
        | 1.0 |
B    =  | 4.0 |
        |  .  |
        *     *

Output

        *                        *
        | -0.304  -0.894   0.328 |
A    =  | -0.608   0.447   0.656 |
        | -0.733   0.000  -0.680 |
        *                        *
 
        *        *
        | -4.061 |
B    =  |  0.000 |
        | -0.714 |
        *        *
 
S        =   (7.342, 0.000, 0.305)

Example 4

This example computes the singular values, s, and matrices V and U^TB in preparation for solving the overdetermined system AX is congruent to B, where:

M is greater than N.
NAUX is greater than or equal to 2N+max(M, N, NB) = 7.
The singular values are returned in S.
The matrix V is returned in A.
The matrix U^TB is returned in B.

Call Statement and Input

            IOPT  A  LDA  B  LDB  NB  S   M   N   AUX  NAUX
             |    |   |   |   |   |   |   |   |    |    |
CALL DGESVF( 2  , A , 3 , B , 3 , 2 , S , 3 , 2 , AUX , 7  )

        *          *
        | 1.0  4.0 |
A    =  | 2.0  5.0 |
        | 3.0  6.0 |
        *          *

        *           *
        | 7.0  10.0 |
B    =  | 8.0  11.0 |
        | 9.0  12.0 |
        *           *

Output

        *                *
        |  0.922  -0.386 |
A    =  | -0.386  -0.922 |
        |   .       .    |
        *                *

        *                  *
        |  -1.310   -2.321 |
B    =  | -13.867  -18.963 |
        |    .        .    |
        *                  *
 
X        =   (0.773, 9.508)

Example 5

This example computes the singular values, s, and matrices V and U^TB in preparation for solving the overdetermined system AX is congruent to B. The singular values are sorted in descending order, and the columns of V and the rows of U^TB are swapped to correspond to the sorted singular values.

M is greater than N.
NAUX is greater than or equal to 2N+max(M, N, NB) = 7.
The singular values are returned in S.
The matrix V is returned in A.
The matrix U^TB is returned in B.

Call Statement and Input

            IOPT  A  LDA  B  LDB  NB  S   M   N   AUX  NAUX
             |    |   |   |   |   |   |   |   |    |    |
CALL DGESVF( 12 , A , 3 , B , 3 , 2 , S , 3 , 2 , AUX , 7  )

        *          *
        | 1.0  4.0 |
A    =  | 2.0  5.0 |
        | 3.0  6.0 |
        *          *

        *           *
        | 7.0  10.0 |
B    =  | 8.0  11.0 |
        | 9.0  12.0 |
        *           *

Output

        *                *
        | -0.386   0.922 |
A    =  | -0.922  -0.386 |
        |   .       .    |
        *                *

        *                  *
        | -13.867  -18.963 |
B    =  |  -1.310   -2.321 |
        |   .         .    |
        *                  *
 
S        =   (9.508, 0.773)

[ Top of Page | Previous Page | Next Page | Table of Contents | Index ]