Engineering and Scientific Subroutine Library for AIX Version 3 Release 3: Guide and Reference

SCOSF and DCOSF--Cosine Transform

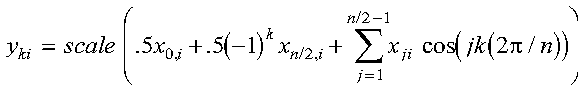
These subroutines compute a set of m real even discrete n-point Fourier transforms of cosine sequences of real even data.

Table 134. Data Types

Note:

Two invocations of this subroutine are necessary: one to prepare the working storage for the subroutine, and the other to perform the computations.

Syntax

On Entry

init

is a flag, where:

If init <> 0, trigonometric functions and other parameters, depending on arguments other than x, are computed and saved in aux1. The contents of x and y are not used or changed.

If init = 0, the discrete Fourier transforms of the given sequences are computed. The only arguments that may change after initialization are x, y, and aux2. All scalar arguments must be the same as when the subroutine was called for initialization with init <> 0.

Specified as: a fullword integer. It can have any value.

x

is the array X, consisting of m sequences of length n/2+1. Specified as: an array of (at least) length 1+(n/2)inc1x+(m-1)inc2x, containing numbers of the data type indicated in Table 134.

inc1x

is the stride between the elements within each sequence in array X. Specified as: a fullword integer; inc1x > 0.

inc2x

is the stride between the first elements of the sequences in array X. (If m = 1, this argument is ignored.) Specified as: a fullword integer; inc2x > 0.

y

See On Return.

inc1y

is the stride between the elements within each sequence in array Y. Specified as: a fullword integer; inc1y > 0.

inc2y

is the stride between the first elements of the sequences in array Y. (If m = 1, this argument is ignored.) Specified as: a fullword integer; inc2y > 0.

n

is the transform length. However, due to symmetry, only the first n/2+1 values are given in the input and output. Specified as: a fullword integer; n <= 37748736 and must be one of the values listed in Acceptable Lengths for the Transforms. For all other values specified less than 37748736, you have the option of having the next larger acceptable value returned in this argument. For details, see Providing a Correct Transform Length to ESSL.

m

is the number of sequences to be transformed. Specified as: a fullword integer; m > 0.

scale

is the scaling constant scale. See Function for its usage. Specified as: a number of the data type indicated in Table 134, where scale > 0.0 or scale < 0.0.

aux1

is the working storage for this subroutine, where:

If init <> 0, the working storage is computed.

If init = 0, the working storage is used in the computation of the Fourier transforms.

Specified as: an area of storage, containing naux1 long-precision real numbers.

naux1

is the number of doublewords in the working storage specified in aux1. Specified as: a fullword integer; naux1 >= (minimum value required for successful processing). To determine a sufficient value, use the processor-independent formulas. For all other values specified less than the minimum value, you have the option of having the minimum value returned in this argument. For details, see Using Auxiliary Storage in ESSL.

aux2

has the following meaning:

If naux2 = 0 and error 2015 is unrecoverable, aux2 is ignored.

Otherwise, it is the working storage used by this subroutine, which is available for use by the calling program between calls to this subroutine.

Specified as: an area of storage, containing naux2 long-precision real numbers. On output, the contents are overwritten.

naux2

is the number of doublewords in the working storage specified in aux2. Specified as: a fullword integer, where:

If naux2 = 0 and error 2015 is unrecoverable, SCOSF and DCOSF dynamically allocate the work area used by the subroutine. The work area is deallocated before control is returned to the calling program.

Otherwise, naux2 >= (minimum value required for successful processing). To determine a sufficient value, use the processor-independent formulas. For all other values specified less than the minimum value, you have the option of having the minimum value returned in this argument. For details, see Using Auxiliary Storage in ESSL.

On Return

y

has the following meaning, where:

If init <> 0, this argument is not used, and its contents remain unchanged.

If init = 0, this is array Y, consisting of the results of the m discrete Fourier transforms, where each Fourier transform is real and of length n. However, due to symmetry, only the first n/2+1 values are given in the output--that is, y_ki, k = 0, 1, ..., n/2 for each i = 1, 2, ..., m.

Returned as: an array of (at least) length 1+(n/2)inc1y+(m-1)inc2y, containing numbers of the data type indicated in Table 134.

aux1

is the working storage for this subroutine, where:

If init <> 0, it contains information ready to be passed in a subsequent invocation of this subroutine.

If init = 0, its contents are unchanged.

Returned as: the contents are not relevant.

Notes

1. aux1 should not be used by the calling program between calls to this subroutine with init <> 0 and init = 0. However, it can be reused after intervening calls to this subroutine with different arguments.
2. When using the ESSL SMP library, for optimal performance, the number of threads specified should be the same for init <> 0 and init = 0.
3. For optimal performance, the preferred value for inc1x and inc1y is 1. This implies that the sequences are stored with stride 1. In addition, inc2x and inc2y should be close to n/2+1.

   It is possible to specify sequences in the transposed form--that is, as rows of a two-dimensional array. In this case, inc2x (or inc2y) = 1 and inc1x (or inc1y) is equal to the leading dimension of the array. One can specify either input, output, or both in the transposed form by specifying appropriate values for the stride parameters. For selecting optimal values of inc1x and inc1y for _COSF, you should use STRIDE--Determine the Stride Value for Optimal Performance in Specified Fourier Transform Subroutines. Example 2 in the STRIDE subroutine description explains how it is used for _COSF.

   If you specify the same array for X and Y, then inc1x and inc1y must be equal, and inc2x and inc2y must be equal. In this case, output overwrites input. If m = 1, the inc2x and inc2y values are not used by the subroutine. If you specify different arrays for X and Y, they must have no common elements; otherwise, results are unpredictable. See Concepts.

Processor-Independent Formulas for SCOSF for NAUX1 and NAUX2

NAUX1 Formulas:

If n <= 16384, use naux1 = 40000.

If n > 16384, use naux1 = 20000+.30n.

NAUX2 Formulas:

If n <= 16384, use naux2 = 25000.

If n > 16384, use naux2 = 20000+.32n.

For the transposed case, where inc2x = 1 or inc2y = 1, and where n >= 252, add the following to the above storage requirements:

(n/4+257)(min(128, m)).

Processor-Independent Formulas for DCOSF for NAUX1 and NAUX2

NAUX1 Formulas:

If n <= 16384, use naux1 = 35000.

If n > 16384, use naux1 = 20000+.60n.

NAUX2 Formulas:

If n <= 16384, use naux2 = 20000.

If n > 16384, use naux2 = 20000+.64n.

For the transposed case, where inc2x = 1 or inc2y = 1, and where n >= 252, add the following to the above storage requirements:

(n/2+257)(min(128, m)).

Function

The set of m real even discrete n-point Fourier transforms of the cosine sequences of real data in array X, with results going into array Y, is expressed as follows:

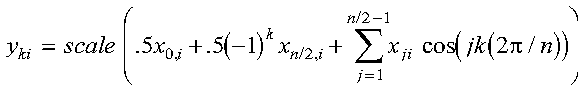
for:

k = 0, 1, ..., n/2

i = 1, 2, ..., m

where:

x_ji are elements of the sequences in array X, where each sequence contains the n/2+1 real nonredundant data x_ji, j = 0, 1, ..., n/2.

y_ki are elements of the sequences in array Y, where each sequence contains the n/2+1 real nonredundant data y_ki, k = 0, 1, ..., n/2.

scale is a scalar value.

You can obtain the inverse cosine transform by specifying scale = 4.0/n. Thus, if an X input is used with scale = 1.0, and its output is used as input on a subsequent call with scale = 4.0/n, the original X is obtained. See references [1], [4], [19], and [20].

Two invocations of this subroutine are necessary:

1. With init <> 0, the subroutine tests and initializes arguments of the program, setting up the aux1 working storage.
2. With init = 0, the subroutine checks that the initialization arguments in the aux1 working storage correspond to the present arguments, and if so, performs the calculation of the Fourier transforms.

These subroutines use a Fourier transform method with a mixed-radix capability. This provides maximum performance for your application.

Error Conditions

Resource Errors

Error 2015 is unrecoverable, naux2 = 0, and unable to allocate work area.

Computational Errors

None

Input-Argument Errors

1. n > 37748736
2. inc1x or inc1y <= 0
3. inc2x or inc2y <= 0
4. m <= 0
5. scale = 0.0
6. The subroutine has not been initialized with the present arguments.
7. The length of the transform in n is not an allowable value. Return code 1 is returned if error 2030 is recoverable.
8. naux1 is too small--that is, less than the minimum required value. Return code 1 is returned if error 2015 is recoverable.
9. Error 2015 is recoverable or naux2<>0, and naux2 is too small--that is, less than the minimum required value. Return code 1 is returned if error 2015 is recoverable.

Example 1

This example shows an input array X with a set of m cosine sequences of length n/2+1, cos(jk(2pi/n)), j = 0, 1, ..., n/2, with the single frequencies k = 0, 1, 2, 3. The Fourier transform of the cosine sequence with frequency k = 0 or n/2 has n/2 in the 0-th or n/2-th position, respectively, and zeros elsewhere. For all other k, the Fourier transform has n/4 in position k and zeros elsewhere. The arrays are declared as follows:

     REAL*4     X(0:71),Y(0:71)
     REAL*8     AUX1(414),AUX2(8960)

First, initialize AUX1 using the calling sequence shown below with INIT <> 0. Then use the same calling sequence with INIT = 0 to do the calculation.

Call Statement and Input

           INIT  X INC1X INC2X Y INC1Y INC2Y  N   M   SCALE  AUX1  NAUX1  AUX2  NAUX2
            |    |   |     |   |   |     |    |   |    |      |      |     |      |
CALL SCOSF(INIT, X , 1  , 18 , Y , 1  , 18 , 32 , 4 , SCALE, AUX1 , 414 , AUX2 , 8960)

X contains the following four sequences:

1.0000   1.0000   1.0000   1.0000
1.0000   0.9808   0.9239   0.8315
1.0000   0.9239   0.7071   0.3827
1.0000   0.8315   0.3827  -0.1951
1.0000   0.7071   0.0000  -0.7071
1.0000   0.5556  -0.3827  -0.9808
1.0000   0.3827  -0.7071  -0.9239
1.0000   0.1951  -0.9239  -0.5556
1.0000   0.0000  -1.0000   0.0000
1.0000  -0.1951  -0.9239   0.5556
1.0000  -0.3827  -0.7071   0.9239
1.0000  -0.5556  -0.3827   0.9808
1.0000  -0.7071   0.0000   0.7071
1.0000  -0.8315   0.3827   0.1951
1.0000  -0.9239   0.7071  -0.3827
1.0000  -0.9808   0.9239  -0.8315
1.0000  -1.0000   1.0000  -1.0000
 .        .        .        .

Output

Y contains the following four sequences:

16.0000  0.0000  0.0000  0.0000
 0.0000  8.0000  0.0000  0.0000
 0.0000  0.0000  8.0000  0.0000
 0.0000  0.0000  0.0000  8.0000
 0.0000  0.0000  0.0000  0.0000
 0.0000  0.0000  0.0000  0.0000
 0.0000  0.0000  0.0000  0.0000
 0.0000  0.0000  0.0000  0.0000
 0.0000  0.0000  0.0000  0.0000
 0.0000  0.0000  0.0000  0.0000
 0.0000  0.0000  0.0000  0.0000
 0.0000  0.0000  0.0000  0.0000
 0.0000  0.0000  0.0000  0.0000
 0.0000  0.0000  0.0000  0.0000
 0.0000  0.0000  0.0000  0.0000
 0.0000  0.0000  0.0000  0.0000
 0.0000  0.0000  0.0000  0.0000
  .       .       .       .

Example 2

This example shows an input array X with a set of four input spike sequences equal to the output of Example 1. This shows how you can compute the inverse of the transform in Example 1 by using scale = 4.0/n, giving as output the four sequences listed in the input for Example 1. First, initialize AUX1 using the calling sequence shown below with INIT <> 0. Then use the same calling sequence with INIT = 0 to do the calculation.

Call Statement and Input

           INIT  X INC1X INC2X Y INC1Y INC2Y  N   M   SCALE  AUX1  NAUX1  AUX2  NAUX2
            |    |   |     |   |   |     |    |   |     |     |      |     |      |
CALL SCOSF(INIT, X , 1  , 18 , Y , 1  , 18 , 32 , 4 , SCALE, AUX1 , 414 , AUX2 , 8960)

Output

Example 3

This example shows another computation using the same arguments initialized in Example 1 and using different input sequence data. The data for this example has frequencies k = 14, 15, 16, 17. Because only the sequence data has changed, initialization does not have to be done again.

Call Statement and Input

           INIT  X INC1X INC2X Y INC1Y INC2Y N   M   SCALE  AUX1  NAUX1  AUX2  NAUX2
            |   |   |     |   |   |     |    |   |     |     |      |     |      |
CALL SCOSF( 0 , X , 1  , 18 , Y , 1  , 18 , 32 , 4 , SCALE, AUX1 , 414 , AUX2 , 8960)

SCALE    =  1.0

X contains the following four sequences:

 1.0000   1.0000   1.0000   1.0000
-0.9239  -0.9808  -1.0000  -0.9808
 0.7071   0.9239   1.0000   0.9239
-0.3827  -0.8315  -1.0000  -0.8315
 0.0000   0.7071   1.0000   0.7071
 0.3827  -0.5556  -1.0000  -0.5556
-0.7071   0.3827   1.0000   0.3827
 0.9239  -0.1951  -1.0000  -0.1951
-1.0000   0.0000   1.0000   0.0000
 0.9239   0.1951  -1.0000   0.1951
-0.7071  -0.3827   1.0000  -0.3827
 0.3827   0.5556  -1.0000   0.5556
 0.0000  -0.7071   1.0000  -0.7071
-0.3827   0.8315  -1.0000   0.8315
 0.7071  -0.9239   1.0000  -0.9239
-0.9239   0.9808  -1.0000   0.9808
 1.0000  -1.0000   1.0000  -1.0000
  .        .        .        .

Output

Y contains the following four sequences:

0.0000  0.0000   0.0000  0.0000
0.0000  0.0000   0.0000  0.0000
0.0000  0.0000   0.0000  0.0000
0.0000  0.0000   0.0000  0.0000
0.0000  0.0000   0.0000  0.0000
0.0000  0.0000   0.0000  0.0000
0.0000  0.0000   0.0000  0.0000
0.0000  0.0000   0.0000  0.0000
0.0000  0.0000   0.0000  0.0000
0.0000  0.0000   0.0000  0.0000
0.0000  0.0000   0.0000  0.0000
0.0000  0.0000   0.0000  0.0000
0.0000  0.0000   0.0000  0.0000
0.0000  0.0000   0.0000  0.0000
8.0000  0.0000   0.0000  0.0000
0.0000  8.0000   0.0000  8.0000
0.0000  0.0000  16.0000  0.0000
 .       .        .       .