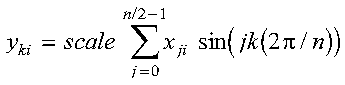

These subroutines compute a set of m real even discrete n-point Fourier transforms of sine sequences of real even data.
| X, Y, scale | Subroutine |
| Short-precision real | SSINF |
| Long-precision real | DSINF |
| Fortran | CALL SSINF | DSINF (init, x, inc1x, inc2x, y, inc1y, inc2y, n, m, scale, aux1, naux1, aux2, naux2) |
| C and C++ | ssinf | dsinf (init, x, inc1x, inc2x, y, inc1y, inc2y, n, m, scale, aux1, naux1, aux2, naux2); |
| PL/I | CALL SSINF | DSINF (init, x, inc1x, inc2x, y, inc1y, inc2y, n, m, scale, aux1, naux1, aux2, naux2); |
If init <> 0, trigonometric functions and other parameters, depending on arguments other than x, are computed and saved in aux1. The contents of x and y are not used or changed.
If init = 0, the discrete Fourier transforms of the given sequences are computed. The only arguments that may change after initialization are x, y, and aux2. All scalar arguments must be the same as when the subroutine was called for initialization with init <> 0.
Specified as: a fullword integer. It can have any value.
If init <> 0, the working storage is computed.
If init = 0, the working storage is used in the computation of the Fourier transforms.
Specified as: an area of storage, containing naux1 long-precision real numbers.
If naux2 = 0 and error 2015 is unrecoverable, aux2 is ignored.
Otherwise, it is the working storage used by this subroutine, which is available for use by the calling program between calls to this subroutine.
Specified as: an area of storage, containing naux2 long-precision real numbers. On output, the contents are overwritten.
If naux2 = 0 and error 2015 is unrecoverable, SSINF and DSINF dynamically allocate the work area used by the subroutine. The work area is deallocated before control is returned to the calling program.
Otherwise, naux2 >= (minimum value required for successful processing). To determine a sufficient value, use the processor-independent formulas. For all other values specified less than the minimum value, you have the option of having the minimum value returned in this argument. For details, see Using Auxiliary Storage in ESSL.
If init <> 0, this argument is not used, and its contents remain unchanged.
If init = 0, this is array Y, consisting of the results of the m discrete Fourier transforms, where each Fourier transform is real and of length n. However, due to symmetry, only the first n/2 values are given in the output--that is, yki, k = 0, 1, ..., n/2-1 for each i = 1, 2, ..., m.
Returned as: an array of (at least) length 1+(n / 2-1)inc1y+(m-1)inc2y, containing numbers of the data type indicated in Table 135.
If init <> 0, it contains information ready to be passed in a subsequent invocation of this subroutine.
If init = 0, its contents are unchanged.
Returned as: the contents are not relevant.
It is possible to specify sequences in the transposed form--that is, as rows of a two-dimensional array. In this case, inc2x (or inc2y) = 1 and inc1x (or inc1y) is equal to the leading dimension of the array. One can specify either input, output, or both in the transposed form by specifying appropriate values for the stride parameters. For selecting optimal values of inc1x and inc1y for _SINF, you should use STRIDE--Determine the Stride Value for Optimal Performance in Specified Fourier Transform Subroutines. Example 3 in the STRIDE subroutine description explains how it is used for _SINF.
If you specify the same array for X and Y, then inc1x and inc1y must be equal, and inc2x and inc2y must be equal. In this case, output overwrites input. If m = 1, the inc2x and inc2y values are not used by the subroutine. If you specify different arrays for X and Y, they must have no common elements; otherwise, results are unpredictable. See Concepts.
The set of m real even discrete n-point Fourier transforms of the sine sequences of real data in array X, with results going into array Y, is expressed as follows:
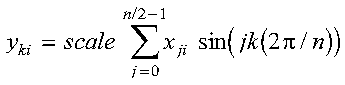
for:
where:
You can obtain the inverse sine transform by specifying scale = 4.0/n. Thus, if an X input is used with scale = 1.0, and its output is used as input on a subsequent call with scale = 4.0/n, the original X is obtained. See references [1], [4], [19], and [20].
Two invocations of this subroutine are necessary:
These subroutines use a Fourier transform method with a mixed-radix capability. This provides maximum performance for your application.
Error 2015 is unrecoverable, naux2 = 0, and unable to allocate work area.
None
This example shows an input array X with a set of m sine sequences of length n/2, sin(jk(2pi/n)), j = 0, 1, ..., n/2-1, with the single frequencies k = 1, 2, 3. The Fourier transform of the sine sequence has n/4 in position k and zeros elsewhere. The arrays are declared as follows:
REAL*4 X(0:53),Y(0:53)
REAL*8 AUX1(414),AUX2(8960)
First, initialize AUX1 using the calling sequence shown below with INIT <> 0. Then use the same calling sequence with INIT = 0 to do the calculation.
INIT X INC1X INC2X Y INC1Y INC2Y N M SCALE AUX1 NAUX1 AUX2 NAUX2
| | | | | | | | | | | | | |
CALL SSINF(INIT, X , 1 , 18 , Y , 1 , 18 , 32 , 3 , SCALE, AUX1 , 414 , AUX2 , 8960)
X contains the following three sequences:
0.0000 0.0000 0.0000 0.1951 0.3827 0.5556 0.3827 0.7071 0.9239 0.5556 0.9239 0.9808 0.7071 1.0000 0.7071 0.8315 0.9239 0.1951 0.9239 0.7071 -0.3827 0.9808 0.3827 -0.8315 1.0000 0.0000 -1.0000 0.9808 -0.3827 -0.8315 0.9239 -0.7071 -0.3827 0.8315 -0.9239 0.1951 0.7071 -1.0000 0.7071 0.5556 -0.9239 0.9808 0.3827 -0.7071 0.9239 0.1951 -0.3827 0.5556 . . . . . .
Y contains the following three sequences:
0.0000 0.0000 0.0000 8.0000 0.0000 0.0000 0.0000 8.0000 0.0000 0.0000 0.0000 8.0000 0.0000 0.0000 0.0000 0.0000 0.0000 0.0000 0.0000 0.0000 0.0000 0.0000 0.0000 0.0000 0.0000 0.0000 0.0000 0.0000 0.0000 0.0000 0.0000 0.0000 0.0000 0.0000 0.0000 0.0000 0.0000 0.0000 0.0000 0.0000 0.0000 0.0000 0.0000 0.0000 0.0000 0.0000 0.0000 0.0000 . . . . . .
This example shows an input array X with a set of three input spike sequences equal to the output of Example 1. This shows how you can compute the inverse of the transform in Example 1 by using scale = 4.0/n, giving as output the three sequences listed in the input for Example 1. First, initialize AUX1 using the calling sequence shown below with INIT <> 0. Then use the same calling sequence with INIT = 0 to do the calculation.
INIT X INC1X INC2X Y INC1Y INC2Y N M SCALE AUX1 NAUX1 AUX2 NAUX2
| | | | | | | | | | | | | |
CALL SSINF(INIT, X , 1 , 18 , Y , 1 , 18 , 32 , 3 , SCALE, AUX1 , 414 , AUX2 , 8960)
This example shows another computation using the same arguments initialized in Example 1 and using different input sequence data. The data for this example has frequencies k = 14, 15, 17. Because only the sequence data has changed, initialization does not have to be done again.
INIT X INC1X INC2X Y INC1Y INC2Y N M SCALE AUX1 NAUX1 AUX2 NAUX2
| | | | | | | | | | | | | |
CALL SSINF( 0 , X , 1 , 18 , Y , 1 , 18 , 32 , 3 , SCALE, AUX1 , 414 , AUX2 , 8960)
SCALE = 1.0
X contains the following three sequences:
0.0000 0.0000 0.0000 0.3827 0.1951 -0.1951 -0.7071 -0.3827 0.3827 0.9239 0.5556 -0.5556 -1.0000 -0.7071 0.7071 0.9239 0.8315 -0.8315 -0.7071 -0.9239 0.9239 0.3827 0.9808 -0.9808 0.8573 -1.0000 1.0000 -0.3827 0.9808 -0.9808 0.7071 -0.9239 0.9239 -0.9239 0.8315 -0.8315 1.0000 -0.7071 0.7071 -0.9239 0.5556 -0.5556 0.7071 -0.3827 0.3827 -0.3827 0.1951 -0.1951 . . . . . .
Y contains the following three sequences:
0.0000 0.0000 0.0000 0.0000 0.0000 0.0000 0.0000 0.0000 0.0000 0.0000 0.0000 0.0000 0.0000 0.0000 0.0000 0.0000 0.0000 0.0000 0.0000 0.0000 0.0000 0.0000 0.0000 0.0000 0.0000 0.0000 0.0000 0.0000 0.0000 0.0000 0.0000 0.0000 0.0000 0.0000 0.0000 0.0000 0.0000 0.0000 0.0000 8.0000 0.0000 0.0000 0.0000 8.0000 -8.0000 0.0000 0.0000 0.0000 . . . . . .