Engineering and Scientific Subroutine Library for AIX Version 3 Release 3: Guide and Reference

SCON and SCOR--Convolution or Correlation of One Sequence with One or More Sequences

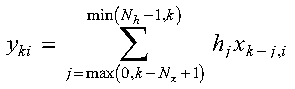
These subroutines compute the convolutions and correlations of a sequence with one or more sequences using a direct method. The input and output sequences contain short-precision real numbers.

Note:

These subroutines are considered obsolete. They are provided in ESSL only for compatibility with earlier releases. You should use SCOND, SCORD, SDCON, SDCOR, SCONF, and SCORF instead, because they provide better performance. For further details, see Convolution and Correlation Considerations.

Syntax

On Entry

init

is a flag, where:

If init <> 0, no computation is performed, error checking is performed, and the subroutine exits back to the calling program.

If init = 0, the convolutions or correlations of the sequence in h with the sequences in x are computed.

Specified as: a fullword integer. It can have any value.

h

is the array H, consisting of the sequence of length N_h to be convolved or correlated with the sequences in array X. Specified as: an array of (at least) length 1+(N_h-1)|inc1h|, containing short-precision real numbers.

inc1h

is the stride between the elements within the sequence in array H. Specified as: a fullword integer; inc1h > 0.

x

is the array X, consisting of m input sequences of length N_x, each to be convolved or correlated with the sequence in array H. Specified as: an array of (at least) length 1 + (m-1)inc2x + (N_x-1)inc1x, containing short-precision real numbers.

inc1x

is the stride between the elements within each sequence in array X. Specified as: a fullword integer; inc1x > 0.

inc2x

is the stride between the first elements of the sequences in array X. Specified as: a fullword integer; inc2x > 0.

y

See On Return.

inc1y

is the stride between the elements within each sequence in output array Y. Specified as: a fullword integer; inc1y > 0.

inc2y

is the stride between the first elements of each sequence in output array Y. Specified as: a fullword integer; inc2y > 0.

nh

is the number of elements, N_h, in the sequence in array H. Specified as: a fullword integer; N_h > 0.

nx

is the number of elements, N_x, in each sequence in array X. Specified as: a fullword integer; N_x > 0.

m

is the number of sequences in array X to be convolved or correlated. Specified as: a fullword integer; m > 0.

iy0

is the convolution or correlation index of the element to be stored in the first position of each sequence in array Y. Specified as: a fullword integer. It can have any value.

ny

is the number of elements, N_y, in each sequence in array Y. Specified as: a fullword integer; N_y > 0 for SCON and N_y >= -N_h+1 for SCOR.

aux1

is no longer used in the computation, but must still be specified as a dummy argument (for migration purposes from Version 1 of ESSL). It can have any value.

naux1

is no longer used in the computation, but must still be specified as a dummy argument (for migration purposes from Version 1 of ESSL). It can have any value.

aux2

is no longer used in the computation, but must still be specified as a dummy argument (for migration purposes from Version 1 of ESSL). It can have any value.

naux2

is no longer used in the computation, but must still be specified as a dummy argument (for migration purposes from Version 1 of ESSL). It can have any value.

On Return

y

is array Y, consisting of m output sequences of length N_y that are the result of the convolutions or correlations of the sequence in array H with the sequences in array X. Returned as: an array of (at least) length 1 + (m-1)inc2y + (N_y-1)inc1y, containing short-precision real numbers.

Notes

1. Output should not overwrite input; that is, input arrays X and H must have no common elements with output array Y. Otherwise, results are unpredictable. See Concepts.
2. When using the ESSL SMP library, for optimal performance, the number of threads specified should be the same for init <> 0 and init = 0.
3. Auxiliary storage is not needed, but the arguments aux1, naux1, aux2, and naux2 must still be specified. You can assign any values to these arguments.

Function

The convolutions and correlations of a sequence in array H with one or more sequences in array X are expressed as follows:

Convolutions for SCON:

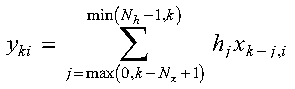
Correlations for SCOR:

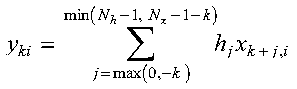
for:

k = iy0, iy0+1, ..., iy0+N_y-1

i = 1, 2, ..., m

where:

y_ki are elements of the m sequences of length N_y in array Y.

x_ki are elements of the m sequences of length N_x in array X.

h_j are elements of the sequence of length N_h in array H.

iy0 is the convolution or correlation index of the element to be stored in the first position of each sequence in array Y.

min and max select the minimum and maximum values, respectively.

It is assumed that elements outside the range of definition are zero. See references [17] and [84].

Only one invocation of this subroutine is needed:

1. You do not need to invoke the subroutine with init <> 0. If you do, however, the subroutine performs error checking, exits back to the calling program, and no computation is performed.
2. With init = 0, the subroutine performs the calculation of the convolutions or correlations.

Error Conditions

Computational Errors

None

Input-Argument Errors

1. nh, nx, ny, or m <= 0
2. inc1h, inc1x, inc2x, inc1y, or inc2y <= 0

Example 1

This example shows how to compute a convolution of a sequence in H, which is a ramp function, and three sequences in X, a triangular function and its cyclic translates. It computes the full range of nonzero values of the convolution plus two extra points, which are set to 0. The arrays are declared as follows:

     REAL*4   H(0:4999), X(0:49999), Y(0:49999)
     REAL*8   AUX1, AUX2

Call Statement and Input

          INIT  H INC1H X INC1X INC2X Y INC1Y INC2Y NH NX  M IY0 NY  AUX1 NAUX1 AUX2 NAUX2
           |    |   |   |   |     |   |   |     |    |  |  |  |   |   |     |    |     |
CALL SCON(INIT, H , 1 , X , 1 ,  10 , Y , 1 ,  15 , 4, 10, 3, 0, 15, AUX1 , 0 , AUX2 , 0)

X contains the following three sequences:

1.0  2.0  3.0
2.0  1.0  2.0
3.0  2.0  1.0
4.0  3.0  2.0
5.0  4.0  3.0
6.0  5.0  4.0
5.0  6.0  5.0
4.0  5.0  6.0
3.0  4.0  5.0
2.0  3.0  4.0

Output

Y contains the following three sequences:

 1.0   2.0   3.0
 4.0   5.0   8.0
10.0  10.0  14.0
20.0  18.0  22.0
30.0  20.0  18.0
40.0  30.0  20.0
48.0  40.0  30.0
52.0  48.0  40.0
50.0  52.0  48.0
40.0  50.0  52.0
29.0  38.0  47.0
18.0  25.0  32.0
 8.0  12.0  16.0
 0.0   0.0   0.0
 0.0   0.0   0.0

Example 2

This example shows how the output from Example 1 differs when the values for NY and inc2y are 10 rather than 15. The output is the same except that it consists of only the first 10 values produced in Example 1.

Output

Y contains the following three sequences:

 1.0   2.0   3.0
 4.0   5.0   8.0
10.0  10.0  14.0
20.0  18.0  22.0
30.0  20.0  18.0
40.0  30.0  20.0
48.0  40.0  30.0
52.0  48.0  40.0
50.0  52.0  48.0
40.0  50.0  52.0

Example 3

This example shows how the output from Example 2 differs if the value for IY0 is 3 rather than 0. The output is the same except it starts at element 3 of the convolution sequences rather than element 0.

Output

Y contains the following three sequences:

20.0  18.0  22.0
30.0  20.0  18.0
40.0  30.0  20.0
48.0  40.0  30.0
52.0  48.0  40.0
50.0  52.0  48.0
40.0  50.0  52.0
29.0  38.0  47.0
18.0  25.0  32.0
 8.0  12.0  16.0

Example 4

This example shows how to compute a correlation of a sequence in H, which is a ramp function, and three sequences in X, a triangular function and its cyclic translates. It computes the full range of nonzero values of the correlation plus two extra points, which are set to 0. The arrays are declared as follows:

     REAL*4   H(0:4999), X(0:49999), Y(0:49999)
     REAL*8   AUX1, AUX2

Call Statement and Input

          INIT  H INC1H X INC1X INC2X Y INC1Y INC2Y NH NX  M IY0  NY  AUX1  NAUX1 AUX2 NAUX2
           |    |   |   |   |     |   |   |     |   |  |   |   |   |   |      |    |     |
CALL SCOR(INIT, H , 1 , X , 1  , 10 , Y , 1  , 15 , 4, 10, 3, -3, 15, AUX1 ,  0 , AUX2 , 0)

X contains the following three sequences:

1.0  2.0  3.0
2.0  1.0  2.0
3.0  2.0  1.0
4.0  3.0  2.0
5.0  4.0  3.0
6.0  5.0  4.0
5.0  6.0  5.0
4.0  5.0  6.0
3.0  4.0  5.0
2.0  3.0  4.0

Output

Y contains the following three sequences:

 4.0   8.0  12.0
11.0  10.0  17.0
20.0  15.0  16.0
30.0  22.0  18.0
40.0  30.0  22.0
50.0  40.0  30.0
52.0  50.0  40.0
48.0  52.0  50.0
40.0  48.0  52.0
30.0  40.0  48.0
16.0  22.0  28.0
 7.0  10.0  13.0
 2.0   3.0   4.0
 0.0   0.0   0.0
 0.0   0.0   0.0

Example 5

This example shows how the output from Example 4 differs when the values for NY and INC2Y are 10 rather than 15. The output is the same except that it consists of only the first 10 values produced in Example 4.

Output

Y contains the following three sequences:

 4.0   8.0  12.0
11.0  10.0  17.0
20.0  15.0  16.0
30.0  22.0  18.0
40.0  30.0  22.0
50.0  40.0  30.0
52.0  50.0  40.0
48.0  52.0  50.0
40.0  48.0  52.0
30.0  40.0  48.0

Example 6

This example shows how the output from Example 5 differs if the value for IY0 is 0 rather than -3. The output is the same except it starts at element 0 of the correlation sequences rather than element -3.

Output

Y contains the following three sequences:

30.0  22.0  18.0
40.0  30.0  22.0
50.0  40.0  30.0
52.0  50.0  40.0
48.0  52.0  50.0
40.0  48.0  52.0
30.0  40.0  48.0
16.0  22.0  28.0
 7.0  10.0  13.0
 2.0   3.0   4.0