Engineering and Scientific Subroutine Library for AIX Version 3 Release 3: Guide and Reference

SCOND and SCORD--Convolution or Correlation of One Sequence with Another Sequence Using a Direct Method

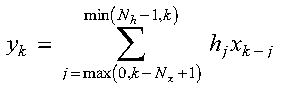
These subroutines compute the convolution and correlation of a sequence with another sequence using a direct method. The input and output sequences contain short-precision real numbers.

Notes:

1. These subroutines compute the convolution and correlation using direct methods. In most cases, these subroutines provide better performance than using SCON or SCOR, if you determine that SCON or SCOR would have used a direct method for its computation. For information on how to make this determination, see reference [4].

2. For long-precision data, you should use DDCON or DDCOR with the decimation rate, id, equal to 1.

Syntax

On Entry

h

is the array H, consisting of the sequence of length N_h to be convolved or correlated with the sequence in array X. Specified as: an array of (at least) length 1+(N_h-1)|inch|, containing short-precision real numbers.

inch

is the stride between the elements within the sequence in array H. Specified as: a fullword integer; inch > 0 or inch < 0.

x

is the array X, consisting of the input sequence of length N_x, to be convolved or correlated with the sequence in array H. Specified as: an array of (at least) length 1+(N_x-1)|incx|, containing short-precision real numbers.

incx

is the stride between the elements within the sequence in array X. Specified as: a fullword integer; incx > 0 or incx < 0.

y

See On Return.

incy

is the stride between the elements within the sequence in output array Y. Specified as: a fullword integer; incy > 0 or incy < 0.

nh

is the number of elements, N_h, in the sequence in array H. Specified as: a fullword integer; N_h > 0.

nx

is the number of elements, N_x, in the sequence in array X. Specified as: a fullword integer; N_x > 0.

iy0

is the convolution or correlation index of the element to be stored in the first position of the sequence in array Y. Specified as: a fullword integer. It can have any value.

ny

is the number of elements, N_y, in the sequence in array Y. Specified as: a fullword integer; N_y > 0.

On Return

y

is the array Y of length N_y, consisting of the output sequence that is the result of the convolution or correlation of the sequence in array H with the sequence in array X. Returned as: an array of (at least) length 1+(N_y-1)|incy|, containing short-precision real numbers.

Notes

1. Output should not overwrite input--that is, input arrays X and H must have no common elements with output array Y. Otherwise, results are unpredictable. See Concepts.
2. If iy0 and ny are such that output outside the basic range is needed, where the basic range is 0 <= k <= (nh+nx-2) for SCOND and (-nh+1) <= k <= (nx-1) for SCORD, the subroutine stores zeros using scalar code. It is not efficient to store many zeros in this manner. It is more efficient to set iy0 and ny so that the output is produced within the above range of k values.

Function

The convolution and correlation of a sequence in array H with a sequence in array X are expressed as follows:

Convolution for SCOND:

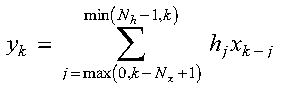
Correlation for SCORD:

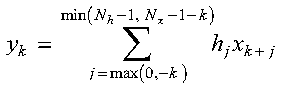
for k = iy0, iy0+1, ..., iy0+N_y-1

where:

y_k are elements of the sequence of length N_y in array Y.

x_k are elements of the sequence of length N_x in array X.

h_j are elements of the sequence of length N_h in array H.

iy0 is the convolution or correlation index of the element to be stored in the first position of each sequence in array Y.

min and max select the minimum and maximum values, respectively.

It is assumed that elements outside the range of definition are zero. See reference [4].

Special Usage

SCORD can also perform the functions of SCON and SACOR; that is, it can compute convolutions and autocorrelations. To compute a convolution, you must specify a negative stride for H (see Example 9). To compute the autocorrelation, you must specify the two input sequences to be the same (see Example 10). In fact, you can also compute the autoconvolution by using both of these techniques together, letting the two input sequences be the same, and specifying a negative stride for the first input sequence.

Error Conditions

Computational Errors

None

Input-Argument Errors

1. nh, nx, or ny <= 0
2. inch, incx, or incy = 0

Example 1

This example shows how to compute a convolution of a sequence in H with a sequence in X, where both sequences are ramp functions.

Call Statement and Input

            H  INCH  X  INCX  Y  INCY  NH  NX IY0  NY
            |   |    |   |    |   |    |   |   |   |
CALL SCOND( H , 1  , X , 1  , Y , 1  , 4 , 8 , 0 , 11 )
 
H        =  (1.0, 2.0, 3.0, 4.0)
X        =  (11.0, 12.0, 13.0, 14.0, 15.0, 16.0, 17.0, 18.0)

Output

Y        =  (11.0, 34.0, 70.0, 120.0, 130.0, 140.0, 150.0, 160.0,
             151.0, 122.0, 72.0)

Example 2

This example shows how the output from Example 1 differs when the value for IY0 is -2 rather than 0, and NY is 15 rather than 11. The output has two zeros at the beginning and end of the sequence, for points outside the range of nonzero output.

Call Statement and Input

            H  INCH  X  INCX  Y  INCY  NH  NX  IY0  NY
            |   |    |   |    |   |    |   |    |   |
CALL SCOND( H , 1  , X , 1  , Y , 1  , 4 , 8 , -2 , 15 )
 
H        =  (1.0, 2.0, 3.0, 4.0)
X        =  (11.0, 12.0, 13.0, 14.0, 15.0, 16.0, 17.0, 18.0)

Output

Y        =  (0.0, 0.0, 11.0, 34.0, 70.0, 120.0, 130.0, 140.0, 150.0,
             160.0, 151.0, 122.0, 72.0, 0.0, 0.0)

Example 3

This example shows how the same output as Example 1 can be obtained when H and X are interchanged, because the convolution is symmetric in H and X. (The arguments are switched in the calling sequence.)

Call Statement and Input

            H  INCH  X  INCX  Y  INCY  NH  NX IY0  NY
            |   |    |   |    |   |    |   |   |   |
CALL SCOND( X , 1  , H , 1  , Y , 1  , 4 , 8 , 0 , 11 )
 
H        =  (1.0, 2.0, 3.0, 4.0)
X        =  (11.0, 12.0, 13.0, 14.0, 15.0, 16.0, 17.0, 18.0)

Output

Y        =  (11.0, 34.0, 70.0, 120.0, 130.0, 140.0, 150.0, 160.0,
             151.0, 122.0, 72.0)

Example 4

This example shows how the output from Example 1 differs when a negative stride is specified for the sequence in H. By reversing the H sequence, the correlation is computed.

Call Statement and Input

            H  INCH  X  INCX  Y  INCY  NH  NX IY0  NY
            |    |   |   |    |   |    |   |   |   |
CALL SCOND( H , -1 , X , 1  , Y , 1  , 4 , 8 , 0 , 11 )
 
H        =  (1.0, 2.0, 3.0, 4.0)
X        =  (11.0, 12.0, 13.0, 14.0, 15.0, 16.0, 17.0, 18.0)

Output

Y        =  (44.0, 81.0, 110.0, 130.0, 140.0, 150.0, 160.0, 170.0,
             104.0, 53.0, 18.0)

Example 5

This example shows how to compute the autoconvolution of a sequence by letting the two input sequences for H and X be the same. (X is specified for both arguments in the calling sequence.)

Call Statement and Input

            H  INCH  X  INCX  Y  INCY NH  NX IY0  NY
            |   |   |   |    |   |    |   |   |   |
CALL SCOND( X , 1 , X , 1  , Y , 1  , 4 , 4 , 0 , 7 )
 
X        =  (11.0, 12.0, 13.0, 14.0)

Output

Y        =  (121.0, 264.0, 430.0, 620.0, 505.0, 364.0, 196.0)

Example 6

This example shows how to compute a correlation of a sequence in H with a sequence in X, where both sequences are ramp functions.

Call Statement and Input

            H  INCH  X  INCX  Y  INCY NH  NX   IY0  NY
            |   |    |   |    |   |    |   |    |   |
CALL SCORD( H , 1  , X , 1  , Y , 1  , 4 , 8 , -3 , 11 )
 
H        =  (1.0, 2.0, 3.0, 4.0)
X        =  (11.0, 12.0, 13.0, 14.0, 15.0, 16.0, 17.0, 18.0)

Output

Y        =  (44.0, 81.0, 110.0, 130.0, 140.0, 150.0, 160.0, 170.0,
             104.0, 53.0, 18.0)

Example 7

This example shows how the output from Example 6 differs when the value for IY0 is -5 rather than -3 and NY is 15 rather than 11. The output has two zeros at the beginning and end of the sequence, for points outside the range of nonzero output.

Call Statement and Input

            H  INCH  X  INCX  Y  INCY NH  NX   IY0  NY
            |   |    |   |    |   |    |   |    |   |
CALL SCORD( H , 1  , X , 1  , Y , 1  , 4 , 8 , -5 , 15 )
 
H        =  (1.0, 2.0, 3.0, 4.0)
X        =  (11.0, 12.0, 13.0, 14.0, 15.0, 16.0, 17.0, 18.0)

Output

Y        =  (0.0, 0.0, 44.0, 81.0, 110.0, 130.0, 140.0, 150.0, 160.0,
             170.0, 104.0, 53.0, 18.0, 0.0, 0.0)

Example 8

This example shows how the output from Example 6 differs when H and X are interchanged (in the calling sequence). The output sequence is the reverse of that in Example 6. To get the full range of output, IY0 is set to -NX+1.

Call Statement and Input

            H  INCH  X  INCX  Y  INCY NH  NX   IY0  NY
            |   |    |   |    |   |    |   |    |   |
CALL SCORD( X , 1  , H , 1  , Y , 1  , 4 , 8 , -7 , 11 )
 
H        =  (1.0, 2.0, 3.0, 4.0)
X        =  (11.0, 12.0, 13.0, 14.0, 15.0, 16.0, 17.0, 18.0)

Output

Y        =  (18.0, 53.0, 104.0, 170.0, 160.0, 150.0, 140.0, 130.0,
             110.0, 81.0, 44.0)

Example 9

This example shows how the output from Example 6 differs when a negative stride is specified for the sequence in H. By reversing the H sequence, the convolution is computed.

Call Statement and Input

            H  INCH  X  INCX  Y  INCY  NH  NX  IY0  NY
            |    |   |   |    |   |    |   |    |   |
CALL SCORD( H , -1 , X , 1  , Y , 1  , 4 , 8 , -3 , 11 )
 
H        =  (1.0, 2.0, 3.0, 4.0)
X        =  (11.0, 12.0, 13.0, 14.0, 15.0, 16.0, 17.0, 18.0)

Output

Y        =  (11.0, 34.0, 70.0, 120.0, 130.0, 140.0, 150.0, 160.0,
             151.0, 122.0, 72.0)

Example 10

This example shows how to compute the autocorrelation of a sequence by letting the two input sequences for H and X be the same. (X is specified for both arguments in the calling sequence.)

Call Statement and Input

            H  INCH  X  INCX  Y  INCY  NH  NX  IY0  NY
            |   |    |   |    |   |    |   |    |   |
CALL SCORD( X , 1  , X , 1  , Y , 1  , 4 , 4 , -3 , 7 )
 
X        =  (11.0, 12.0, 13.0, 14.0)

Output

Y        =  (154.0, 311.0, 470.0, 630.0, 470.0, 311.0, 154.0)