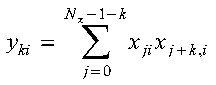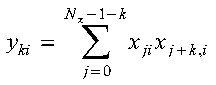Engineering and Scientific Subroutine Library for AIX Version 3 Release 3: Guide and Reference

SACOR--Autocorrelation of One or More Sequences

This subroutine computes the autocorrelations of one or more sequences using a direct method. The input and output sequences contain short-precision real numbers.

Note:

This subroutine is considered obsolete. It is provided in ESSL only for compatibility with earlier releases. You should use SCORD, SDCOR, SCORF and SACORF instead, because they provide better performance. For further details, see reference [4].

Syntax

On Entry

init

is a flag, where:

If init <> 0, no computation is performed, error checking is performed, and the subroutine exits back to the calling program.

If init = 0, the autocorrelations of the sequence in x are computed.

Specified as: a fullword integer. It can have any value.

x

is the array X, consisting of m input sequences of length N_x, to be autocorrelated. Specified as: an array of (at least) length 1+(N_x-1)inc1x+(m-1)inc2x, containing short-precision real numbers.

inc1x

is the stride between the elements within each sequence in array X. Specified as: a fullword integer; inc1x > 0.

inc2x

is the stride between the first elements of the sequences in array X. Specified as: a fullword integer; inc2x > 0.

y

See On Return.

inc1y

is the stride between the elements within each sequence in output array Y. Specified as: a fullword integer; inc1y > 0.

inc2y

is the stride between the first elements of each sequence in output array Y. Specified as: a fullword integer; inc2y > 0.

nx

is the number of elements, N_x, in each sequence in array X. Specified as: a fullword integer; N_x > 0.

m

is the number of sequences in array X to be correlated. Specified as: a fullword integer; m > 0.

ny

is the number of elements, N_y, in each sequence in array Y. Specified as: a fullword integer; N_y > 0.

aux1

is no longer used in the computation, but must still be specified as a dummy argument (for migration purposes from Version 1 of ESSL). It can have any value.

naux1

is no longer used in the computation, but must still be specified as a dummy argument (for migration purposes from Version 1 of ESSL). It can have any value.

aux2

is no longer used in the computation, but must still be specified as a dummy argument (for migration purposes from Version 1 of ESSL). It can have any value.

naux2

is no longer used in the computation, but must still be specified as a dummy argument (for migration purposes from Version 1 of ESSL). It can have any value.

On Return

y

is array Y, consisting of m output sequences of length N_y that are the autocorrelation functions of the sequences in array X. Returned as: an array of (at least) length 1 + (N_y-1)inc1y + (m-1)inc2y, containing short-precision real numbers.

Notes

1. Output should not overwrite input; that is, input arrays X and H must have no common elements with output array Y. Otherwise, results are unpredictable. See Concepts.
2. When using the ESSL SMP library, for optimal performance, the number of threads specified should be the same for init <> 0 and init = 0.
3. Auxiliary storage is not needed, but the arguments aux1, naux1, aux2, and naux2 must still be specified. You can assign any values to these arguments.

Function

The autocorrelations of the sequences in array X are expressed as follows:

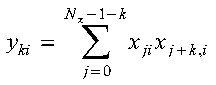
for:

k = 0, 1, ..., N_y-1

i = 1, 2, ..., m

where:

y_ki are elements of the m sequences of length N_y in array Y.

x_ji and x_j+k,i are elements of the m sequences of length N_x in array X.

See references [17] and [84].

Only one invocation of this subroutine is needed:

1. You do not need to invoke the subroutine with init <> 0. If you do, however, the subroutine performs error checking, exits back to the calling program, and no computation is performed.
2. With init = 0, the subroutine performs the calculation of the convolutions or correlations.

Error Conditions

Computational Errors

None

Input-Argument Errors

1. nx, ny, or m <= 0
2. inc1x, inc2x, inc1y, or inc2y <= 0 (or incompatible)

Example 1

This example shows how to compute an autocorrelation for three short sequences in array X, where the input sequence length NX is equal to the output sequence length NY. This gives all nonzero autocorrelation values.

The arrays are declared as follows:

     REAL*4   X(0:49999), Y(0:49999)
     REAL*8   AUX1, AUX2

Call Statement and Input

           INIT  X INC1X INC2X Y INC1Y INC2Y NX  M   NY  AUX1 NAUX1 AUX2   NAUX2
            |    |   |     |   |   |     |   |   |   |    |     |    |       |
CALL SACOR(INIT, X , 1  ,  7 , Y , 1  ,  7 , 7 , 3 , 7 , AUX1 , 0 , AUX2 ,   0)

X contains the following three sequences:

1.0  2.0  3.0
2.0  1.0  2.0
3.0  2.0  1.0
4.0  3.0  2.0
4.0  4.0  3.0
3.0  4.0  4.0
2.0  3.0  4.0

Output

Y contains the following three sequences:

59.0  59.0  59.0
54.0  50.0  44.0
43.0  39.0  30.0
29.0  27.0  24.0
16.0  18.0  21.0
 7.0  11.0  20.0
 2.0   6.0  12.0

Example 2

This example shows how the output from Example 1 differs when the values for NY and INC2Y are 9 rather than 7. This shows that when NY is greater than NX, the output array is longer, and that part is filled with zeros.

Output

Y contains the following three sequences:

59.0  59.0  59.0
54.0  50.0  44.0
43.0  39.0  30.0
29.0  27.0  24.0
16.0  18.0  21.0
 7.0  11.0  20.0
 2.0   6.0  12.0
 0.0   0.0   0.0
 0.0   0.0   0.0

Example 3

This example shows how the output from Example 1 differs when the value for NY is 5 rather than 7. Also, the values for INC1X and INC1Y are 3, and the values for INC2X and INC2Y are 1 rather than 7. This shows that when NY is less than NX, the output array is shortened.

Output

Y contains the following three sequences:

59.0  59.0  59.0
54.0  50.0  44.0
43.0  39.0  30.0
29.0  27.0  24.0
16.0  18.0  21.0