Engineering and Scientific Subroutine Library for AIX Version 3 Release 3: Guide and Reference

SDCON, DDCON, SDCOR, and DDCOR--Convolution or Correlation with Decimated Output Using a Direct Method

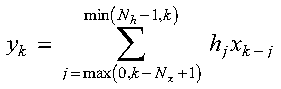
These subroutines compute the convolution and correlation of a sequence with another sequence, with decimated output, using a direct method.

Table 142. Data Types

Note:

These subroutines are the short- and long-precision equivalents of SCOND and SCORD when the decimation interval id is equal to 1. Because there is no long-precision version of SCOND and SCORD, you can use DDCON and DDCOR, respectively, with decimation interval id = 1 to perform the same function.

Syntax

On Entry

h

is the array H, consisting of the sequence of length N_h to be convolved or correlated with the sequence in array X. Specified as: an array of (at least) length 1+(N_h-1)|inch|, containing numbers of the data type indicated in Table 142.

inch

is the stride between the elements within the sequence in array H. Specified as: a fullword integer; inch > 0 or inch < 0.

x

is the array X, consisting of the input sequence of length N_x, to be convolved or correlated with the sequence in array H. Specified as: an array of (at least) length 1+(N_x-1)|incx|, containing numbers of the data type indicated in Table 142.

incx

is the stride between the elements within the sequence in array X. Specified as: a fullword integer; incx > 0 or incx < 0.

y

See On Return.

incy

is the stride between the elements within the sequence in output array Y. Specified as: a fullword integer; incy > 0 or incy < 0.

nh

is the number of elements, N_h, in the sequence in array H. Specified as: a fullword integer; N_h > 0.

nx

is the number of elements, N_x, in the sequence in array X. Specified as: a fullword integer; N_x > 0.

iy0

is the convolution or correlation index of the element to be stored in the first position of the sequence in array Y. Specified as: a fullword integer. It can have any value.

ny

is the number of elements, N_y, in the sequence in array Y. Specified as: a fullword integer; N_y > 0.

id

is the decimation interval id for the output sequence in array Y; that is, every id-th value of the convolution or correlation is produced. Specified as: a fullword integer; id > 0.

On Return

y

is the array Y of length N_y, consisting of the output sequence that is the result of the convolution or correlation of the sequence in array H with the sequence in array X, given for every id-th value in the convolution or correlation.

Returned as: an array of (at least) length 1+(N_y-1)|incy|, containing numbers of the data type indicated in Table 142.

Notes

1. If you specify the same array for X and Y, the following conditions must be true: incx = incy, incx > 0, incy > 0, id = 1, and iy0 >= N_h-1 for _DCON and iy0 >= 0 for _DCOR. In this case, output overwrites input. In all other cases, output should not overwrite input; that is, input arrays X and H must have no common elements with output array Y. Otherwise, results are unpredictable. See Concepts.
2. If iy0 and ny are such that output outside the basic range is needed, where the basic range is 0 <= k <= (nh+nx-2) for SDCON and DDCON and is (-nh+1) <= k <= (nx-1) for SDCOR and DDCOR, the subroutine stores zeros using scalar code. It is not efficient to store many zeros in this manner. If you anticipate that this will happen, you may want to adjust iy0 and ny, so the subroutine computes only for k in the above range, or use the ESSL subroutine SSCAL or DSCAL to store the zeros, so you achieve better performance.

Function

The convolution and correlation of a sequence in array H with a sequence in array X, with decimated output, are expressed as follows:

Convolution for SDCON and DDCON:

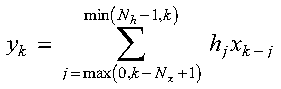
Correlation for SDCOR and DDCOR:

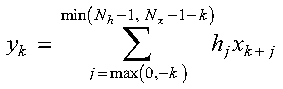
for k = iy0, iy0+id, iy0+(2)id, ..., iy0+(N_y-1)id

where:

y_k are elements of the sequence of length N_y in array Y.

x_k are elements of the sequence of length N_x in array X.

h_j are elements of the sequence of length N_h in array H.

iy0 is the convolution or correlation index of the element to be stored in the first position of the sequence in array Y.

min and max select the minimum and maximum values, respectively.

It is assumed that elements outside the range of definition are zero. See reference [4].

Special Usage

SDCON and DDCON can also perform a correlation, autoconvolution, or autocorrelation. To compute a correlation, you must specify a negative stride for H. To compute the autoconvolution, you must specify the two input sequences to be the same. You can also compute the autocorrelation by using both of these techniques together, letting the two input sequences be the same, and specifying a negative stride for the first input sequence. For examples of this, see the examples for SCOND on page "Example 1". Because SCOND and SDCON are functionally the same, their results are the same as long as the decimation interval id = 1 for SDCON.

SDCOR and DDCOR can also perform a convolution, autocorrelation, or autoconvolution. To compute a convolution, you must specify a negative stride for H. To compute the autocorrelation, you must specify the two input sequences to be the same. You can also compute the autoconvolution by using both of these techniques together, letting the two input sequences be the same and specifying a negative stride for the first input sequence. For examples of these, see the examples for SCORD on page "Example 6". Because SCORD and SDCOR are functionally the same, their results are the same as long as the decimation interval id = 1 for SDCOR.

Error Conditions

Computational Errors

None

Input-Argument Errors

1. nh, nx, or ny <= 0
2. inch, incx, or incy = 0
3. id <= 0

Example 1

This example shows how to compute a convolution of a sequence in H with a sequence in X, where both sequences are ramp functions. It shows how a decimated output can be obtained, using the same input as Example 1 for SCOND and using a decimation interval ID = 2.

Note:

For further examples of use, see the examples for SCOND on page "Example 1". Because SCOND and SDCON are functionally the same, their results are the same as long as the decimation interval ID = 1 for SDCON.

Call Statement and Input

            H  INCH  X  INCX  Y  INCY  NH  NX IY0  NY  ID
            |   |    |   |    |   |    |   |   |   |   |
CALL SDCON( H , 1  , X , 1  , Y , 1  , 4 , 8 , 0 , 6 , 2 )
 
H        =  (1.0, 2.0, 3.0, 4.0)
X        =  (11.0, 12.0, 13.0, 14.0, 15.0, 16.0, 17.0, 18.0)

Output

Y        =  (11.0, 70.0, 130.0, 150.0, 151.0, 72.0)

Example 2

This example shows how to compute a correlation of a sequence in H with a sequence in X, where both sequences are ramp functions. It shows how a decimated output can be obtained, using the same input as Example 6 for SCORD and using a decimation interval ID = 2.

Note:

For further examples of use, see the examples for SCORD on page "Example 6". Because SCORD and SDCOR are functionally the same, their results are the same as long as the decimation interval ID = 1 for SDCOR.

Call Statement and Input

            H  INCH  X  INCX  Y  INCY  NH  NX  IY0  NY  ID
            |   |    |   |    |   |    |   |    |   |   |
CALL SDCOR( H , 1  , X , 1  , Y , 1  , 4 , 8 , -3 , 6 , 2 )
 
H        =  (1.0, 2.0, 3.0, 4.0)
X        =  (11.0, 12.0, 13.0, 14.0, 15.0, 16.0, 17.0, 18.0)

Output

Y        =  (44.0, 110.0, 140.0, 160.0, 104.0, 18.0)

Example 3

This example shows how to compute the same function as computed in Example 1 for SCOND. The input sequences and arguments are the same as that example, except a decimation interval ID = 1 is specified here for SDCON.

Call Statement and Input

            H  INCH  X  INCX  Y  INCY  NH  NX IY0  NY   ID
            |   |    |   |    |   |    |   |   |    |   |
CALL SDCON( H , 1  , X , 1  , Y , 1  , 4 , 8 , 0 , 11 , 1 )
 
H        =  (1.0, 2.0, 3.0, 4.0)
X        =  (11.0, 12.0, 13.0, 14.0, 15.0, 16.0, 17.0, 18.0)

Output

Y        =  (11.0, 34.0, 70.0, 120.0, 130.0, 140.0, 150.0, 160.0,
             151.0, 122.0, 72.0)