Engineering and Scientific Subroutine Library for AIX Version 3 Release 3: Guide and Reference

SURXOR and DURXOR--Generate a Vector of Long Period Uniformly Distributed Random Numbers

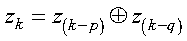
These subroutines generate a vector x of uniform [0,1) pseudo-random numbers, using the Tausworthe exclusive-or algorithm.

Table 170. Data Types

Syntax

On Entry

iseed

has the following meaning, where:

If iseed <> 0, iseed is the initial value used to generate the random numbers. You specify iseed <> 0 when you call this subroutine for the first time or when you changed vseed between calls to this subroutine.

If iseed = 0, vseed is used to generate the random numbers, where vseed was initialized by an earlier call to this subroutine. ESSL assumes you have not changed vseed between calls to this subroutine, when you specify iseed = 0.

Specified as: a fullword integer, as indicated in Table 170.

n

is the number of random numbers to be generated. Specified as: a fullword integer; n >= 0.

x

See On Return.

vseed

is the work area used by this subroutine and has the following meaning, where:

If iseed <> 0, vseed is not used for input. The work area can contain anything.

If iseed = 0, vseed contains the seed vector generated by a preceding call to this subroutine. vseed is used in this computation to generate the new random numbers. It should not be changed between calls to this subroutine.

Specified as: a one-dimensional array of (at least) length 10000, containing numbers of the data type indicated in Table 170.

On Return

iseed

is set to 0 for subsequent calls to SURXOR or DURXOR. Returned as: a fullword integer, as indicated in Table 170.

x

is a vector of length n, containing the uniform pseudo-random numbers with the following values: 0 <= x < 1. Returned as: a one-dimensional array of (at least) length n, containing numbers of the data type indicated in Table 170.

vseed

is the work area used by these subroutines, containing the new seed that is to be used in subsequent calls to this subroutine. Returned as: a one-dimensional array of (at least) length 10000, containing numbers of the data type indicated in Table 170.

Notes

1. You can generate the same vector x of random numbers by starting over and specifying your original nonzero iseed value.
2. Multiple calls to these subroutines with mixed sizes generate the same sequence of numbers as a single call the total length, assuming you specify the same initial iseed in both cases. For example, you can generate the same vector x of random numbers by calling this subroutine twice and specifying n = 10 or by calling this subroutine once and specifying n = 20. You need to specify the same iseed in the initial call in both cases, and iseed = 0 in the second call with n = 10.
3. Vector x must have no common elements with the storage area specified for vseed; otherwise, results are unpredictable.
4. In your C program, argument iseed must be passed by reference.

Function

The pseudo-random numbers uniformly distributed in the interval [0,1) are generated using the Tausworthe exclusive-or algorithm. This is based on a linear-feedback shift-register sequence. The very long period of the generator, 2¹²⁷⁹-1, makes it useful in modern statistical simulations where the shorter period of other generators could be exhausted during a single run. If you need a large number of random numbers, you can use these subroutines, because with this generator you do not request more than a small percentage of the entire period of the generator.

This generator is based on two feedback positions to generate a new binary digit:

where:

p > q

k = 1, 2, ...

z is a bit vector.

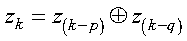
and where:

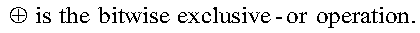
For details, see references [53], [74], and [94]. The values of p and q are selected according to the criteria stated in reference [100].

The algorithm initializes a seed vector of length p, starting with iseed. The seed vector is stored in vseed for use in subsequent calls to this subroutine with iseed = 0.

If n is 0, no computation is performed, and the initial seed is unchanged.

Special Usage

For some specialized applications, if you need multiple sources of random numbers, you can specify different vseed areas, which are initialized with different seeds on multiple calls to this subroutine. You then get multiple sequences of the random number sequence provided by the generator that are sufficiently far apart for most purposes.

Error Conditions

Computational Errors

None.

Input-Argument Errors

1. n < 0
2. iseed = 0 and vseed does not contain valid data.

Example 1

This example shows a call to SURXOR to generate 10 random numbers.

Call Statement and Input

             ISEED    N   X   VSEED
               |      |   |     |
CALL SURXOR( ISEED , 10 , X , VSEED )
 
ISEED    =  137

Output

ISEED    =  0
 
X        =  (0.6440868,
             0.5105118,
             0.4878680,
             0.3209075,
             0.6624528,
             0.2499877,
             0.0056630,
             0.7329214,
             0.7486335,
             0.8050517)

Example 2

This example shows a call to SURXOR to generate 10 random numbers. This example specifies iseed = 0 and uses the vseed output generated from Example 1.

Call Statement and Input

             ISEED    N   X   VSEED
               |      |   |     |
CALL SURXOR( ISEED , 10 , X , VSEED )
 
ISEED    =  0

Output

ISEED    =  0
 
X        =  (0.9930249,
             0.0441873,
             0.6891295,
             0.3101060,
             0.6324178,
             0.3299408,
             0.3553145,
             0.0100013,
             0.0214620,
             0.8059390)

Example 3

This example shows a call to DURXOR to generate 20 random numbers. This sequence of numbers generated are like those generated in Examples 1 and 2.

Call Statement and Input

             ISEED    N   X   VSEED
               |      |   |     |
CALL DURXOR( ISEED , 20 , X , VSEED )
 
ISEED    =  137

Output

ISEED    =  0
 
X        =   (0.64408693438956721,
              0.51051182536460882,
              0.48786801310787142,
              0.32090755617007050,
              0.66245283144861666,
              0.24998782843358081,
              0.00566308101257373,
              0.73292147005172925,
              0.74863359794102236,
              0.80505169697755319,
              0.99302499462139138,
              0.04418740640269125,
              0.68912952155409579,
              0.31010611495627916,
              0.63241786342211936,
              0.32994081459690583,
              0.35531452631408911,
              0.01000134413132581,
              0.02146199494672940,
              0.80593898487597615)