IBM Books

Engineering and Scientific Subroutine Library for AIX Version 3 Release 3: Guide and Reference

SASUM, DASUM, SCASUM, and DZASUM--Sum of the Magnitudes of the Elements in a Vector

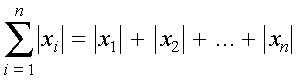
SASUM and DASUM compute the sum of the absolute values of the elements in vector x. SCASUM and DZASUM compute the sum of the absolute values of the real and imaginary parts of the elements in vector x.

Table 40. Data Types

x Result Subprogram
Short-precision real Short-precision real SASUM
Long-precision real Long-precision real DASUM
Short-precision complex Short-precision real SCASUM
Long-precision complex Long-precision real DZASUM

Syntax

Fortran SASUM | DASUM | SCASUM | DZASUM (n, x, incx)
C and C++ sasum | dasum | scasum | dzasum (n, x, incx);
PL/I SASUM | DASUM | SCASUM | DZASUM (n, x, incx);

On Entry

n
is the number of elements in vector x. Specified as: a fullword integer; n >= 0.

x
is the vector x of length n. Specified as: a one-dimensional array of (at least) length 1+(n-1)|incx|, containing numbers of the data type indicated in Table 40.

incx
is the stride for vector x. Specified as: a fullword integer. It can have any value.

On Return

Function value
is the result of the summation. Returned as: a number of the data type indicated in Table 40.

Note

Declare this function in your program as returning a value of the type indicated in Table 40.

Function

SASUM and DASUM compute the sum of the absolute values of the elements of x, which is expressed as follows:



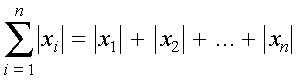
Summation Graphic

SCASUM and DZASUM compute the sum of the absolute values of the real and imaginary parts of the elements of x, which is expressed as follows:



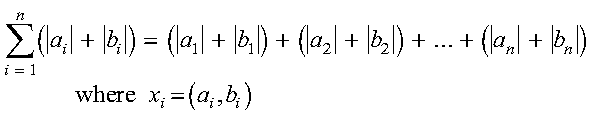
Summation Graphic

See reference [79]. The result is returned as a function value. If n is 0, then 0.0 is returned as the value of the function. For SASUM and SCASUM, intermediate results are accumulated in long precision.

Error Conditions

Computational Errors

None

Input-Argument Errors

n < 0

Example 1

This example shows a vector, x, with a stride of 1.

Function Reference and Input
              N   X  INCX
              |   |   |
SUMM = SASUM( 7 , X , 1  )
 
X        =  (1.0, -3.0, -6.0, 7.0, 5.0, 2.0, -4.0)

Output
SUMM     =  28.0

Example 2

This example shows a vector, x, with a stride greater than 1.

Function Reference and Input
              N   X  INCX
              |   |   |
SUMM = SASUM( 4 , X , 2  )
 
X        =  (1.0, . , -6.0, . , 5.0, . , -4.0)

Output
SUMM     =  16.0

Example 3

This example shows a vector, x, with negative stride. Processing begins at element X(7), which is -4.0.

Function Reference and Input
              N   X   INCX
              |   |    |
SUMM = SASUM( 4 , X , -2  )
 
X        =  (1.0, . , -6.0, . , 5.0, . , -4.0)

Output
SUMM     =  16.0

Example 4

This example shows a vector, x, with a stride of 0. The result in SUMM is nx1.

Function Reference and Input
              N   X  INCX
              |   |   |
SUMM = SASUM( 7 , X , 0  )
 
X        =  (-2.0, . , . , . , . , . , .)

Output
SUMM     =  14.0

Example 5

This example shows a vector, x, containing complex numbers and having a stride of 1.

Function Reference and Input
               N   X  INCX
               |   |   |
SUMM = SCASUM( 5 , X , 1  )
 
X        =  ((1.0, 2.0), (-3.0, 4.0), (5.0, -6.0 ), (-7.0, -8.0),
             (9.0, 10.0))

Output
SUMM     =  55.0

[ Top of Page | Previous Page | Next Page | Table of Contents | Index ]