Engineering and Scientific Subroutine Library for AIX Version 3 Release 3: Guide and Reference

SNRM2, DNRM2, SCNRM2, and DZNRM2--Euclidean Length of a Vector with Scaling of Input to Avoid Destructive Underflow and Overflow

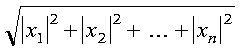
These subprograms compute the Euclidean length (l₂ norm) of vector x, with scaling of input to avoid destructive underflow and overflow.

Table 46. Data Types

Note:

If there is a possibility that your data will cause the computation to overflow or underflow, you should use these subroutines instead of SNORM2, DNORM2, CNORM2, and ZNORM2, because the intermediate computational results may exceed the maximum or minimum limits of the machine. Notes explains how to estimate whether your data will cause an overflow or underflow.

Syntax

On Entry

n

is the number of elements in vector x. Specified as: a fullword integer; n >= 0.

x

is the vector x of length n, whose Euclidean length is to be computed. Specified as: a one-dimensional array of (at least) length 1+(n-1)|incx|, containing numbers of the data type indicated in Table 46.

incx

is the stride for vector x. Specified as: a fullword integer. It can have any value.

On Return

Function value

is the Euclidean length (l₂ norm) of the vector x. Returned as: a number of the data type indicated in Table 46.

Note

Declare this function in your program as returning a value of the data type indicated in Table 46.

Function

The Euclidean length (l₂ norm) of vector x is expressed as follows, with scaling of input to avoid destructive underflow and overflow:

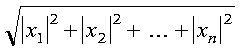
See reference [79]. The result is returned as the function value. If n is 0, then 0.0 is returned as the value of the function.

For SNRM2 and SCNRM2, the sum of the squares of the absolute values of the elements is accumulated in long precision. The square root of this long-precision sum is then computed and, if necessary, is unscaled.

Although these subroutines eliminate destructive underflow, nondestructive underflows may occur if the input elements differ greatly in magnitude. This does not affect accuracy, but it degrades performance. The system default is to mask underflow, which improves the performance of these subroutines.

Error Conditions

Computational Errors

None

Input-Argument Errors

n < 0

Important Information About the Following Examples

Workstations use workstation architecture precisions: ANSI/IEEE 32-bit and 64-bit binary floating-point format. The ranges are:

• For short-precision: 3.37×10^-38 to 3.37×10³⁸
• For long-precision: 1.67×10^-308 to 1.67×10³⁰⁸

Example 1

This example shows a vector, x, whose elements must be scaled to prevent overflow.

Function Reference and Input

               N   X  INCX
               |   |   |
DNORM = DNRM2( 6 , X , 1  )
 
X      = (0.68056D+200, 0.25521D+200, 0.34028D+200,
          0.85071D+200, 0.25521D+200, 0.85071D+200)

Output

DNORM    =  0.1469D+201

Example 2

This example shows a vector, x, whose elements must be scaled to prevent destructive underflow.

Function Reference and Input

               N   X  INCX
               |   |   |
DNORM = DNRM2( 4 , X , 2  )
 
X     = (0.10795D-200, . , 0.10795D-200, . , 0.10795D-200,
         . , 0.10795D-200)

Output

DNORM    =  0.21590D-200

Example 3

This example shows a vector, x, with a stride of 0. The result in SNORM is:

Function Reference and Input

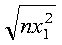
               N   X  INCX
               |   |   |
SNORM = SNRM2( 4 , X , 0  )
 
X        =  (4.0)

Output

SNORM    =  8.0

Example 4

This example shows a vector, x, containing complex numbers, and whose elements must be scaled to prevent overflow.

Function Reference and Input

                 N   X  INCX
                 |   |   |
DZNORM = DZNRM2( 3 , X , 1  )
 
X     = ((0.68056D+200, 0.25521D+200), (0.34028D+200, 0.85071D+200),
         (0.25521D+200, 0.85071D+200))

Output

DZNORM   =  0.1469D+201

Example 5

This example shows a vector, x, containing complex numbers, and whose elements must be scaled to prevent destructive underflow.

Function Reference and Input

                 N   X  INCX
                 |   |   |
DZNORM = DZNRM2( 2 , X , 2  )
 
X     = ((0.10795D-200, 0.10795D-200), . ,
         (0.10795D-200, 0.10795D-200))

Output

DZNORM   =  0.2159D-200