Engineering and Scientific Subroutine Library for AIX Version 3 Release 3: Guide and Reference

SNORM2, DNORM2, CNORM2, and ZNORM2--Euclidean Length of a Vector with No Scaling of Input

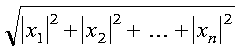
These subprograms compute the euclidean length (l₂ norm) of vector x with no scaling of input.

Table 47. Data Types

Syntax

On Entry

n

is the number of elements in vector x. Specified as: a fullword integer; n >= 0.

x

is the vector x of length n, whose euclidean length is to be computed. Specified as: a one-dimensional array of (at least) length 1+(n-1)|incx|, containing numbers of the data type indicated in Table 47.

incx

is the stride for vector x. Specified as: a fullword integer. It can have any value.

On Return

Function value

is the euclidean length (l₂ norm) of the vector x. Returned as: a number of the data type indicated in Table 47.

Notes

1. This subroutine does not underflow or overflow if the values of the elements in vector x conform to the following conditions. If these conditions are violated, overflow or destructive underflow may occur:
   • For short-precision numbers:

     Any valid short-precision number.

   • For long-precision numbers:

     |x_i| = 0 or 0.10010E-145 < |x_i| < 0.13408E+155 for i = 1, n

2. Declare this function in your program as returning a value of the data type indicated in Table 47.

Function

The euclidean length (l₂ norm) of vector x is expressed as follows with no scaling of input:

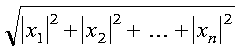
See reference [79]. The result is returned as the function value. If n is 0, then 0.0 is returned as the value of the function.

For SNORM2 and CNORM2, the sum of the squares of the absolute values of the elements is accumulated in long-precision. The square root of this long-precision sum is then computed.

This subroutine should not be used if the values in vector x do not conform to the restriction given in Notes.

Error Conditions

Computational Errors

None

Input-Argument Errors

n < 0

Example 1

This example shows a vector, x, with a stride of 1.

Function Reference and Input

                N   X  INCX
                |   |   |
SNORM = SNORM2( 6 , X , 1  )
 
X        =  (3.0, 4.0, 1.0, 8.0, 1.0, 3.0)

Output

SNORM    =  10.0

Example 2

This example shows a vector, x, with a stride greater than 1.

Function Reference and Input

                N   X  INCX
                |   |   |
SNORM = SNORM2( 6 , X , 2  )
 
X        =  (3.0, . , 4.0, . , 1.0, . , 8.0, . , 1.0, . , 3.0)

Output

SNORM    =  10.0

Example 3

This example shows a vector, x, with a stride of 0. The result in SNORM is:

Function Reference and Input

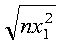
                N   X  INCX
                |   |   |
SNORM = SNORM2( 4 , X , 0  )
 
X        =  (4.0)

Output

SNORM    =  8.0

Example 4

This example shows a vector, x, containing complex numbers and having a stride of 1.

Function Reference and Input

                N   X  INCX
                |   |   |
CNORM = CNORM2( 3 , X , 1  )
 
X        =  ((3.0, 4.0), (1.0, 8.0), (-1.0, 3.0))

Output

CNORM    =  10.0