Engineering and Scientific Subroutine Library for AIX Version 3 Release 3: Guide and Reference

SVEA, DVEA, CVEA, and ZVEA--Add a Vector X to a Vector Y and Store in a Vector Z

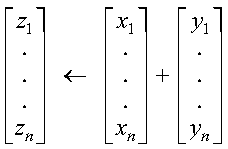
These subprograms perform the following computation, using vectors x, y, and z:

z<--x+y

Table 52. Data Types

Syntax

On Entry

n

is the number of elements in vectors x, y, and z. Specified as: a fullword integer; n >= 0.

x

is the vector x of length n. Specified as: a one-dimensional array of (at least) length 1+(n-1)|incx|, containing numbers of the data type indicated in Table 52.

incx

is the stride for vector x. Specified as: a fullword integer. It can have any value.

y

is the vector y of length n. Specified as: a one-dimensional array of (at least) length 1+(n-1)|incy|, containing numbers of the data type indicated in Table 52.

incy

is the stride for vector y. Specified as: a fullword integer. It can have any value.

z

See On Return.

incz

is the stride for vector z. Specified as: a fullword integer. It can have any value.

On Return

z

is the vector z of length n, containing the result of the computation. Returned as: a one-dimensional array of (at least) length 1+(n-1)|incz|, containing numbers of the data type indicated in Table 52.

Notes

1. If you specify the same vector for x and z, then incx and incz must be equal; otherwise, results are unpredictable. The same is true for y and z.
2. If you specify different vectors for x and z, they must have no common elements; otherwise, results are unpredictable. The same is true for y and z. See Concepts.

Function

The computation is expressed as follows:

If n is 0, no computation is performed.

Error Conditions

Computational Errors

None

Input-Argument Errors

n < 0

Example 1

This example shows vectors x, y, and z, with positive strides.

Call Statement and Input

           N   X  INCX  Y  INCY  Z  INCZ
           |   |   |    |   |    |   |
CALL SVEA( 5 , X , 1  , Y , 2  , Z , 1  )
 
X        =  (1.0, 2.0, 3.0, 4.0, 5.0)
Y        =  (1.0, . , 1.0, . , 1.0, . , 1.0, . , 1.0)

Output

Z        =  (2.0, 3.0, 4.0, 5.0, 6.0)

Example 2

This example shows vectors x and y having strides of opposite sign, and an output vector z having a positive stride. For y, which has negative stride, processing begins at element Y(5), which is 1.0.

Call Statement and Input

           N   X  INCX  Y   INCY  Z  INCZ
           |   |   |    |    |    |   |
CALL SVEA( 5 , X , 1  , Y , -1  , Z , 2  )
 
X        =  (1.0, 2.0, 3.0, 4.0, 5.0)
Y        =  (5.0, 4.0, 3.0, 2.0, 1.0)

Output

Z        =  (2.0, . , 4.0, . , 6.0, . , 8.0, . , 10.0)

Example 3

This example shows a vector, x, with 0 stride and a vector, z, with negative stride. x is treated like a vector of length n, all of whose elements are the same as the single element in x. For vector z, results are stored beginning in element Z(5).

Call Statement and Input

           N   X  INCX  Y  INCY  Z   INCZ
           |   |   |    |   |    |    |
CALL SVEA( 5 , X , 0  , Y , 1  , Z , -1  )
 
X        =  (1.0)
Y        =  (5.0, 4.0, 3.0, 2.0, 1.0)

Output

Z        =  (2.0, 3.0, 4.0, 5.0, 6.0)

Example 4

This example shows a vector, y, with 0 stride. y is treated like a vector of length n, all of whose elements are the same as the single element in y.

Call Statement and Input

           N   X  INCX  Y  INCY  Z  INCZ
           |   |   |    |   |    |   |
CALL SVEA( 5 , X , 1  , Y , 0  , Z , 1  )
 
X        =  (1.0, 2.0, 3.0, 4.0, 5.0)
Y        =  (5.0)

Output

Z        =  (6.0, 7.0, 8.0, 9.0, 10.0)

Example 5

This example shows the output vector, z, with 0 stride, where the vector x has positive stride, and the vector y has 0 stride. The number of elements to be processed, n, is greater than 1.

Call Statement and Input

           N   X  INCX  Y  INCY  Z  INCZ
           |   |   |    |   |    |   |
CALL SVEA( 5 , X , 1  , Y , 0  , Z , 0  )
 
X        =  (1.0, 2.0, 3.0, 4.0, 5.0)
Y        =  (5.0)

Output

Z        =  (10.0)

Example 6

This example shows the output vector z, with 0 stride, where the vector x has 0 stride, and the vector y has negative stride. The number of elements to be processed, n, is greater than 1.

Call Statement and Input

           N   X  INCX  Y   INCY  Z  INCZ
           |   |   |    |    |    |   |
CALL SVEA( 5 , X , 0  , Y , -1  , Z , 0  )
 
X        =  (1.0)
Y        =  (5.0, 4.0, 3.0, 2.0, 1.0)

Output

Z        =  (6.0)

Example 7

This example shows how SVEA can be used to compute a scalar value. In this case, vectors x and y contain scalar values. The strides of all vectors, x, y, and z, are 0. The number of elements to be processed, n, is 1.

Call Statement and Input

           N   X  INCX  Y  INCY  Z  INCZ
           |   |   |    |   |    |   |
CALL SVEA( 1 , X , 0  , Y , 0  , Z , 0  )
 
X        =  (1.0)
Y        =  (5.0)

Output

Z        =  (6.0)

Example 8

This example shows vectors x and y, containing complex numbers and having positive strides.

Call Statement and Input

           N   X  INCX  Y  INCY  Z  INCZ
           |   |   |    |   |    |   |
CALL CVEA( 3 , X , 1  , Y , 2  , Z , 1  )
 
X        =  ((1.0, 2.0), (3.0, 4.0), (5.0, 6.0))
Y        =  ((7.0, 8.0), . , (9.0, 10.0), . , (11.0, 12.0))

Output

Z        =  ((8.0, 10.0), (12.0, 14.0), (16.0, 18.0))