Engineering and Scientific Subroutine Library for AIX Version 3 Release 3: Guide and Reference

SSWAP, DSWAP, CSWAP, and ZSWAP--Interchange the Elements of Two Vectors

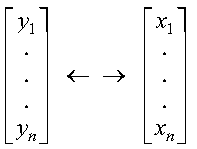
These subprograms interchange the elements of vectors x and y:

y <--> x

Table 51. Data Types

Syntax

On Entry

n

is the number of elements in vectors x and y. Specified as: a fullword integer; n >= 0.

x

is the vector x of length n. Specified as: a one-dimensional array of (at least) length 1+(n-1)|incx|, containing numbers of the data type indicated in Table 51.

incx

is the stride for vector x. Specified as: a fullword integer. It can have any value.

y

is the vector y of length n. Specified as: a one-dimensional array of (at least) length 1+(n-1)|incy|, containing numbers of the data type indicated in Table 51.

incy

is the stride for vector y. Specified as: a fullword integer. It can have any value.

On Return

x

is the vector x of length n, containing the elements that were swapped from vector y. Returned as: a one-dimensional array, containing numbers of the data type indicated in Table 51.

y

is the vector y of length n, containing the elements that were swapped from vector x. Returned as: a one-dimensional array, containing numbers of the data type indicated in Table 51.

Notes

1. If you specify the same vector for x and y, then incx and incy must be equal; otherwise, results are unpredictable.
2. If you specify different vectors for x and y, they must have no common elements; otherwise, results are unpredictable. See Concepts.

Function

The elements of vectors x and y are interchanged as follows:

See reference [79]. If n is 0, no elements are interchanged.

Error Conditions

Computational Errors

None

Input-Argument Errors

n < 0

Example 1

This example shows vectors x and y with positive strides.

Call Statement and Input

            N   X  INCX  Y  INCY
            |   |   |    |   |
CALL SSWAP( 5 , X , 1  , Y , 2  )
 
X        =  (1.0, 2.0, 3.0, 4.0, 5.0)
Y        =  (-1.0, . , -2.0, . , -3.0, . , -4.0, . , -5.0)

Output

X        =  (-1.0, -2.0, -3.0, -4.0, -5.0)
Y        =  (1.0, . , 2.0, . , 3.0, . , 4.0, . , 5.0)

Example 2

This example shows how to obtain output vectors x and y that are reverse copies of the input vectors y and x. You must specify strides with the same absolute value, but with opposite signs. For y, which has negative stride, processing begins at element Y(5), which is -5.0, and the results of the swap are stored beginning at the same element.

Call Statement and Input

            N   X  INCX  Y   INCY
            |   |   |    |    |
CALL SSWAP( 5 , X , 1  , Y , -1  )
 
X        =  (1.0, 2.0, 3.0, 4.0, 5.0)
Y        =  (-1.0, -2.0, -3.0, -4.0, -5.0)

Output

X        =  (-5.0, -4.0, -3.0, -2.0, -1.0)
Y        =  (5.0, 4.0, 3.0, 2.0, 1.0)

Example 3

This example shows how SSWAP can be used to interchange scalar values in vectors x and y by specifying 0 strides and the number of elements to be processed as 1.

Call Statement and Input

            N   X  INCX  Y  INCY
            |   |   |    |   |
CALL SSWAP( 1 , X , 0  , Y , 0  )
 
X        =  (1.0)
Y        =  (-4.0)

Output

X        =  (-4.0)
Y        =  (1.0)

Example 4

This example shows vectors x and y, containing complex numbers and having positive strides.

Call Statement and Input

            N   X  INCX  Y  INCY
            |   |   |    |   |
CALL CSWAP( 4 , X , 1  , Y , 2  )
 
X        =  ((1.0, 6.0), (2.0, 7.0), (3.0, 8.0), (4.0, 9.0))
Y        =  ((-1.0, -1.0), . , (-2.0, -2.0), . , (-3.0, -3.0), . ,
             (-4.0, -4.0))

Output

X        =  ((-1.0, -1.0), (-2.0, -2.0), (-3.0, -3.0), (-4.0, -4.0))
Y        =  ((1.0, 6.0), . , (2.0, 7.0), . , (3.0, 8.0), . ,
             (4.0, 9.0))