Parallel Engineering and Scientific Subroutine Library for AIX Version 2 Release 3: Guide and Reference
This subroutine solves the following system of equations for multiple
right-hand sides:
- AX = B
where, in the formula above:
- A represents the global positive definite symmetric band
submatrix Aja:ja+n-1,
ja:ja+n-1 to be factored by
Cholesky factorization.
- B represents the global general submatrix
Bib:ib+n-1,
1:nrhs containing the right-hand sides in its
columns.
- X represents the global general submatrix
Bib:ib+n-1,
1:nrhs containing the output solution vectors in its
columns.
If n = 0, no computation is performed and the subroutine
returns after doing some parameter checking. See references [2], [23], [39], and [40].
Table 68. Data Types
| A, B, work
| Subroutine
|
| Long-precision real
| PDPBSV
|
| Fortran
| CALL PDPBSV (uplo, n, k, nrhs,
a, ja, desc_a, b, ib,
desc_b, work, lwork, info)
|
| C and C++
| pdpbsv (uplo, n, k, nrhs, a,
ja, desc_a, b, ib, desc_b,
work, lwork, info);
|
- uplo
- indicates whether the upper or lower triangular part of the global
submatrix A is referenced, where:
If uplo = 'U', the upper triangular part is
referenced.
If uplo = 'L', the lower triangular part is
referenced.
Scope: global
Specified as: a single character;
uplo = 'U' or 'L'.
- n
- is the number of columns in the submatrix A, stored in the
upper- or lower-band-packed storage mode. It is also the number of rows
in the general submatrix B containing the multiple right-hand
sides.
Scope: global
Specified as: a fullword integer;
0 <= n <= (NB_A)p-mod(ja-1,NB_A).
- k
- is the half bandwidth of the submatrix A.
Scope: global
Specified as: a fullword integer, where:
- If uplo = 'U',
0 <= k <= NB_A.
- If uplo = 'L',
0 <= k < n.
These limits for k are extensions of the ScaLAPACK
standard.
- nrhs
- is the number of columns in submatrix B used in the
computation.
Scope: global
Specified as: a fullword integer;
nrhs >= 0.
- a
- is the local part of the global positive definite symmetric band matrix
A, stored in upper- or lower-band-packed storage mode, to be
factored. This identifies the first element of the local
array A. This subroutine computes the location of the first
element of the local subarray used, based on k, ja,
desc_a, and p; therefore, the leading k+1 by
LOCp(ja+n-1) part of the local array A must
contain the local pieces of the leading k+1 by
ja+n-1 part of the global matrix, and:
- If uplo = 'U', the leading
n × n upper triangular part of the global
submatrix Aja:ja+n-1,
ja:ja+n-1 must contain the upper
triangular part of the submatrix, and the strictly lower triangular part is
not referenced.
- If uplo = 'L', the leading
n × n lower triangular part of the global
submatrix Aja:ja+n-1,
ja:ja+n-1 must contain the lower
triangular part of the submatrix, and the strictly upper triangular part is
not referenced.
Scope: local
Specified as: an LLD_A by (at least)
LOCp(ja+n-1) array, containing numbers of the data
type indicated in Table 68. Details about the block-cyclic data distribution of
global matrix A are stored in desc_a.
On output, array A is overwritten; that is, original input
is not preserved.
- ja
- is the column index of the global matrix A, identifying the
first column of the submatrix A.
Scope: global
Specified as: a fullword integer;
1 <= ja <= N_A and
ja+n-1 <= N_A.
- desc_a
- is the array descriptor for global matrix A, which may be type
501 or type 1, as described in the following tables. For rules on using
array descriptors, see Notes and Coding Rules.
| desc_a
| Name
| Description
| Limits
| Scope
|
| 1
| DTYPE_A
| Descriptor Type
| DTYPE_A = 501 for 1 × p or
p × 1
where p is the number of processes in a process grid.
| Global
|
| 2
| CTXT_A
| BLACS context
| Valid value, as returned by BLACS_GRIDINIT or BLACS_GRIDMAP
| Global
|
| 3
| N_A
| Number of columns in the global matrix
|
If n = 0:
N_A >= 0
Otherwise:
N_A >= 1
| Global
|
| 4
| NB_A
| Column block size
| NB_A >= 1 and
0 <= n <= (NB_A)p-mod(ja-1,NB_A)
| Global
|
| 5
| CSRC_A
| The process column over which the first column of the global matrix is
distributed
| 0 <= CSRC_A < p
| Global
|
| 6
| LLD_A
| Leading dimension
| LLD_A >= k+1
| Local
|
| 7
| --
| Reserved
| --
| --
|
Specified as: an array of (at least) length 7, containing fullword
integers.
| desc_a
| Name
| Description
| Limits
| Scope
|
| 1
| DTYPE_A
| Descriptor type
| DTYPE_A = 1 for 1 × p
where p is the number of processes in a process grid.
| Global
|
| 2
| CTXT_A
| BLACS context
| Valid value, as returned by BLACS_GRIDINIT or BLACS_GRIDMAP
| Global
|
| 3
| M_A
| Number of rows in the global matrix
| M_A > k
| Global
|
| 4
| N_A
| Number of columns in the global matrix
|
If n = 0:
N_A >= 0
Otherwise:
N_A >= 1
| Global
|
| 5
| MB_A
| Row block size
| MB_A >= 1
| Global
|
| 6
| NB_A
| Column block size
| NB_A >= 1 and
0 <= n <= (NB_A)p-mod(ja-1,NB_A)
| Global
|
| 7
| RSRC_A
| The process row over which the first row of the global matrix is
distributed
| RSRC_A=0
| Global
|
| 8
| CSRC_A
| The process column over which the first column of the global matrix is
distributed
| 0 <= CSRC_A < p
| Global
|
| 9
| LLD_A
| The leading dimension of the local array
| LLD_A >= k+1
| Local
|
Specified as: an array of (at least) length 9, containing fullword
integers.
- b
- is the local part of the global general matrix B, containing
the multiple right-hand sides of the system. This identifies the
first element of the local array B. This
subroutine computes the location of the first element of the local subarray
used, based on ib, desc_b, and p; therefore,
the leading LOCp(ib+n-1) by nrhs part of the
local array B must contain the local pieces of the leading
ib+n-1 by nrhs part of the global
matrix.
Scope: local
Specified as: an LLD_B by (at least) nrhs array, containing
numbers of the data type indicated in Table 68. Details about the block-cyclic data distribution of
global matrix B are stored in desc_b.
- ib
- is the row index of the global matrix B, identifying the first
row of the submatrix B.
Scope: global
Specified as: a fullword integer;
1 <= ib <= M_B and
ib+n-1 <= M_B.
- desc_b
- is the array descriptor for global matrix B, which may be type
502 or type 1, as described in the following tables. For rules on using
array descriptors, see Notes and Coding Rules.
| desc_b
| Name
| Description
| Limits
| Scope
|
| 1
| DTYPE_B
| Descriptor type
| DTYPE_B = 502 for p × 1 or
1 × p
where p is the number of processes in a process grid.
| Global
|
| 2
| CTXT_B
| BLACS context
| Valid value, as returned by BLACS_GRIDINIT or BLACS_GRIDMAP
| Global
|
| 3
| M_B
| Number of rows in the global matrix
|
If n = 0:
M_B >= 0
Otherwise:
M_B >= 1
| Global
|
| 4
| MB_B
| Row block size
| MB_B >= 1 and
0 <= n <= (MB_B)p-mod(ib-1,MB_B)
| Global
|
| 5
| RSRC_B
| The process row over which the first row of the global matrix is
distributed
| 0 <= RSRC_B < p
| Global
|
| 6
| LLD_B
| Leading dimension
| LLD_B >= max(1,LOCp(M_B))
| Local
|
| 7
| --
| Reserved
| --
| --
|
Specified as: an array of (at least) length 7, containing fullword
integers.
| desc_b
| Name
| Description
| Limits
| Scope
|
| 1
| DTYPE_B
| Descriptor type
| DTYPE_B = 1 for p × 1
where p is the number of processes in a process grid.
| Global
|
| 2
| CTXT_B
| BLACS context
| Valid value, as returned by BLACS_GRIDINIT or BLACS_GRIDMAP
| Global
|
| 3
| M_B
| Number of rows in the global matrix
|
If n = 0:
M_B >= 0
Otherwise:
M_B >= 1
| Global
|
| 4
| N_B
| Number of columns in the global matrix
| N_B >= nrhs
| Global
|
| 5
| MB_B
| Row block size
| MB_B >= 1 and
0 <= n <= (MB_B)p-mod(ib-1,MB_B)
| Global
|
| 6
| NB_B
| Column block size
| NB_B >= 1
| Global
|
| 7
| RSRC_B
| The process row over which the first row of the global matrix is
distributed
| 0 <= RSRC_B < p
| Global
|
| 8
| CSRC_B
| The process column over which the first column of the global matrix is
distributed
| CSRC_B=0
| Global
|
| 9
| LLD_B
| Leading dimension
| LLD_B >= max(1,LOCp(M_B)
| Local
|
Specified as: an array of (at least) length 9, containing fullword
integers.
- work
- has the following meaning:
If lwork = 0, work is ignored.
If lwork <> 0, work is the work area used by
this subroutine, where:
- If lwork <> -1, the size of work is (at least)
of length lwork.
- If lwork = -1, the size of work is (at least) of
length 1.
Scope: local
Specified as: an area of storage containing numbers of data type
indicated in Table 68.
- lwork
- is the number of elements in array WORK.
Scope:
- If lwork >= 0, lwork is local
- If lwork = -1, lwork is global
Specified as: a fullword integer, where:
- info
- See On Return.
- a
- a is overwritten; that is, the original input is not
preserved. This subroutine overwrites data in positions that do not
contain the positive definite symmetric band matrix A stored in
upper- or lower-band-packed storage mode.
- b
- b is the updated local part of the global matrix B,
containing the solution vectors.
Scope: local
Returned as: an LLD_B by (at least) nrhs array, containing
numbers of the data type indicated in Table 68.
- work
- is the work area used by this subroutine if lwork <> 0,
where:
If lwork <> 0 and lwork <> -1, the
size of work is (at least) of length lwork.
If lwork = -1, the size of work is (at least) of
length 1.
Scope: local
Returned as: an area of storage, containing numbers of the data type
indicated in Table 68, where:
- If lwork >= 1, work1 is set to the
minimum lwork value needed.
- If lwork = -1, work1 is set to the
optimum lwork value needed.
Except for work1, the contents of work are
overwritten on return.
- info
- has the following meaning:
If info = 0, global submatrix A is positive
definite, and the factorization completed normally or the work area query
completed successfully.
If info > 0, the leading minor of order i of
the global submatrix A is not positive definite.
info is set equal to i, where the first leading minor was
encountered at Aja+i-1,
ja+i-1. The results contained in matrix
A are not defined.
Scope: global
Returned as: a fullword integer;
info >= 0.
- In your C program, argument info must be passed by
reference.
- If n > 0 and nrhs = 0, only the
factorization is completed.
- The subroutine accepts lowercase letters for the uplo
argument.
- This subroutine gives the best performance for wide band widths, for
example:
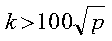
where p is the number of processes. For details, see
references [2], [39], and [40].
Also, it is suggested that you specify
uplo = 'L'.
- A, B, and work must have no common
elements; otherwise, results are unpredictable.
- In all cases, follow these rules:
- ib = ja
- DTYPE_A=501 or 1
- DTYPE_B=502 or 1
- NB_A = MB_B
- If DTYPE_A=1, RSRC_A=0, M_A >= k+1, and MB_A >= 1.
- If DTYPE_B=1, CSRC_B=0, N_B >= nrhs, and NB_B >= 1.
- CTXT_A = CTXT_B
- Following are the consistent combinations of array descriptor types and
process grids, where p is the number of processes in the process
grid:
| DTYPE_A
| DTYPE_B
| Process Grid
|
| 501
| 502
| p × 1 or 1 × p
|
| 501
| 1
| 1 × p
|
| 1
| 502
| p × 1
|
| 1
| 1
| 1 × 1
|
- To determine the values of LOCp(n) used in the argument
descriptions, see Determining the Number of Rows and Columns in Your Local Arrays for descriptor type-1 or Determining the Number of Rows or Columns in Your Local Arrays for descriptor type-501 and
type-502.
- The global band matrix A must be positive definite. If
A is not positive definite, this subroutine uses the info
argument to provide information about A and issues an error
message. This differs from ScaLAPACK, which only uses the info
argument to provide information about A.
- The global positive definite symmetric band matrix A must be
stored in upper- or lower-band-packed storage mode. See the section on
block-cyclically distributing a symmetric matrix in Matrices.
Matrix A must be distributed over a one-dimensional process grid
using block-cyclic data distribution. For more information on using
block-cyclic data distribution, see Specifying Block-Cyclically-Distributed Matrices for the Banded Linear Algebraic Equations.
- Matrix B must be distributed over a one-dimensional process
grid, using block-cyclic data distribution. For more information on
block-cyclic data distribution, see Specifying Block-Cyclically-Distributed Matrices for the Banded Linear Algebraic Equations. Also, see the section on distributing the right-hand
side matrix in Matrices.
- If lwork = -1 on any process, it must equal
-1 on all processes. That is, if a subset of the processes
specifies -1 for the work area size, they must all specify
-1.
- Although global matrices A and B may be
block-cyclically distributed on a 1 × p or
p × 1 process grid, the values of n,
ja, ib, NB_A and MB_B, must be chosen so that each process
has at most one full or partial block of each of the global submatrices
A and B.
Matrix A is not positive definite (corresponding computational
error messages are issued by both PDPBTRF and PDPBSV). For details, see
the description of the info argument.
lwork = 0 and unable to allocate workspace
Stage 1:
- DTYPE_A is invalid.
- DTYPE_B is invalid.
Stage 2:
- CTXT_A is invalid.
Stage 3:
- PDPBSV was called from outside the process grid.
Stage 4:
- The process grid is not 1 × p or
p × 1.
- uplo <> 'U' or 'L'
- n < 0
- k < 0
- k+1 > n
- ja < 1
- DTYPE_A = 1 and:
- M_A < k+1
- MB_A < 1
- RSRC_A <> 0
- The process grid is not 1 × p.
- N_A < 0 and (n = 0); N_A < 1
otherwise
- NB_A < 1
- n+mod(ja-1, NB_A) > (NB_A)p
- CSRC_A < 0 or CSRC_A >= p
- uplo = 'U' and k > NB_A
- nrhs < 0
- ib <> ja
- ib < 1
- DTYPE_B = 1 and:
- N_B < nrhs
- NB_B < 1
- CSRC_B <> 0
- The process grid is not p × 1.
- M_B < 0 and (n = 0); M_B < 1
otherwise
- MB_B < 1
- n+mod(ib-1,MB_B) > (MB_B)p
- MB_B <> NB_A
- RSRC_B < 0 or RSRC_B >= p
- CTXT_A <> CTXT_B
Stage 5:
If n <> 0:
- ja+n-1 > N_A
- ja > N_A
- ib > M_B
- ib+n-1 > M_B
- LLD_A < k+1
Stage 6:
- LLD_B < max(1, LOCp(M_B))
- lwork <> 0, lwork <> -1, and
lwork < (NB_A+2k)(k)+max(nrhs,
k)(k)
Stage 7:
Each of the following global input arguments are checked to determine
whether its value differs from the value specified on process
P00:
- uplo differs.
- n differs.
- k differs.
- nrhs differs.
- ja differs.
- DTYPE_A differs.
- DTYPE_A does not differ and:
- N_A differs.
- NB_A differs.
- CSRC_A differs.
- DTYPE_A = 1 and:
- M_A differs.
- MB_A differs.
- RSRC_A differs.
- ib differs.
- DTYPE_B differs.
- DTYPE_B does not differ and:
- M_B differs.
- MB_B differs.
- RSRC_B differs.
- DTYPE_A = 1 and:
- N_B differs.
- NB_B differs.
- CSRC_B differs.
Also:
- lwork = -1 on a subset of processes.
This example shows a factorization of the positive definite symmetric band
matrix A of order 9 with a half bandwidth of 7:
* *
| 1.0 1.0 1.0 1.0 1.0 1.0 1.0 1.0 0.0 |
| 1.0 2.0 2.0 2.0 2.0 2.0 2.0 2.0 1.0 |
| 1.0 2.0 3.0 3.0 3.0 3.0 3.0 3.0 2.0 |
| 1.0 2.0 3.0 4.0 4.0 4.0 4.0 4.0 3.0 |
| 1.0 2.0 3.0 4.0 5.0 5.0 5.0 5.0 4.0 |
| 1.0 2.0 3.0 4.0 5.0 6.0 6.0 6.0 5.0 |
| 1.0 2.0 3.0 4.0 5.0 6.0 7.0 7.0 6.0 |
| 1.0 2.0 3.0 4.0 5.0 6.0 7.0 8.0 7.0 |
| 0.0 1.0 2.0 3.0 4.0 5.0 6.0 7.0 8.0 |
* *
Matrix A is stored in lower-band-packed storage mode:
* *
| 1.0 2.0 3.0 4.0 5.0 6.0 7.0 8.0 8.0 |
| 1.0 2.0 3.0 4.0 5.0 6.0 7.0 7.0 . |
| 1.0 2.0 3.0 4.0 5.0 6.0 6.0 . . |
| 1.0 2.0 3.0 4.0 5.0 5.0 . . . |
| 1.0 2.0 3.0 4.0 4.0 . . . . |
| 1.0 2.0 3.0 3.0 . . . . . |
| 1.0 2.0 2.0 . . . . . . |
| 1.0 1.0 . . . . . . . |
* *
where "." means you do not have to store a value in that
position in the local array. However, these storage positions are
required and are overwritten during the computation.
Notes:
- On output, the submatrix A is overwritten; that is, the
original input is not preserved.
- Notice only one process grid was created, even though,
DTYPE_A = 501 and DTYPE_B = 502.
- Because lwork = 0, PDPBSV dynamically allocates the work
area used by this subroutine.
ORDER = 'R'
NPROW = 1
NPCOL = 3
CALL BLACS_GET (0, 0, ICONTXT)
CALL BLACS_GRIDINIT(ICONTXT, ORDER, NPROW, NPCOL)
CALL BLACS_GRIDINFO(ICONTXT, NPROW, NPCOL, MYROW, MYCOL)
UPLO N K NRHS A JA DESC_A B IB DESC_B WORK LWORK INFO
| | | | | | | | | | | | |
CALL PDPBSV( 'L' , 9 , 7 , 3 , A , 1 , DESC_A , B , 1 , DESC_B , WORK , 0 , INFO )
| Desc_A
|
| DTYPE_
| 501
|
| CTXT_
| icontxt(CGBTOO7)
|
| N_
| 9
|
| NB_
| 3
|
| CSRC_
| 0
|
| LLD_A
| 8
|
| Reserved
| --
|
|
Notes:
- icontxt is the output of the BLACS_GRIDINIT
call.
|
| Desc_B
|
| DTYPE_
| 502
|
| CTXT_
| icontxt(CGBTOO8)
|
| M_
| 9
|
| MB_
| 3
|
| RSRC_
| 0
|
| LLD_B
| 3
|
| Reserved
| --
|
|
Notes:
- icontxt is the output of the BLACS_GRIDINIT
call.
|
Global matrix A stored in lower-band-packed storage mode with
block size of 3:
B,D 0 1 2
* *
| 1.0 2.0 3.0 | 4.0 5.0 6.0 | 7.0 8.0 8.0 |
| 1.0 2.0 3.0 | 4.0 5.0 6.0 | 7.0 7.0 . |
| 1.0 2.0 3.0 | 4.0 5.0 6.0 | 6.0 . . |
| 1.0 2.0 3.0 | 4.0 5.0 5.0 | . . . |
0 | 1.0 2.0 3.0 | 4.0 4.0 . | . . . |
| 1.0 2.0 3.0 | 3.0 . . | . . . |
| 1.0 2.0 2.0 | . . . | . . . |
| 1.0 1.0 . | . . . | . . . |
* *
The following is the 1 × 3 process grid:
B,D | 0 | 1 | 2
-----| ------- | ------- |-------
0 | P00 | P01 | P02
Local array A with block size of 3:
p,q | 0 | 1 | 2
-----|-----------------|------------------|-----------------
| 1.0 2.0 3.0 | 4.0 5.0 6.0 | 7.0 8.0 8.0
| 1.0 2.0 3.0 | 4.0 5.0 6.0 | 7.0 7.0 .
| 1.0 2.0 3.0 | 4.0 5.0 6.0 | 6.0 . .
| 1.0 2.0 3.0 | 4.0 5.0 5.0 | . . .
0 | 1.0 2.0 3.0 | 4.0 4.0 . | . . .
| 1.0 2.0 3.0 | 3.0 . . | . . .
| 1.0 2.0 2.0 | . . . | . . .
| 1.0 1.0 . | . . . | . . .
Global matrix B with block size of 3:
B,D 0
* *
| 8.0 36.0 44.0 |
0 | 16.0 80.0 80.0 |
| 23.0 122.0 108.0 |
| ----------------- |
| 29.0 161.0 129.0 |
1 | 34.0 196.0 144.0 |
| 38.0 226.0 154.0 |
| ----------------- |
| 41.0 250.0 160.0 |
2 | 43.0 267.0 163.0 |
| 36.0 240.0 120.0 |
* *
The following is the 1 × 3 process grid:
B,D | 0 | 1 | 2
-----| ------- | ------- |-------
0 | P00 | P01 | P02
Local array B with block size of 3:
p,q | 0 | 1 | 2
-----|--------------------|---------------------|--------------------
| 8.0 36.0 44.0 | 29.0 161.0 129.0 | 41.0 250.0 160.0
0 | 16.0 80.0 80.0 | 34.0 196.0 144.0 | 43.0 267.0 163.0
| 23.0 122.0 108.0 | 38.0 226.0 154.0 | 36.0 240.0 120.0
Output:
Global matrix B with block size of 3:
B,D 0
* *
| 1.0 1.0 9.0 |
0 | 1.0 2.0 8.0 |
| 1.0 3.0 7.0 |
| -------------- |
| 1.0 4.0 6.0 |
1 | 1.0 5.0 5.0 |
| 1.0 6.0 4.0 |
| -------------- |
| 1.0 7.0 3.0 |
2 | 1.0 8.0 2.0 |
| 1.0 9.0 1.0 |
* *
The following is the 1 × 3 process grid:
B,D | 0 | 1 | 2
-----| ------- | ------- |-------
0 | P00 | P01 | P02
Local array B with block size of 3:
p,q | 0 | 1 | 2
-----|-----------------|------------------|-----------------
| 1.0 1.0 9.0 | 1.0 4.0 6.0 | 1.0 7.0 3.0
0 | 1.0 2.0 8.0 | 1.0 5.0 5.0 | 1.0 8.0 2.0
| 1.0 3.0 7.0 | 1.0 6.0 4.0 | 1.0 9.0 1.0
The value of info is 0 on all processes.
[ Top of Page | Previous Page | Next Page | Table of Contents | Index ]