Parallel Engineering and Scientific Subroutine Library for AIX Version 2 Release 3: Guide and Reference
This subroutine uses Cholesky factorization to factor a positive definite
symmetric band matrix A, stored in upper- or lower-band-packed
storage mode, into one of the following forms:
- A = UTU if
A is upper triangular.
- A = LLT if A is lower
triangular.
where, in the formulas above:
- A represents the global positive definite symmetric band
submatrix Aja:ja+n-1,
ja:ja+n-1 to be factored.
- U is an upper triangular matrix.
- L is a lower triangular matrix.
To solve the system of equations with multiple right-hand sides, follow the
call to this subroutine with one of more calls to PDPBTRS. The output
from this factorization subroutine should be used only as input to
PDPBTRS.
If n = 0, no computation is performed and the subroutine
returns after doing some parameter checking. See references [2], [23], [39], and [40].
Table 69. Data Types
| A, af, work
| Subroutine
|
| Long-precision real
| PDPBTRF
|
| Fortran
| CALL PDPBTRF (uplo, n, k, a,
ja, desc_a, af, laf, work,
lwork, info)
|
| C and C++
| pdpbtrf (uplo, n, k, a, ja,
desc_a, af, laf, work, lwork,
info);
|
- uplo
- indicates whether the upper or lower triangular part of the global
submatrix A is referenced, where:
If uplo = 'U', the upper triangular part is
referenced.
If uplo = 'L', the lower triangular part is
referenced.
Scope: global
Specified as: a single character;
uplo = 'U' or 'L'.
- n
- is the number of columns in the submatrix A, stored in upper-
or lower-band-packed storage mode, to be factored.
Scope: global
Specified as: a fullword integer;
0 <= n <= (NB_A)p-mod(ja-1,NB_A).
- k
- is the half bandwidth of the submatrix A to be factored.
Scope: global
Specified as: a fullword integer, where:
- If uplo = 'U',
0 <= k <= NB_A.
- If uplo = 'L',
0 <= k < n.
These limits for k are extensions of the ScaLAPACK
standard.
- a
- is the local part of the global positive definite symmetric band matrix
A, stored in upper- or lower-band-packed storage mode, to be
factored. This identifies the first element of the local
array A. This subroutine computes the location of the first
element of the local subarray used, based on k, ja,
desc_a, and p; therefore, the leading k+1 by
LOCp(ja+n-1) part of the local array A must
contain the local pieces of the leading k+1 by
ja+n-1 part of the global matrix, and:
- If uplo = 'U', the leading
n × n upper triangular part of the global
submatrix Aja:ja+n-1,
ja:ja+n-1 must contain the upper
triangular part of the submatrix, and the strictly lower triangular part is
not referenced.
- If uplo = 'L', the leading
n × n lower triangular part of the global
submatrix Aja:ja+n-1,
ja:ja+n-1 must contain the lower
triangular part of the submatrix, and the strictly upper triangular part is
not referenced.
Scope: local
Specified as: an LLD_A by (at least)
LOCp(ja+n-1) array, containing numbers of the data
type indicated in Table 69. Details about the block-cyclic data distribution of
global matrix A are stored in desc_a.
On output, array A is overwritten; that is, original input
is not preserved.
- ja
- is the column index of the global matrix A, identifying the
first column of the submatrix A.
Scope: global
Specified as: a fullword integer;
1 <= ja <= N_A and
ja+n-1 <= N_A.
- desc_a
- is the array descriptor for global matrix A, which may be type
501 or type 1, as described in the following tables.
| desc_a
| Name
| Description
| Limits
| Scope
|
| 1
| DTYPE_A
| Descriptor Type
| DTYPE_A = 501 for 1 × p or
p × 1
where p is the number of processes in a process grid.
| Global
|
| 2
| CTXT_A
| BLACS context
| Valid value, as returned by BLACS_GRIDINIT or BLACS_GRIDMAP
| Global
|
| 3
| N_A
| Number of columns in the global matrix
|
If n = 0:
N_A >= 0
Otherwise:
N_A >= 1
| Global
|
| 4
| NB_A
| Column block size
| NB_A >= 1 and
0 <= n <= (NB_A)p-mod(ja-1,NB_A)
| Global
|
| 5
| CSRC_A
| The process column over which the first column of the global matrix is
distributed
| 0 <= CSRC_A < p
| Global
|
| 6
| LLD_A
| Leading dimension
| LLD_A >= k+1
| Local
|
| 7
| --
| Reserved
| --
| --
|
Specified as: an array of (at least) length 7, containing fullword
integers.
| desc_a
| Name
| Description
| Limits
| Scope
|
| 1
| DTYPE_A
| Descriptor type
| DTYPE_A = 1 for 1 × p
where p is the number of processes in a process grid.
| Global
|
| 2
| CTXT_A
| BLACS context
| Valid value, as returned by BLACS_GRIDINIT or BLACS_GRIDMAP
| Global
|
| 3
| M_A
| Number of rows in the global matrix
| M_A > k
| Global
|
| 4
| N_A
| Number of columns in the global matrix
|
If n = 0:
N_A >= 0
Otherwise:
N_A >= 1
| Global
|
| 5
| MB_A
| Row block size
| MB_A >= 1
| Global
|
| 6
| NB_A
| Column block size
| NB_A >= 1 and
0 <= n <= (NB_A)p-mod(ja-1,NB_A)
| Global
|
| 7
| RSRC_A
| The process row over which the first row of the global matrix is
distributed
| RSRC_A=0
| Global
|
| 8
| CSRC_A
| The process column over which the first column of the global matrix is
distributed
| 0 <= CSRC_A < p
| Global
|
| 9
| LLD_A
| The leading dimension of the local array
| LLD_A >= k+1
| Local
|
Specified as: an array of (at least) length 9, containing fullword
integers.
- af
- is a reserved output area and its size is specified by
LAF.
Scope: local
Specified as: for migration purposes, you should specify a
one-dimensional, long-precision array of (at least) length
LAF.
- laf
- is the number of elements in array AF.
The laf argument must be specified; however, this subroutine
currently ignores its value. For migration purposes, you should specify
laf using the formula below.
Scope: local
Specified as: a fullword integer,
laf >= (NB_A+2k)(k).
- work
- has the following meaning:
If lwork = 0, work is ignored.
If lwork <> 0, work is the work area used by
this subroutine, where:
- If lwork <> -1, the size of work is (at least)
of length lwork.
- If lwork = -1, the size of work is (at least) of
length 1.
Scope: local
Specified as: an area of storage containing numbers of data type
indicated in Table 69.
- lwork
- is the number of elements in array WORK.
Scope:
- If lwork >= 0, lwork is local
- If lwork = -1, lwork is global
Specified as: a fullword integer; where:
- If lwork = 0, PDPBTRF dynamically allocates the work area
used by this subroutine. The work area is deallocated before control is
returned to the calling program. This option is an extension to the
ScaLAPACK standard. It is suggested that you specify
lwork=0.
- If lwork = -1, PDPBTRF performs a work area query and
returns the optimum required size of work in
work1. No computation is performed and the
subroutine returns after error checking is complete.
- Otherwise, it must have the following value:
lwork >= k2
- info
- See On Return.
- a
- a is the updated local part of the global matrix A,
containing the results of the factorization, where:
- If uplo = 'U', the leading
n × n upper triangular part of the global
submatrix Aja:ja+n-1,
ja:ja+n-1 contains the results of
the factorization. The remaining elements stored in submatrix
A were overwritten by this subroutine.
- If uplo = 'L', the leading
n × n lower triangular part of the global
submatrix Aja:ja+n-1,
ja:ja+n-1 contains the results of
the factorization. The remaining elements stored in submatrix
A were overwritten by this subroutine.
Scope: local
Returned as: an LLD_A by (at least)
LOCp(ja+n-1) array, containing numbers of the data
type indicated in Table 69.
On output, array A is overwritten; that is, original input
is not preserved.
- af
- is a reserved area.
- work
- is the work area used by this subroutine if lwork <> 0,
where:
If lwork <> 0 or lwork <> -1, the
size of work is (at least) of length lwork.
If lwork = -1, the size of work is (at least) of
length 1.
Scope: local
Returned as: an area of storage, containing numbers of the data type
indicated in Table 69, where:
- If lwork >= 1, work1 is set to the
minimum lwork value needed.
- If lwork = -1, work1 is set to the
optimum lwork value needed.
Except for work1, the contents of work are
overwritten on return.
- info
- has the following meaning:
If info = 0, global submatrix A is positive
definite and the factorization completed normally, or the work area query
completed successfully.
If info > 0, the leading minor of order i of
the global submatrix A is not positive definite.
info is set equal to i, where the first leading minor was
encountered at Aja+i-1,
ja+i-1. The results contained in matrix
A are not defined.
Scope: global
Returned as: a fullword integer;
info >= 0.
- In your C program, argument info must be passed by
reference.
- This subroutine accepts lowercase letters for the uplo
argument.
- This subroutine gives the best performance for wide band widths, for
example:
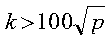
where p is the number of processes. For details, see
references [2], [39], and [40].
Also, it is suggested that you specify
uplo = 'L'.
- The k+1 by n array specified for submatrix A
must remain unchanged between calls to PDPBTRF and PDPBTRS. This
subroutine overwrites data in positions that do not contain the positive
definite symmetric band matrix A stored in upper- or
lower-band-packed storage mode.
- The output from this factorization subroutine should be used only as input
to the solve subroutine PDPBTRS.
The data specified for input arguments uplo, n, and
k must be the same for both PDPBTRF and PDPBTRS.
The matrix A and af input to PDPBTRS must be the same
as the corresponding output arguments for PDPBTRF; and thus, the scalar
data specified for ja, desc_a, and laf must also be
the same.
- In all cases, follow these rules:
- DTYPE_A=501 or 1
- If DTYPE_A=1, RSRC_A=0, M_A >= k+1, and MB_A >= 1.
- Following are the allowable array descriptor types and process grids,
where p is the number of processes in the process grid:
| DTYPE_A
| Process Grid
|
| 501
| p × 1 or 1 × p
|
| 1
| 1 × p
|
- To determine the values of LOCp(n) used in the argument
descriptions, see Determining the Number of Rows and Columns in Your Local Arrays for descriptor type-1 or Determining the Number of Rows or Columns in Your Local Arrays for descriptor type-501 and
type-502.
- Matrix A, af, and work must have no common
elements; otherwise, results are unpredictable.
- The global symmetric band matrix A must be positive
definite. If A is not positive definite, this subroutine
uses the info argument to provide information about A and
issues an error message. This differs from ScaLAPACK, which only uses
the info argument to provide information about A.
- The global positive definite symmetric band matrix A must be
stored in upper- or lower-band-packed storage mode. See the section on
block-cyclically distributing a symmetric matrix in Matrices.
Matrix A must be distributed over a one-dimensional process
grid, using block-cyclic data distribution. For more information on
using block-cyclic data distribution, see Specifying Block-Cyclically-Distributed Matrices for the Banded Linear Algebraic Equations.
- If lwork = -1 on any process, it must equal
-1 on all processes. That is, if a subset of the processes
specifies -1 for the work area size, they must all specify
-1.
- Although global matrix A may be block-cyclically distributed on
a 1 × p or p × 1 process grid,
the values of n, ja, and NB_A must be chosen so that each
process has at most one full or partial block of the global submatrix
A.
Matrix A is not positive definite. For details, see the
description of the info argument.
lwork= 0 and unable to allocate workspace
Stage 1:
- DTYPE_A is invalid.
Stage 2:
- CTXT_A is invalid.
Stage 3:
- PDPBTRF was called from outside the process grid.
Stage 4:
- The process grid is not 1 × p or
p × 1.
- uplo <> 'U' or 'L'
- n < 0
- ja < 1
- k < 0
- k+1 > n
- DTYPE_A = 1 and:
- M_A < k+1
- MB_A < 1
- RSRC_A <> 0
- The process grid is not 1 × p.
- N_A < 0 and (n = 0); N_A < 1
otherwise
- NB_A < 1
- n > (NB_A)p-mod(ja-1,NB_A)
- CSRC_A < 0 or CSRC_A >= p
- uplo = 'U' and
k > NB_A.
Stage 5:
- ja > N_A and (n > 0)
- ja+n-1 > N_A and
(n > 0)
- LLD_A < k+1
Stage 6:
- lwork <> 0, lwork <> -1, and
lwork < k2
Stage 7:
Each of the following global input arguments are checked to determine
whether its value differs from the value specified on process
P00:
- uplo differs.
- n differs.
- k differs.
- ja differs.
- DTYPE_A differs.
- DTYPE_A does not differ and:
- N_A differs.
- NB_A differs.
- CSRC_A differs.
- DTYPE_A = 1 and:
- M_A differs.
- MB_A differs.
- RSRC_A differs.
Also:
- lwork = -1 on a subset of processes.
This example shows a factorization of the positive definite symmetric band
matrix A of order 9 with a half bandwidth of 7:
* *
| 1.0 1.0 1.0 1.0 1.0 1.0 1.0 1.0 0.0 |
| 1.0 2.0 2.0 2.0 2.0 2.0 2.0 2.0 1.0 |
| 1.0 2.0 3.0 3.0 3.0 3.0 3.0 3.0 2.0 |
| 1.0 2.0 3.0 4.0 4.0 4.0 4.0 4.0 3.0 |
| 1.0 2.0 3.0 4.0 5.0 5.0 5.0 5.0 4.0 |
| 1.0 2.0 3.0 4.0 5.0 6.0 6.0 6.0 5.0 |
| 1.0 2.0 3.0 4.0 5.0 6.0 7.0 7.0 6.0 |
| 1.0 2.0 3.0 4.0 5.0 6.0 7.0 8.0 7.0 |
| 0.0 1.0 2.0 3.0 4.0 5.0 6.0 7.0 8.0 |
* *
Matrix A is stored in lower-band-packed storage mode:
* *
| 1.0 2.0 3.0 4.0 5.0 6.0 7.0 8.0 8.0 |
| 1.0 2.0 3.0 4.0 5.0 6.0 7.0 7.0 . |
| 1.0 2.0 3.0 4.0 5.0 6.0 6.0 . . |
| 1.0 2.0 3.0 4.0 5.0 5.0 . . . |
| 1.0 2.0 3.0 4.0 4.0 . . . . |
| 1.0 2.0 3.0 3.0 . . . . . |
| 1.0 2.0 2.0 . . . . . . |
| 1.0 1.0 . . . . . . . |
* *
where "." means you do not have to store a value in that
position in the local array. However, these storage positions are
required and are overwritten during the computation.
Matrix A is distributed over a 1 × 3 process grid
using block-cyclic distribution.
Notes:
- Matrix A, output from PDPBTRF, must be passed, unchanged, to
the solve subroutine PDPBTRS.
- The laf argument must be specified; however, this subroutine
currently ignores its value. For migration purposes, in this example,
laf is specified as 119.
- The af argument is reserved and not shown in this example.
- Because lwork = 0, PDPBTRF dynamically allocates the work
area used by this subroutine.
ORDER = 'R'
NPROW = 1
NPCOL = 3
CALL BLACS_GET (0, 0, ICONTXT)
CALL BLACS_GRIDINIT(ICONTXT, ORDER, NPROW, NPCOL)
CALL BLACS_GRIDINFO(ICONTXT, NPROW, NPCOL, MYROW, MYCOL)
UPLO N K A JA DESC_A AF LAF WORK LWORK INFO
| | | | | | | | | | |
CALL PDPBTRF( 'L' , 9 , 7 , A , 1 , DESC_A , AF , 119 , WORK , 0 , INFO )
| Desc_A
|
| DTYPE_
| 501
|
| CTXT_
| icontxt(CGBTOO9)
|
| N_
| 9
|
| NB_
| 3
|
| CSRC_
| 0
|
| LLD_A
| 8
|
| Reserved
| --
|
|
Notes:
- icontxt is the output of the BLACS_GRIDINIT
call.
|
Global matrix A stored in lower-band-packed storage mode with
block size of 3:
B,D 0 1 2
* *
| 1.0 2.0 3.0 | 4.0 5.0 6.0 | 7.0 8.0 8.0 |
| 1.0 2.0 3.0 | 4.0 5.0 6.0 | 7.0 7.0 . |
| 1.0 2.0 3.0 | 4.0 5.0 6.0 | 6.0 . . |
| 1.0 2.0 3.0 | 4.0 5.0 5.0 | . . . |
0 | 1.0 2.0 3.0 | 4.0 4.0 . | . . . |
| 1.0 2.0 3.0 | 3.0 . . | . . . |
| 1.0 2.0 2.0 | . . . | . . . |
| 1.0 1.0 . | . . . | . . . |
* *
The following is the 1 × 3 process grid:
B,D | 0 | 1 | 2
-----| ------- | ------- |-------
0 | P00 | P01 | P02
Local array A with block size of 3:
p,q | 0 | 1 | 2
-----|-----------------|------------------|-----------------
| 1.0 2.0 3.0 | 4.0 5.0 6.0 | 7.0 8.0 8.0
| 1.0 2.0 3.0 | 4.0 5.0 6.0 | 7.0 7.0 .
| 1.0 2.0 3.0 | 4.0 5.0 6.0 | 6.0 . .
| 1.0 2.0 3.0 | 4.0 5.0 5.0 | . . .
0 | 1.0 2.0 3.0 | 4.0 4.0 . | . . .
| 1.0 2.0 3.0 | 3.0 . . | . . .
| 1.0 2.0 2.0 | . . . | . . .
| 1.0 1.0 . | . . . | . . .
Output:
Global matrix A is returned in lower-band-packed storage mode
with block size of 3:
B,D 0 1 2
* *
| 1.0 1.0 1.0 | 1.0 1.0 1.0 | 1.0 1.0 1.0 |
| 1.0 1.0 1.0 | 1.0 1.0 1.0 | 1.0 1.0 . |
| 1.0 1.0 1.0 | 1.0 1.0 1.0 | 1.0 . . |
| 1.0 1.0 1.0 | 1.0 1.0 1.0 | . . . |
0 | 1.0 1.0 1.0 | 1.0 1.0 . | . . . |
| 1.0 1.0 1.0 | 1.0 . . | . . . |
| 1.0 1.0 1.0 | . . . | . . . |
| 1.0 1.0 . | . . . | . . . |
* *
The following is the 1 × 3 process grid:
B,D | 0 | 1 | 2
-----| ------- | ------- |-------
0 | P00 | P01 | P02
Local array A with block size of 3:
p,q | 0 | 1 | 2
-----|-----------------|------------------|-----------------
| 1.0 1.0 1.0 | 1.0 1.0 1.0 | 1.0 1.0 1.0
| 1.0 1.0 1.0 | 1.0 1.0 1.0 | 1.0 1.0 .
| 1.0 1.0 1.0 | 1.0 1.0 1.0 | 1.0 . .
| 1.0 1.0 1.0 | 1.0 1.0 1.0 | . . .
0 | 1.0 1.0 1.0 | 1.0 1.0 . | . . .
| 1.0 1.0 1.0 | 1.0 . . | . . .
| 1.0 1.0 1.0 | . . . | . . .
| 1.0 1.0 . | . . . | . . .
The value of info is 0 on all processes.
[ Top of Page | Previous Page | Next Page | Table of Contents | Index ]